Theoretical Explanation.

Our story starts with Évariste Galois (1811-1832) who founded the theory based on the symmetries of permutations which we now know as group theory. The original explanation of Woodward and Hoffmann based on the nature of the highest occupied molecular orbitals was formalised with the help of Galois' group theory by Longuet-Higgins and Abrahamson (DOI: 10.1021/ja01087a033, see also 10.1021/ja01087a033). This involved generating a so called orbital correlation diagram for the reaction under consideration, and then carrying out the reaction in such a manner that the group theoretical symmetries of the reactant and product orbitals matched exactly. Such an approach, whilst theoretically more rigorous, is not readily applicable to the majority of more complex reactions which have no formal symmetry. Two much simpler methods have been subsequently outlined which avoid this problem. The first these, based on transition state aromaticity, will be expanded in more detail, whilst the second (based on frontier orbitals) will only be described briefly at the end of this lecture.

1. Conservation of Orbital Symmetry (Longuet-Higgins and Abrahamson)

Let us first define the symmetry properties of a 1s and a 2p orbital with respect to a plane of symmetry or an axis of symmetry as shown below;

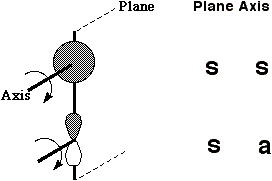
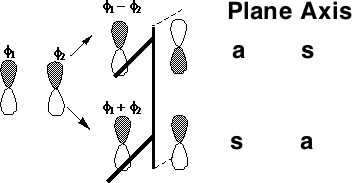
One can take this one step further by considering the symmetry properties of molecular orbitals formed by the overlap of two or more atomic orbitals;

MOs formed from two overlapping σ orbitals:

MOs formed from two overlapping p-orbitals (σ bonds):

MOs formed from two parallel overlapping p-orbitals (π bonds):

We can now use these basic orbitals to construct the relevant molecular orbitals for two interconverting molecules, cyclobutene and butadiene, with the purpose of following how these two sets of orbitals change when one molecule is converted into the other. Note particularly that we need only construct the MOs explicitly involved in the reaction; most of the σ framework remains unchanged and no orbitals derived from this need to be considered:

---

Conrotation:

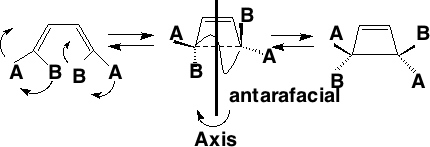
Disrotation:

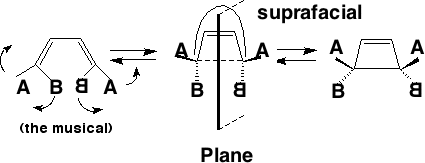
This enables a correlation diagram for the reaction to be constructed, according to the following rules: no two orbitals of the same symmetry can cross during the reaction, whilst orbitals of different symmetry can cross. The favoured pathway is the one which results in a product of the same electronic excitation as the reactant (green).

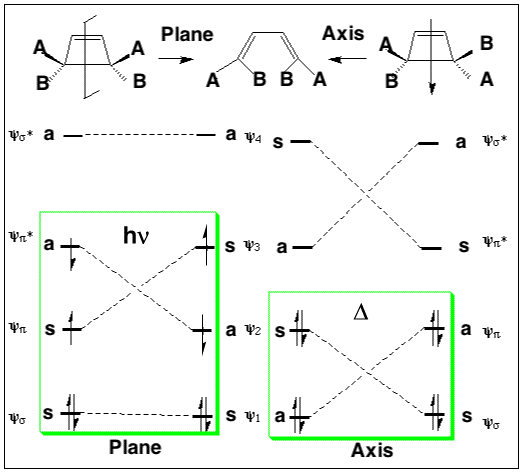
Pathways which result in the product being formed in a higher electronic state than the reactant are said to be "forbidden" (red).

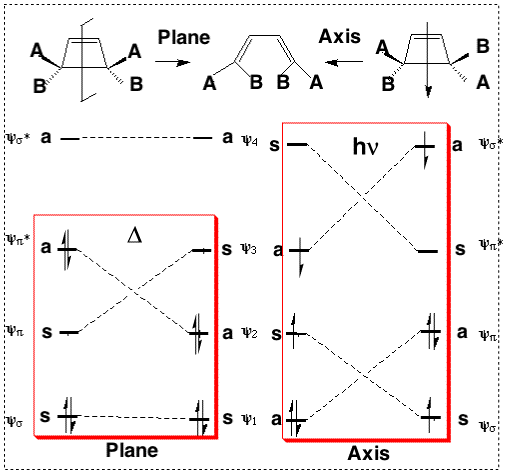
Whilst this rule is normally followed fairly well for ground states, it can be overturned when for example steric or geometrical strain in the "allowed" pathway promotes the "forbidden" route. The situation is actually more complex for photochemical reactions, and much recent evidence suggests that the Woodward-Hoffmann rules are not always followed. These correlation diagrams can be generalised for any electrocyclic reaction with appropriate symmetry. However, correlation diagrams are less readily applied for reactions with no symmetry. Dewar and Zimmerman independently noticed that the 'topological' properties of these correlation diagrams are very similar to those obtained using eg Hückel theory for aromatic molecules. For example, the diagram for the electrocyclic conversion of hexatriene to cyclohexadiene is remarkably similar at the transition state to the ground state orbitals of benzene;

2. Alternative Approach: Transition State Aromaticity (Dewar and Zimmermann)

2.2. Möbius Aromatics (Heilbronner) The antarafacial mode described above is said to resemble "Möbius" topology, after August Ferdinand Möbius, who invented the famous strips (as did Johann Benedict Listing). An antarafacial mode can be formed by taking a cyclic alkene "strip" and giving its π-electron system a 180° (half) twist (and in doing create a two-fold axis of symmetry in the resulting molecule). Edgar Heilbronner in 1964 worked out that such a twisted system would be a closed shell molecule (later shown to be also aromatic) if it contained 4n conjugated π electrons. The first explicit example of such a molecule was suggested in 1998, for the molecule C9H9+ (which has 8 cyclically conjugated π-electrons and is a 4n system, where n=2). It has π-orbitals that have quite different features from those of benzene. It is now recognized (DOI: 10.1039/b810301a) that the orbitals in such a system cannot be considered singly, but must be regarded in pairs. A topological analysis of such a pair results in an object known as a torus knot, which corresponds to a cyclically continuous band of electron density making two complete cycles of the ring, with a linking number of one (the specific name of the knot here is actually unknot) and which exhibits dissymetric chirality. In 2003, a crystalline Mobius annulene was first made (DOI: 10.1021/cr030092l) and quite a number of Mobius systems have been identified from 2006 onwards. Just as with excited state Hückel aromatics, Möbius molecules in the excited (actually triplet) state are also thought to be aromatic if they contain 4n+2 rather than 4n π electrons. An article describing the above concepts in greater detail is available here.

These four types of aromaticity are most easily summarised by selection rules.

Another useful mnemonic for remembering the basic rules is due to Frost, Musulin and Zimmermann, formulated in this form in 1965:

3. Alternative Approach: The Frontier Orbital Method (Fukui)

(The following is optional and is intended for use in tutorials). This involves using the principles of quantum mechanics to generate the Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO) for the reactant(s). The formation of the new σ bond must occur by appropriate overlap of the nodes of these orbitals. If only one σ bond is forming, as in an electrocyclic reaction, then only the overlap of the HOMO of the reactant is considered. Such overlap can occur in one of two fundamental ways; The suprafacial mode involves each component of the new σ bond being formed from the SAME face of the reactant π system. See DOI: 10.1016/S0040-4039(01)83901-0.

The antarafacial mode involves a 'twisting' of the orbitals so that the two components of the new σ bond come from OPPOSITE faces of the reactant π system. If two or more σ bonds form during the reaction, as in cycloaddition reactions, then the overlap of the HOMO of one reactant with the LUMO of the second reactant must be considered. For simple systems, the form of the HOMO and LUMO is not difficult to remember. For more complex systems, explicit calculations have to be carried out and the Frontier Orbital method becomes more difficult to apply. The advantage of the "FMO" method is that it can be expressed quantitatively in terms of the magnitude of the coefficients involved, and can hence be used to predict regioselectivity etc.

4. Modern Approach: The Transition State Potential Energy Surface Method