Techniques of Molecular Modelling: Quantum Mechanical Methods
Molecular orbital methods date back to the origins of quantum mechanics and the Schrödinger equation.
- The first practical chemical solution to this equation was formulated by Erich Hückel in 1931 and dealt exclusively with planar conjugated systems.
- This molecular orbital theory was thereafter extended by Pauling, Hartree and Fock, Mulliken and many others,
- and first effectively implemented in the 1960s by Hoffmann and Lipscomb to all valence electron systems (EHT),
- by Pople in the 1970s who defined a family of semi-empirical methods
- which were first effectively paramterised by Dewar (MINDO/3, MNDO, AM1), Stewart PM3 and 6)
- In parallel, effective implementations of ab initio and density functional methods emerged in the 1980s (Gaussian, GAMESS, Turbomole, Orca, etc)
In essence, QM methods differ from the MM methods in providing explicit solutions for the electronic component of a molecule rather than just the nuclear terms.
These methods all adopt the Born-Oppenheimer approximation. Stated approximately, we assume that the motion and (point) position of the nuclei is described by classical equations, whereas the electrons is described by non-classical wavefunctions. This means the nuclear-nuclear energy contributions are classical mechanical (electrostatic point charge), but the nuclear-electron and electron-electron terms are quantum mechanical and the total energy is the sum of these nuclear and electronic components. The starting point for solving the electronic part is the Schrödinger equation:
H.Ψ = E.Ψ
| Methods which integrate Hamiltonian (H) and Basis set (Ψ) |
- AM1 (Austin Model 1, based on a parametrised Hartree-Fock model), a Semiempirical method parametrised for ~42 elements. The method uses only valence shell atomic orbitals, representing them with Slater functions (see below), whilst the inner shells (e.g. 1s for C) and other terms in the Hartree-Fock equations are modelled with parametric functions (often referred to as the NDDO set of approximations) in a manner similar to molecular mechanics.
- PM3, a reparametrisation of AM1, introduced in 1989 and a bit like the curate's egg (much better for e.g. H-bonding). Parameters for 42 elements in all combinations.
- PM6, a reparametrisation of PM3 introduced in 2007 and about twice as accurate. Includes parameters for 69 elements (but not necessarily all possible combinations) DOI: 10.1007/s00894-007-0233-4. In 2009, the method was extended with explicit terms for dispersion energies (van der Waals) and delocalized hydrogen bonds, PM6-DH2+.
- RM1 is the latest (2008) method in this stable, offering high accuracy parameters for all combinations of the 10 most common elements (H, C, N, O, P, S, F, Cl, Br, I).
- Oniom: A method first introduced in 1996 which partitions a molecule into layers, each treated using a different approximation. The most common is a two layer model, the outer layer treated using molecular mechanics (or even a simpler unified field model), the inner one treated using MO theories. Three layer models apply one of mechanics, one of semi-empirical and one of ab initio MO theories (DOI: 10.1021/jp962071j)
|
| Η: List of Ab initio/Density functional Hamiltonians |
Ψ: List of Basis sets |
- RHF, or (Spin) Restricted Hartree Fock. Applied to singlet electronic states (all electrons paired) and used for relatively rapid prototyping of a calculation. No consideration for electron correlation.
- UHF, or (Spin) Unrestricted Hartree Fock, for use with open shell systems (doublets, triplets, etc).
- ROHF. Restricted openshell Hartree Fock, for open shell systems. More limited than UHF for some systems (ie 2nd derivatives, etc) but free of spin contamination.
- B3LYP (UB3LYP): A popular density functional method (not strictly an ab initio one), offering good reliability and short range electron correlation treatment at the penalty of about half the speed of a RHF calculation. There are many other functionals that have been proposed, but none tested so thoroughly as this one.
- wB97XD (Density functional theory with empirical long-range correlation correction; DOI: 10.1039/b615319b). These dispersion corrections have been incorporated into new generations of double-hybrid methods, such as BML and B2-PLYP/B2GP-PLYP which address many deficiencies of B3LYP (DOI: 10.1021/jp710179r) and which occupy the so-called fifth rung of Jacob's ladder of approximations (DOI: 10.1063/1.1390175)
- MP2 (MP4), Moller-Plesset methods based on perturbation theory, an older method than the density functionals for incorporating electron correlation. Perhaps 10-100 times slower than HF, but in some cases more reliable, especially for so-called "long range correlation effects". New double-hybrid DFT methods rely on MP2 for the correlation part of the DFT functional.
- CISD; Configuration Interaction based on a Hartree-fock reference state, for systems where multiple electronic configurations and electron correlation are important, e.g. excited states etc.
- CASSCF(n,n); a keyword for invoking multi-configurational SCF where the Hartree-Fock reference state is simply not good enough (i.e. transition metal series, excited states, etc).
- CCSD(T), CCSDTQ; the so-called coupled-cluster approach to the correlation problem. Very very expensive, and can only be properly applied to about 10-12 (non-hydrogen) atoms.
|
- STO-3G. A minimal (single-ζ) basis set. Use for very rapid prototyping of a calculation, or initial geometry optimisation from a poor starting guess. The 3 means using three Gaussian-type functions sharing a common exponent (ζ) to represent a shell (modelled on the Slater-type-function or STO, this being adapted from the Schrödinger solutions for a hydrogen atom).
- 3-21G*. a small double-ζ basis set due to Pople, and available for most of the periodic table. The 3 is used for the core electrons (1s for eg carbon), the "2" and "1" are used for the valence electrons, and are represented by respectively two and one Gaussian functions, each with its own ζ exponent. The "*" means polarization (d) functions on e.g. S, P, Cl etc. Used for relatively rapid prototyping of a calculation.
- SDD, an alternative basis set for the entire period table using effective core potentials (Pseudopotentials) to reduce the number of basis functions (for the core electrons) and to include relativistic effects (for heavy elements).
- 6-31+(d,p). A reasonably high quality double-ζ basis set with anionic diffuse (+) and "polarisation functions" on the atoms ("p" orbital for Hydrogen, "d and f" orbital for carbon, "f and g" orbital for transition metals, etc).
- cc-pVTZ. A triple-ζ correlation-consistent basis set with valence polarization functions, now regarded as appropriate for reasonably high quality on small to medium sized molecules.
- aug-cc-pV5Z and aug-cc-pV5Z-pp. An augmented and polarized "pentuple ζ", correlation-consistent basis set for best quality calculations; available significantly for the first transition series. The higher elements are treated using pseudopotentials (pp). Also included in this type of basis is the aug-pcx (x=1-4) Kohn-Sham consistent basis for use on the fifth rung of Jacob's ladder.
- Gen: A general input for basis sets. Get them from here and mix-n-match your basis sets for the problem at hand.
|
| Methods which extrapolate Hamiltonian and Basis set |
- G2/G3 (Gaussian-3): Effectively an extrapolation of both the basis set, and the correlation treatment, the combination of which heads off towards exact solutions of the Schrödinger equation. Hugely expensive in computer time.
- W1-W4 Theories, currently considered the most accurate solutions to the Schrödinger equations available. This level of theory is now routinely correcting "faulty" experimental data! See DOI: 10.1063/1.2348881, 10.1021/jp071690x, 10.1021/jp900056w and 10.1063/1.3489113
|
How the various methods scale with size: Let us define N as ~ the number of atoms (slightly more accurately, it represents the number of basis functions associated with all the atoms in the molecule under consideration, and so it also goes up with the quality of the basis set)
- Methods which do not require 2-electron integral evaluations scale as N2 (due entirely to diagonalising the Hamiltonian (Fock) matrix, but this only kicks in for very large matrices)
- Semi-empirical methods ~ N2 (but can be made to scale as N1 for larger molecules, say > 500 atoms)
- DFT methods ~N3-N4
- MP2 methods ~N5-N6
- Coupled cluster methods, ~N6-N8
One also has to consider how the 1st and 2nd derivatives of the energy with respect to the nuclear coordinates behave. The most recent implementations of density functional theory have low scaling 1st and 2nd analytical derivatives, which now routinely enable good geometry optimisations using BFGS-like algorithms.
There are two ways of approaching this problem. The simplest is to look at either the properties of the reactant, or the properties of the initial product, the Wheland intermediate. We will look at the first of these initially.
-
The Properties of the Reactant: A substituted Benzene.
Henry Armstrong, working at (the precursor to) Imperial College around 1887, was one of the first chemists to categorise substituents (R, or Radicles as he calls them) on a benzene ring in terms of the effect they had towards electrophilic substitution reactions (of X) of the ring. With the electron yet to be discovered, he attributed the two observed modes of behaviour (i.e. o/p in Table I vs m in Table II of 10.1039/CT8875100258) as being due to an electrically polarizable entity he called an "affinity", of which he suggested a benzene ring had six. He also suggested these affinities acted at a distance over the whole ring, but which differed in their directionality (or Resultant as he puts it, the modern term for which is Vector) according to the nature of R (a difference we nowadays categorize as being the electron donating or withdrawing properties of R). Armstrong's description of the properties of his affinity (See DOI: 10.1039/CT8875100258 where he writes "the introduction of a radical/substituent [onto the benzene ring] doubtless involves an altered distribution of the affinity, much as the distribution of the electric charge in a body is altered by bringing it near to another body". In 10.1039/PL8900600095, p102, he also clearly describes what we now know as a Wheland intermediate) may well constitute the first glimmering of the wave-like properties of the electron!
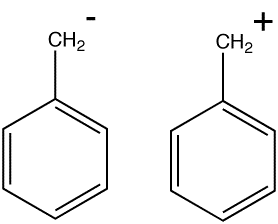
Erich Hückel some 44 years later was able to derive from Schrödinger's wave equation a simple expression which predicted how these "affinities", now named electrons of course, could be polarized. The resulting (π) molecular orbital functions (eigenvectors) can be used to illustrate graphically how both the directing effects (i.e. the probability of finding electrons in any particular position, i.e. the MOs) and the activating/deactivating effects (i.e. the probability of interacting with the electrons, i.e. the orbital energies) operate.
To maximise the visual effect, we are going to use two substituents R that were not in fact in Armstrong's original list; CH2+ for an electron withdrawing group and CH2- for an electron donating group. Its worth considering just for a moment why we are not using more conventional neutral groups (i.e. NO2 and NH2 respectively) for this illustration. Being neutral, the latter groups can only polarize the molecule by separating charge to produce a dipolar ionic species. Such ionic charge separation always takes a fair bit of energy to achieve compared to neutral covalent bonding, and actually requires proper solvation to treat quantitatively. It is much easier if the R group is already ionic, because then moving the charge from one part of the molecule to another takes little energy and no change in ionicity, and hence eliminates the need for any solvation treatment.
| o/p Directing |
m-Directing |
| HOMO, R=CH2- |
HOMO, R=CH2+ |
HOMO-1, R=CH2+ |
|
|
|
|
The Highest occupied π canonical Molecular orbital (HOMO) for R=CH2- corresponds to the electron-pair least bound to the molecule and is hence the most available to react with an Electrophile. It has an energy of -1.7eV, which shows how relatively weakly it is bound (most π electrons have energies around -10ev or even less). This weak binding is also associated with it being a good nucleophile. Note how this wavefunction has density on the ortho and the para positions of the ring, but none at all on the meta position. This of course matches the resonance bond formulation familiar to all organic chemists, and hence the recognition of o/p direction and activation for such a substituent.
Contrast this with R=CH2+. The HOMO in this case has an energy of -15.0eV, very much more tightly bound, with hence with vastly reduced nucleophilic properties. It has a node in the para position. The next highest orbital is almost degenerate with the HOMO (-15.6 eV) and has a node in the ortho positions. Because these two orbitals are essentially the same in energy, they have to be considered together; the only position where both of them do have density is in the meta position. This substituent therefore is meta directing, but strongly deactivating (due to the very negative orbital energies).
If we now assume that the reactant has similar properties to the transition state for this reaction (the Hammond principle, in part) we can infer that the transition state will inherit the same properties, and that the electrophilic reactivity of such substituted benzene derivatives can be derived purely from the properties of the reactant (if its an early transition state)
-
The Properties of a Heterocycle: Pyridine.
What about a real system? The differing behaviour of Pyridine and its N-Oxide towards electrophilic substitution is well known. In particular, these two, apparently almost identical species, have quite different properties when nitrated. The former nitrates (albeit slowly) in the 3-position, whilst the latter nitrates (rather faster) in the 4-position. Does the HOMO for each reflect this? The answer is that the corresponding orbitals look very similar to the ones shown above! Inded, the size of the orbital at the 4-position even looks larger than that at the 2-position.
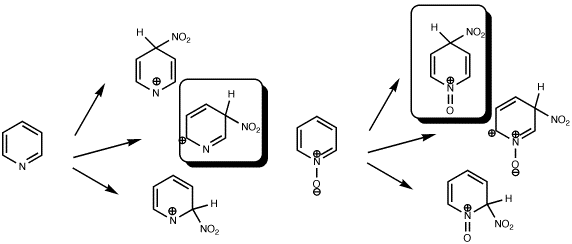
| HOMO, Pyridine, m-directing |
HOMO, Pyridine N-Oxide, o/p directing |
|
|
|
-
Properties of the Wheland/Armstrong Intermediate.
An prequel to looking at reactivity of aromatics is to consider the relative energy of the possible Wheland intermediates as being better indicators of the outcome of the reaction than simply the wavefunction of the reactant. How can one calculate the relative energies? The mechanics method, since in general the force field constants do not cancel out for the various pararmeters, is going to give a very unreliable relative energy. It will also not reflect on the polarization of the π-electrons as illustrated above. Only proper treatment of the electrons via quantum mechanics can treat this sort of problem. The energies shown below have been obtained from the PM6 semi-empirical method (which calculates the energies and optimizes the geometries of the protonated Wheland intermediate in just a few seconds). The outcome shows clearly the differentiation between Pyridine and its N-oxide, and also reproduces the preference for 4- rather than 2-substitution in the latter (But see DOI: 10.1039/P29750000277 where an argument is presented for 4-nitration resulting not by reaction of the free N-oxide but the protonated species).
| Substrate, X |
ortho (Relative to para) |
meta (Relative to para) |
para |
| Pyridine, X=N |
-3.9 (234.6) |
-15.1 (223.4) |
0.0 (238.5) |
| Pyridine N-Oxide, X=NO |
4.8 (208.9) |
25.6 (231.2) |
0.0 (205.6) |
| X=NS |
3.3 (232.4) |
23.5 (251.1) |
0.0 (227.6) |
| Phosphabenzene X=P |
0.1 (210.7) |
0.0 (210.6) |
0.0 (210.6) |
| Phosphabenzene P-oxide, X=PO |
1.7 (145.4) |
45.1 (188.8) |
0.0 (143.7) |
| X=PS |
2.2 (170.7) |
45.1 (213.6) |
0.0 (168.5) |
| Arsabenzene X=As |
3.6 (229.6) |
19.6 (245.6) |
0.0 (226.0) |
| Iridiabenzene X=Ir(PH3)3 |
3.4 |
39.4 |
0.0 |
What about other substituents? An almost entirely unstudied problem is the electrophilic substitution of
phosphabenzene. It's a great surprise to find that in modelling terms at least, it behaves
quite differently to pyridine! Using this approach, one can even predict reactivity for something as unconventional
as metallabenzenes (for a review of the chemistry of metallabenzenes, s
ee 10.1039/b517928a).
For examples of such metallabenzenes with or
. For details of the bonding in the Ru system, see this blog post.
|
|
As a visualisation problem, viewing the Crystal structure of the Pirkle reagent provided a rationalisation of how the intermolecular interactions might proceed via a novel form of hydrogen bonding involving an entire face of one aromatic ring. We saw how Molecular mechanics is not parameterised to deal with such an unusual interaction, and so might not handle it properly. Clearly, the location of the electrons is critical, since the H+ binds to regions of high electron density. There are three aromatic rings to choose from in this molecule, and moreover, because of the chiral centre present, two faces to each ring, ie six possibilities in all. Can calculating the wavefunction of this molecule cast light on this?
|
Part 1: The π-electrons. One solution of the Schrödinger equation provides a canonical set of energy levels for electron (pairs) in the molecule, that having the highest energy being referred to as the HOMO (Highest occupied molecular orbital). As we saw before, the HOMO corresponds to the electron (pair) which is least strongly bound to the molecule, and hence can be regarded as describing where the most basic (= proton seeking) or nucleophilic (= nucleus seeking) electrons in the molecule are. So a good first start to understand where a hydrogen bond might occur is to plot the HOMO for the Pirkle reagent. Unfortunately, the HOMO is a π type orbital and shows almost no discrimination for binding to a proton!
|
|
Part 2: The integrated σ- and π-electrons. In fact the effect we are seeking is actually transmitted via the σ framework (originating in the inductive effect of the C-F bonds) and not the π system. The next level of approximation is to recognise that the basicity of a molecule derives from not just a single MO, but a suitably weighted sum of the contributions of all the electrons, and particularly of the σ bonds. This function is called the molecular electrostatic potential or MEP. This is a workfunction, and represents the amount of energy needed to remove a bare proton from any specified position close to a molecule out to an infinite distance away. If this energy is positive, the proton was clearly bound to the molecule, if the energy is negative, it was clearly repelled by the molecule. The function needs to be computed for all points in space around the molecule, and it is conventional to calculate an "iso-value surface", or actually two iso-surfaces, one representing a positive value of the MEP, the other a negative value. This is then rendered using computer graphics. In this display the negative potential which in effect attracts a proton (i.e. give rise to a positive work function) is rendered in purple. |
Notice how the two faces of the anthracene ring are quite different, an effect induced by the electron withdrawing effect of the C-CF3 group which withdraws electrons anti-periplanar to the bond, i.e. on the face opposite to it. But in turn the lone pair of the oxygen atom re-focuses density on to one ring of this opposite face, and in fact the hydrogen bond forms at almost exactly the centre of this electron density. Thus this hydrogen bond is created by a complex stereo-electronic effect caused by the shaping of the electron density by one withdrawing group and one lone pair.
Part 3: The electron Topology (AIM or Atoms in Molecules). What happens when one places two of these molecules into the close proximity found in the crystal structure? The π-MOs are of little help, and the electrostatic potentials of the two components, as used above, interfere to the point of not really revealing anything. Yet another way of analyzing where the electrons are is needed. This is found in a technique known as Quantum Chemical Topology. It is the study of the topology of electron density in molecules, and uses the language of dynamical systems (critical points, manifolds, gradient vector fields etc, first introduced by the mathematician Henri Poincare) to identify key points in the electron densities.
There are precisely four types of points, differing in the characteristics of the curvature of the electron density ρ(r) in the region of the critical point. This curvature is obtained from the second derivative of the electron density with respect to cartesian space (the density Hessian). The eigenvalues of this 3 by 3 matrix can have exactly four conditions, which are summarised by the signature of this matrix, being the sum of the signs of these eigenvalues:
- NCP: A critical point (all three eigenvalues -ve) which identifies where an attractor (i.e. a nucleus) is in a molecule
- BCP: A critical point (two -ve, one +ve) which identifies bonds in a molecule. Normally found between a pair of attractors, but can also involve three attractors (a 3-centre bond).
- RCP: A critical point (one -ve, two +ve) which identifies rings in a molecule
- CCP: A critical point (all three eigenvalues -+ve) which identifies cages in molecules
- The total number of these various points must satisfy a topological relationship known as the Poincaré-Hopf condition, which states that num(NCP-BCP+RCP-CCP) = 1.
- One property is known as the Laplacian of the electron density, ∇2ρ(r) (being the sum of the diagonal elements of the density Hessian) at a BCP is used to characterise the type of bond in that region
- Covalent, ∇2ρ(r) negative, ρ(r) large (> 0.2)
- Ionic, ρ(r) small
- Charge shift, ∇2ρ(r) positive, ρ(r) large (> 0.2)
The most relevant of the critical points is the second type; a BCP. It tells us in effect if a bond exists between any pair of nuclei. What it does not tell is is what the bond order of that bond is; it could easily for example be less than 1. That is a chemical rather than a topological interpretation.
What happens when such an analysis is conducted on the dimer of the Pirkle reagent? In the resulting analysis (left), the light blue points are the positions of some of the critical bond points identified in the electron density topology (there are many more than shown here). These reveal some fascinating insights into how the Pirkle reagent binds with itself.
| The QTAIM Critical point analysis |
|---|
|
|
- There is indeed a bond critical point between the H of the OH group, and the π-face of one ring. It shows it binding to approximately three atoms of that ring, in exactly the manner first revealed by visualisation, and then by the MEP plot above. The electron density at this point (0.013 - 0.015 au) corresponds very approximately to an interaction energy of about 2.5 - 3.0 kcal/mol.
- A set of four bond critical points occur between four pairs of atoms in the π-π- stacked anthracene rings, with densities of around 0.004 - 0.005 au. This reveals that such stacking is indeed (weakly) attractive and of significance (totalling around 3 kcal/mol).
- A further pair of bond points is shown between the oxygen lone pair and the adjacent ring C-H bond; the density (0.018) indicates each to be worth about 3 kcal/mol.
- Thus the OH group actually participates in two concurrent types of hydrogen bonding, one to a π-face via the H, and one to a C-H bond via the lone pair. This last interaction was not spotted in this molecule until this topological analysis was done! It also re-inforces the concept that these interactions are co-operative rather than independent.
|
| The NCI Method: Surface based on (reduced) density gradient ∇ρ(r); surface colour based on ∇2ρ(r) |
|
|
- red =strongly repulsive
- yellow = weakly repulsive
- green = weakly attractive
- blue= strongly attractive.
- For more explanation, see this summary.
|
The very recent NCI (non covalent interactions) method takes this analysis one step further by developing the concept of surfaces of interaction rather than just critical points. These surfaces are derived from the density gradient ∇ρ(r) (the deviation from a homogenous electron distribution), coloured by the value of the λ2 eigenvalue of the Laplacian of the density ∇2ρ(r). The NCI method is showing great promise for explaing e.g. stereoselectivity in chemical reactions.
Part 4: Energies again. Our analysis of the Pirkle reagent concludes here with a revisitation of the binding energy. We saw previously how this could be estimated using Molecular Mechanics. This had the advantage of including the so called dispersion, or long range correlation effects, but the disadvantage that there was no ready access to the entropy of the process. A very new procedure which incorporates both advantages is the dispersion-corrected density functional method, one very recent implementation of which is ωB97XD (DOI: 10.1039/b810189b), and this gives the following values:
ΔH dimerisation -25.1; ΔS -49.2, TΔS = -14.7; ΔG dimerisation -10.4 kcal/mol.
 We (think we) know where covalent σ-bonds are in molecules, they lie along the straight line connecting the nuclei of two atoms. We can idealize lone pairs on atoms such as oxygen, and in case study 1, all we needed was an (X-ray) structure to spot a connection between the (antiperiplanar) orientation of (certain) such idealized lone pairs and the C-O bonds in the molecule. But are the lone pairs really where we have idealized them? And in dealing the orientation of the lone pair with a σ-bond, we become aware that we are actually dealing with a concept derived from the Klopman-Salem equation, which uses not so much the two-electron σ-bond, as a vacant orbital occupying the (assumed) same orientation known as the σ*-bond. This was the basis of the earlier lecture course on stereo-electronics and also conformational analysis. It is time to take some of these concepts and show how they can be properly quantified. Let us proceed as follows:
We (think we) know where covalent σ-bonds are in molecules, they lie along the straight line connecting the nuclei of two atoms. We can idealize lone pairs on atoms such as oxygen, and in case study 1, all we needed was an (X-ray) structure to spot a connection between the (antiperiplanar) orientation of (certain) such idealized lone pairs and the C-O bonds in the molecule. But are the lone pairs really where we have idealized them? And in dealing the orientation of the lone pair with a σ-bond, we become aware that we are actually dealing with a concept derived from the Klopman-Salem equation, which uses not so much the two-electron σ-bond, as a vacant orbital occupying the (assumed) same orientation known as the σ*-bond. This was the basis of the earlier lecture course on stereo-electronics and also conformational analysis. It is time to take some of these concepts and show how they can be properly quantified. Let us proceed as follows:
- We will solve the Schrödinger equation for a molecule (to any required degree of accuracy). This gives us functions (the canonical molecular orbitals) which tell us the electron density probability over the molecule as a whole.
- We now need to convert this (global) function to some sort of local property, since the concept of a bond is local, and not descriptive of the molecule as a whole. One such procedure is known as the NBO (Natural bond orbitals). A more formal description of this type of orbital is: Natural Bond Orbitals (NBOs) are localized few-center orbitals ("few" meaning typically 1 or 2, but occasionally more) that describe the Lewis-like molecular bonding pattern of electron pairs in optimally compact form. This can be precisely expressed in mathematical form (but we shall not do so here!); it is sufficient to say that the electron density probability predicted by summing all the occupied canonical molecular orbitals and alternatively all the local NBOs comes out the same! (i.e. there is more than one way of constructing a wavefunction for a molecule that predicts its overall electron density distribution, which in fact is the only properly measurable property).
- Just as with canonical MOs, where we had a (doubly) occupied set and a virtual (unoccupied) set, so the NBOs turn out to geometrically occupy the bonds (BD), the lower energy non-valence cores (CR), and the valence lone pairs (LP) of the molecule, with the unoccupied orbitals being represented by BD* and RY* (don't worry about this last one, it stands for Rydberg).
- In the NBO formalism, one can calculate an interaction energy between any doubly occupied BD or LP NBO, and any unoccupied BD* NBO. This can be represented in very simple terms by the diagram:
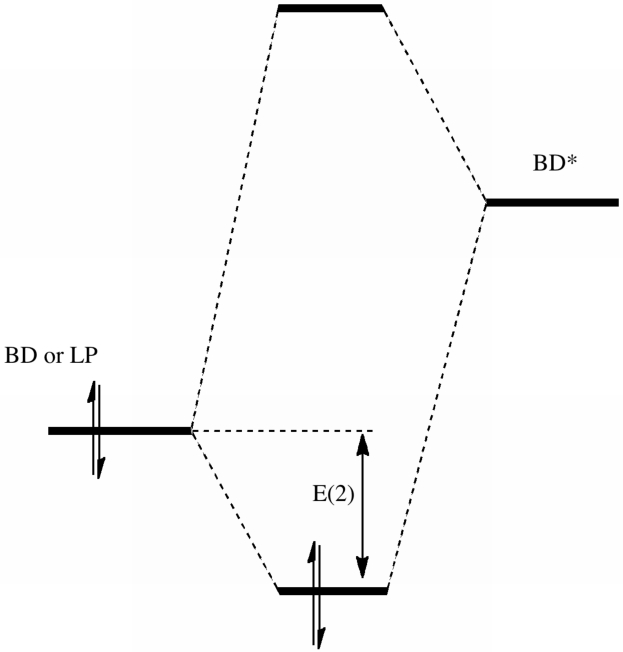
- This is exactly the form of the Klopman-Salem diagram you may well recollect from 2nd year conformational analysis lectures. But we have now made progress. By using the NBO expressions, we can obtain an exact value for the value of the quantity E(2).
- When this is done for the two dioxepins discussed in case study 1, the following results (at the B3LYP/6-31G(d) level) are obtained (with the keyword pop(nbo)) for the stable (green) and unstable (pink) forms;
- The only two large E(2) terms (both ~15.5 kcal/mol) are between an oxygen LP and a C-O BD* involving the adjacent oxygen. They correspond exactly to the two antiperiplanar interactions we first noticed by visualisation, but now we can precisely quantify these interactions.
- For the unstable isomer, only one large E(2) term is found (13.4); the other (7.5) is now significantly reduced because the orientation is no longer exactly antiperiplanar. The molecule is less stabilised and the two C-O bonds are no longer equal in length.
NBO analysis is very useful in a variety of situations, and is increasingly found in the literature. For example, it can be used to rationalise the gauche preference of 1,2-difluoroethane, and many others. Such E(2) NBO terms are thought to indicate useful chemistry down to energies of ~3 kcal/mol, and ones as high as 130 kcal/mol have been found (~15 is however typical of the anomeric effect). See this blog for another example where the unexpected was highlighted by such techniques.
I left this case study dangling, by posing the question: how was it determined that the helix is right handed? Watson and Crick actually answered this by stating (very briefly with no details) that a left handed helix could only be constructed by violating the permissible van der Waals contacts. The vdW contacts are actually very well modelled using molecular mechanics (the 4th term in the force field described here) and so a reasonable model could have been constructed using this technique to test this assertion. It suffers one slight deficiency. Because it uses force constants to define the terms, these are assumed to be the same everywhere throughout the molecule. Thus the rungs of the DNA ladder in the middle are treated the same as at the end of the helix. Is this justified? It is only very recently that vdW effects have been incorporated into quantum mechanical models in a manner which can be applied to large molecules (ωB97XD, see above). So we will kill two birds with one stone by jumping straight to this technique. We will also overcome another defect of mechanics, and that is the general lack of implementation for incorporating entropic effects on the energies. We will pose the new question: what are the relative free energies of and handed DNA helices (which, by the way are diastereomers, not enantiomers!). It turns out the answer depends on the nature of the base pairs.
- If they are exclusively C-G, as in d(CGCG)2, ΔG298 favours the left handed Z-helix by ~12 kcal/mol.
- If they are A-T, as in d(ATAT)2, the right handed B form is favoured by ~4.3 kcal/mol. As it happens, this is exactly what is known for small (tetramers) of DNA!
- Dispersion terms alone (van der Waals) make Z-d(CGCG)2 5.1 kcal/mol LESS stable than B-d(CGCG)2,
- Dispersion terms alone (van der Waals) make Z-d(ATAT)2 12.5 kcal/mol LESS stable than B-d(ATAT)2.
| System |
ΔΔG |
| ωB97XD/6-31G(d)/water. |
|
|
0.0 |
- Furanose oxygen within 2.85Å of a guanine ring
- Furanose OC-H hydrogen within 2.48Å of a second furanose oxygen
- Facilitated by C-Hσ/C-Oσ* anti-periplanar acidification (E2 5.8, magenta bonds)
- Anomeric interaction between iguanine and the ribose; NLp/C-Oσ*; E2 11.6 (violet bond).
- Cytosine-furanose anomeric (E2 6.8, indigo bond).
- Gauche-like conformation of the ethane-1,2-diol fragment (gold bond).
|
0.0 |
|
|
10.0 |
|
|
We conclude that Watson and Crick's model building, based on van der Waals analysis,
did indeed favour the B-DNA helical form, but that there are other aspects that can overcome this for
CG-rich DNA strands. See for example this blog for more details.
Bsck to scales|| Back to Visualisation| Back to Mechanics|On to Transition states| On to Advanced|
(c) H. S. Rzepa 1998-2012. No reproduction rights granted to this material without permission.


 We (think we) know where covalent σ-bonds are in molecules, they lie along the straight line connecting the nuclei of two atoms. We can idealize lone pairs on atoms such as oxygen, and in case study 1, all we needed was an (X-ray) structure to spot a connection between the (antiperiplanar) orientation of (certain) such idealized lone pairs and the C-O bonds in the molecule. But are the lone pairs really where we have idealized them? And in dealing the orientation of the lone pair with a σ-bond, we become aware that we are actually dealing with a concept derived from the Klopman-Salem equation, which uses not so much the two-electron σ-bond, as a vacant orbital occupying the (assumed) same orientation known as the σ*-bond. This was the basis of the
We (think we) know where covalent σ-bonds are in molecules, they lie along the straight line connecting the nuclei of two atoms. We can idealize lone pairs on atoms such as oxygen, and in case study 1, all we needed was an (X-ray) structure to spot a connection between the (antiperiplanar) orientation of (certain) such idealized lone pairs and the C-O bonds in the molecule. But are the lone pairs really where we have idealized them? And in dealing the orientation of the lone pair with a σ-bond, we become aware that we are actually dealing with a concept derived from the Klopman-Salem equation, which uses not so much the two-electron σ-bond, as a vacant orbital occupying the (assumed) same orientation known as the σ*-bond. This was the basis of the 