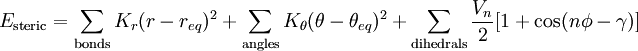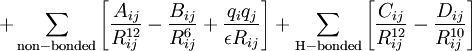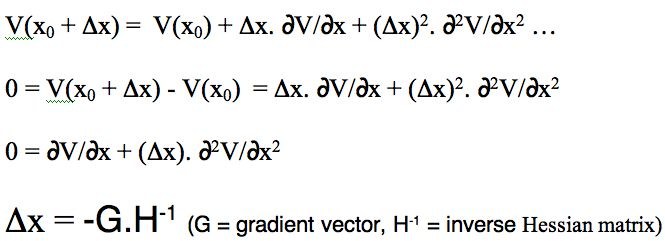Steric energy normalised relative to zero rather than any thermodynamic quantity.
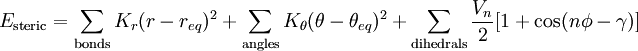
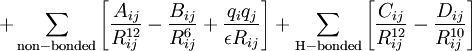
The parameters in the above equations require definition of
the atom types (hybridisation
of each atom; carbon has perhaps six different useful hybridisations) and an explicit definition of where one thinks the
bonds are and of what type (single, double,
delocalised etc). For bond lengths (1st term), each parameter
(force constant K) is specific to the particular
atom-type pair. A great many different atom-type pairwise combinations are
possible from the elements of the periodic table; few force
fields have even a fraction of these permutations.
A force constant K is also needed for each three-atom bend combination.
For the torsional 3rd term, parameters are inserted only for the common single and double bonds.
ψ is the dihedral angle
γ is a phase factor depending on whether ψ=0 is a minimum or maximum
n is a` symmetry number
The fourth term relates to non-bonded interactions (it implies we know where there are no bonds!). It requires knowledge of
The second part of this term accounts for the dispersion energy.
The electrostatic last part of this term requires charges on each atom pair (approximated with various relatively crude charge schemes, often obtained from quantum mechanical calculations on tiny molecules representing typical functional groups)
Many (often proprietary) force fields include a fifth additional term in the sum above, relating to:
hydrogen bonding, or
π-conjugation, or
anomeric effects, etc
There are also a rather simpler so-called universal or full periodic table force field (UFF, DOI: 10.1021/ja00051a040) where an attempt is made to interpolate atom pair or atom triple values from the basic hybridization specified for each atom, and specific values for each atom. These are not very good for energies, but suffice for cleaning up a crudely drawn structure. They can also be applied to many more elements of the periodic table than the MM2/3/4 style force fields.
Some mechanics implementations insert cross-terms, ie stretch-bend. This implies that say a bond far from its equilibrium length may bend differently from one of normal length. One could also envisage a need for e.g changing the atom charges on say a polar carbonyl group as a function of its stretched bond length (this is never in practice done). There are an enormous number of potential cross terms, the vast majority of which are in fact neglected. For large molecules (say DNA) this may in fact be a significant error.
As an approximate rule of thumb, the first three terms in the above equation tend to zero for unstrained and unhindered molecules. A high positive value of the steric energy is therefore taken as an indication of instability. The fourth term can take on negative values, particularly if the molecule is globular (lots of non-bonded attractive terms) or if the molecule has many ionic interactions where qi and qj have opposite signs.
Force field parameters can be of widely differing quality. Some are derived from accurate experimental measurements, others may be pure guesses, or interpolations. Some force fields are good for energies, others for geometries.
A good summary of the more widely used force fields can be found here.
Energies should only ever be compared for isomers with the same total number of atom/bond types, in other words using the same parameters.
Energies should not be compared across different force fields, across different programs implementing ostensibly the same force field, or even across different versions of the same program!
2. Using MM to optimise a molecular geometry
The steric energy is used in conjunction with a "geometry optimiser" to find local minima in the energy. The process starts with a Taylor series expansion of the potential energy as a function of a the coordinates (show in the diagram below for just one coordinate, but generalized later to 3N-6). The expansion is truncated to correspond to a harmonic or quadratic potential surface:
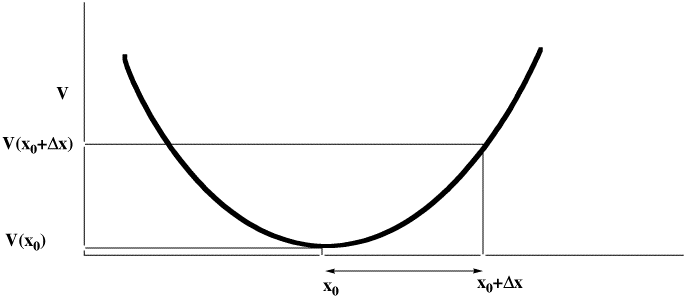
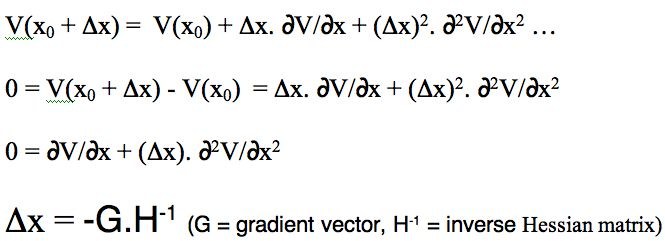
There are four ways of populating the inverse Hessian matrix:
steepest descent, which sets the diagonal terms to 1, and all the others to zero. Very fast, particularly initially, and suitable for the largest molecules since no matrix inversion need be performed.
conjugate gradient, which evaluates the value of only the diagonal terms, setting all the others to zero. Slower, but meanders less when the gradient is no longer "steep".
BFGS, which evaluates the diagonal terms, and approximates the off-diagonal terms from the history of the optimisation. Much slower, and less suitable for large molecules, since inverting the Hessian is now increasingly time consuming.
Newton-Raphson, which evaluates all the terms. Extremely slow, but can succeed when all other methods fail (opt(calcall) keyword in Gaussian!).
The value of Δx is obtained from a one-dimensional line search to obtain a scaling factor (normally around 0.25), and an iterative process started. Convergence is achieved when either the value of Δx reaches a small predetermined value, or the change in energy between successive cycles becomes small.
3. Summary of Pros and Cons of Molecular Mechanics
Pros:
Simple energy functions are quick to solve,
can cope with large molecules,
accurate for systems which are close to the models used to reproduce the force field (interpolative),
The minima found are restricted to the "atom-connectivity" specified in the input file; no bonds can make/break during the optimisation process (and hence no matter how bad the initial geometry guess is, that connectivity will be preserved). Hence very useful for instantly converting sketches of molecules into tidied coordinates, even in an on-the-fly manner (elastic band optimisers)
deals reasonably accurately with van der Waals interactions at non-bonded distances for larger molecules (which increase vastly in number as the molecule gets bigger and which are notoriously difficult to model using purely quantum mechanics)
Mechanics, when used with high quality parameter sets, can be very reliable for calculating vibrational properties (IR frequencies, but not intensities which are an electronic property). See also the cons
Mechanics is good for conformational exploration (Monte-Carlo, Genetic algorithms, etc) where the number of possible conformations can number millions. It is used in this context for NMR predictions of molecules where many possible conformations may exist.
Mechanics is highly applicable to molecular dynamics, and hence derived statistical thermodynamic quantities such as free energies etc. In this context it is frequently used for analysing proteins, and other large biomolecules.
Cons:
No unique functional form for the energy terms (= proprietary?)
Number of parameters rises rapidly for non-CHNO elements,
Need to know atom/bond type for all the molecule (non-classical bonding)
Does not include majority of cross terms in force field
Most mechanics implementations do not compute 2nd derivatives (entropy)
Cannot cope with unusual (= unpredicted) bonding or interactions
Mechanics is prone to "false minima", allowed by the equations,
but physically unrealistic (e.g. hemispherical carbon)
Cannot be used for bond-breaking transition states and hence reactions.
Organic chemists are taught that carbonium ion stability is predominantly due to electronic factors such as whether they are primary, secondary, tertiary, allylic, benzylic etc. What is mentioned much less is that their relative stability is also very sensitive to their geometries, and in particular the angles of the three substituents at the carbon. Geometries of carbonium ions are particularly inaccessible; it is not easy at all to get crystal structures! So how can Molecular Mechanics model the following carbonium ions? They are arranged in the expected order of increasing stability. Notice that the MM2 method gradually decreases the predicted angle energies. Notice also however how it predicts that the tertiary carbonium ion is actually LESS stable than the preceeding primary ion, which is surprising to say the least. Clearly, electronic factors must be playing an important role as well. Suffice to say that even without ANY consideration of electronic factors, the MM2 method does not do too badly in its prediction of relative stabilities. This re-enforces the conclusion that bond angles in carbonium ions are just as important as substitution! See also DOI: 10.1021/ed800058c for more detail.
stretch = 0.868 angle = 19.173
stretch bend = -0.672 dihedral = 6.497
improp torsion= 0.155 van der Waals = 2.663
electrostatics= -1.341 hydrogen bond = 0.000
Energy of the final structure is 27.342 kcal/mol.
(QM B3LYP/cc-pVTZ → rearranges to final
product directly by breaking/forming bonds)
stretch = 0.447 angle = 18.758
stretch bend = -0.078 dihedral = 6.916
improp torsion= 1.124 van der Waals = 1.622
electrostatics= 0.000 hydrogen bond = 0.000
Energy of the final structure is 28.788 kcal/mol.
(Relative QM B3LYP/cc-pVTZ free energy
= 25.7 Kcal/mol)
stretch = 0.571 angle = 5.694
stretch bend = -0.027 dihedral = 7.179
improp torsion= 0.009 van der Waals = 5.678
electrostatics= -0.545 hydrogen bond = 0.000
Energy of the final structure is 18.559 kcal/mol.
(Relative QM B3LYP/cc-pVTZ free energy
= 23.3 Kcal/mol)
stretch = 0.512 angle = 3.439
stretch bend = -0.153 dihedral = 6.662
improp torsion= 0.002 van der Waals = 3.872
electrostatics= 0.683 hydrogen bond = 0.000
Energy of the final structure is 15.017 kcal/mol.
(Relative QM B3LYP/cc-pVTZ free energy
= 0 Kcal/mol)
The H-bond energy functions in the Mechanics method are normally specifically parameterised against standard models, which involve three atoms, ie X...H...Y. The model of hydrogen bonding in this molecule is unusual to say the least, since it involves a whole ring and not a single atom as the H acceptor, and hence the Mechanics method (in theory) has no functional form which can reproduce it. In particular, aromatic rings are attractive to electrophiles by virtue of their quadrupole moment, which is a higher order property of the charge distribution (thus the so-called multipole expansion goes as monopole charge, dipole, quadrupole, octapole and hexadecapole. The equations above in effect only include the first and possibly second term of this expansion).
The optimised geometry does predict what looks like H-bonding, but its directionality is not quite correct. The steric energy is -49 compared with -18 if the two components are infinitely separated. This makes the binding energy = -31 kcal/mol. In this case, it is predicted to arise almost entirely from the non-bonded van der Waals term rather than electrostatic or hydrogen bonding (dipole-dipole) terms.
There is one final aspect which must be considered, namely the entropy of the interaction. The equation
ΔG = ΔH - T.ΔS
implies that if entropy decreases (i.e. ΔS is -ve) as a result of a reaction (or in this case a binding, in which two free molecules are reduced to one bound complex), then ΔG must increase (two -ve signs = a positive result) as a result by the amount T.ΔS. The Mechanics method could in principle provide an estimate of this term via calculation of the normal modes of vibration (and solution of the appropriate partition function equations), but few Mechanics programs actually perform this calculation (which requires the second derivatives to be evaluated, something only available using MM4, accurate to between 25-50 cm-1). An approximate estimate of T.ΔS is about -(12-15) kcal/mol at 298K (i.e. approx 2 kcal/mol per degree of lost freedom), which has to be added (-/- = +) to the binding energy obtained above, to obtain a final value of -(15) kcal/mol. This value is certainly in the correct ballpark.
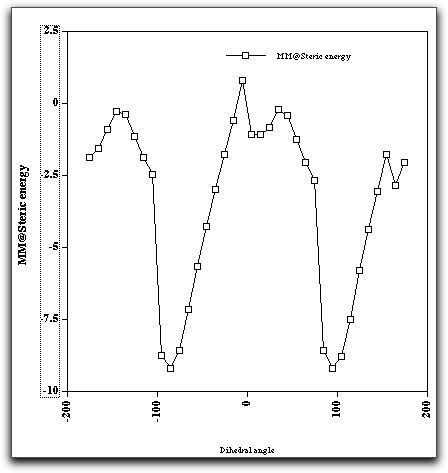
Another property of this molecule can also be studied using molecular mechanics, namely the rotation and preferred orientation of the aryl-C bond, for which mechanics is very well suited. The following "dihedral driving" calculation shows the MM2 energy as a function of the dihedral angle between the trifluoromethyl group and the anthracene ring. The barrier (about 10-11 kcal/mol) compares reasonably well with the measured value of ΔG (from NMR lineshape analysis) of about 14 kcal/mol. The discrepancy may well be due to ignoring solvation of the OH group, which increases its size, and hence the barrier.
Reference: M. L. Webb and H. S. Rzepa, Chirality, 1994, 6, 245-250. DOI: 10.1002/chir.530060406
Now that we have a quantitative method for estimating energies of molecules, we can tackle a problem such as shown below. An application of "shape design" is the recent area of designing catalysts to promote reactions by ensnaring them in a cavity, or binding pocket. Whilst designing enzymes to do this is somewhat beyond the scope of the current course, a simple example of small molecule design can be shown here. A resorcinol-anthracene based aromatic molecule was designed in the form of spacers (the aromatic rings) and links (in the form of hydrogen-bonds) to create in the solid state a system with well defined cavities, which are large enough to accommodate small organic molecules, such as ethyl methacrylate and cyclohexadiene. The former is held within the cage by further hydrogen bonds to the cavity lattice. In particular, various changes to the structure can be made, to increase or decrease steric bulk, etc and the effects of these changes can be modelled, ie predicted.
The previous systems were modelled by drawing/creating the model using the built-in editor (ChemBio3D, etc). Here we will be importing the X-ray derived coordinates. There are some important considerations to doing so.
Applying the Mechanics model requires explicit assignment of force constants for ALL atom types, which in turn requires the hybridisation (sp, sp2, sp3) of all centres to be fully known. No intermediate hybridisations are allowed.
Conversion from X-ray coordinates to a format where all atom and bond types are fully defined (e.g. the MDL Molfile) is not 100% reliable. In particular, the hybridisation must be deduced from a combination of the bond lengths of all substituents at a given atom, the total coordination, and probably the angles (ie sp2 assumes the central atom is coplanar with three surrounding atoms).
The Molfile we are loading here was very carefully edited by hand to ensure that:
the aromatic rings all had correct atom types, to allow aromaticity to be detected
the small organic molecules trapped in the cavity were actually "disordered" in the X-ray structure. This means that even the H count on any given carbon atom has to be carefully checked.
In this example, all H-bonds were in fact "conventional" and hence the H-bond term in the Mechanics force field can be automatically applied.
We will see in the Quantum Mechanics section how all these limitations can be removed.
When a standard MM2 mechanics force field is applied to the resorcinol-anthracene anvil, the following results are obtained:
Component
MM2, kcal/mol
Supermolecule
-157.2
Supermolecule without substrates (Anvil)
-140.1
Anvil computed as four components
-92.8
Three Substrates together, without anvil
+14.2
Three separated Substrates
+23.4
Anvil + Substrates separately
-140.1+14.2=-125.9
Binding Energy of substrates to anvil
-157.2-(-125.9)=-31.3
These energies are NOT corrected for entropy (i.e. they are closer (but not quite) enthalpic, and not free energies) a significant limitation. Very likely this sort of catalyst functions by converting enthalpic energies (the binding of the catalyst components) into entropic energies (i.e. pre-organising the reactants in the cavity, which of course consumes entropy. The free energy cost of assembling the three substrates is likely to be around +24-30 kcal/mol, but this is still likely to result in a win!).
What IS useful with the mechanics approach is the ability now to make minor variations to the environment, such as changing the nature of the substrates included in the centre of the anvil to see how the binding energy responds. Its a tuning procedure!
Literature Citation. Catalysis by Organic Solids. Stereoselective Diels-Alder Reactions Promoted by Microporous Molecular Crystals Having an Extensive Hydrogen-Bonded Network, K. Endo, T. Koike, T. Sawaki, O. Hayashida, H. Masuda, and Y. Aoyama, J. Am. Chem. Soc., 1997, 4117 - 4122; DOI: 10.1021/ja964198s
An interesting alternative to the above anvil is the molecular "tennis ball" (e.g. DOI) elaborated by Julius Rebek. Quite large molecules can be enclosed in these balls, and once in, they organize themselves very specifically, a phenomenon Rebek has termed molecular "social isomerism" (DOI: 10.1002/anie.200462839)
Just as with the anvil, the tennis ball is held together with hydrogen bonds, and this can be modelled using the Mechanics method, as can the organisation of the ligands inside the cavity.
Here, the energy liberated upon dimerisation is 62 kcal/mol, of which 41 is due to the non-bonded dispersion terms and 21 to hydrogen bonds. This is more than enough to overcome the entropic terms which acrue when substrates are trapped inside.
