Techniques of Molecular Modelling: Stereochemistry
A key stage in the reaction sequence shown as part of the problem is the following step involving C-C bond formation to an aldehyde, mediated by the chiral auxilliary X=di-isopinocampheyl (see DOI: 10.1016/S0040-4020(01)85588-5 and 10.1016/S0040-4020(01)86409-7)
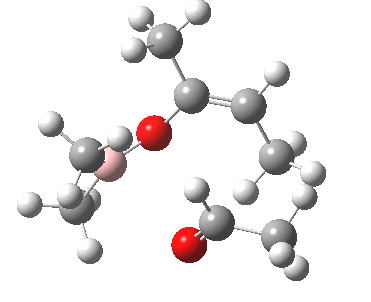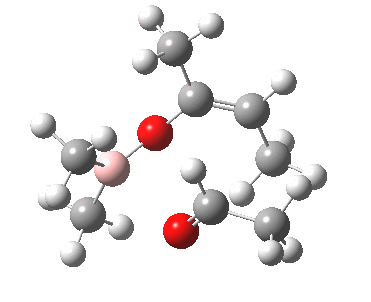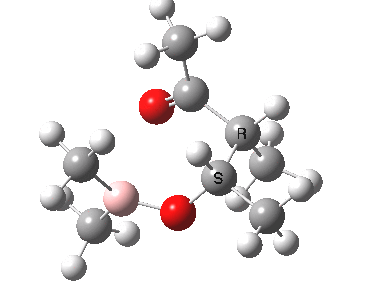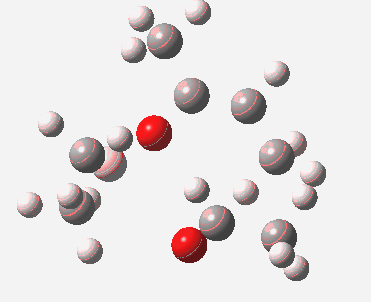
Other than the chiral auxiliary, all the reagent components are achiral.
However, two entirely new chiral centres are formed in the product.
Modelling can help us understand two features of these new chiral centres
and why they form so specifically.
- their relative stereochemistry: R,R vs R,S (and their enantiomers S,S vs S,R in the absence of any other chiral centre)
- their absolute stereochemistry: R,R vs R,S vs S,S vs S,R in the presence of another chiral centre X
The Relative Stereochemistry
A 3D model for the basic framework (i.e. replacing all substituents with H) of the transition state must be constructed. Since this involves bond formation and cleavage, a QM (Quantum Mechanics) based model must be used, in this case the AM1 semi-empirical method (Table). The transition state can be located using a variety of methods. Since the reaction involves two bonds making and one breaking, its difficult to construct a 1D or 2D grid. The easiest way is to guess the approximate lengths of the breaking/making bonds (about 1.9 - 2.1A), and optimise the geometry with these values constrained (using eg the opt(modredundant) keyword in Gaussian). The resulting geometry can then be fully optimised with no such constraints, but this time with the use of appropriate transition state location algorithm such as the eigenvector following method and specifying a transition state to be found (opt(calcfc,ts)).
These calculations ( ) reveal that both and of the transition state are possible. A full calculation of the 2nd derivative matrix, followed by appropriate mass weighting, will give the frequencies of the various normal modes of the molecule. One is shown as -ve (imaginary), being the transition state normal mode. A program such as JMol can be used to animate the form of this normal mode.
One next needs to understand how the various substitution sites interact sterically.
To do this, methyl groups are inserted into the various positions
(including one for the chiral auxilliary X) and the energies of some
of the various possible isomers are calculated.
The is again the most stable. is formed with the thus avoiding steric congestion from the . This particular steric interaction in effect defines which π face of the carbonyl group is used to form the new C-C bond. Forming the C-C bond from the alternative face of the carbonyl would place the This interacts sterically with the chiral auxilliary and is 3 kcal/mol higher in energy, and hence not formed. Another way of avoiding steric congestion is for the to form. The methyl adopts an equatorial position, but it is eclipsed rather than staggered with the and hence the most stable boat isomer is 3 kcal/mol higher than the chair.
|
|
|
|
|
|
|
|
|
|
| 0.0 | 3.0 | 0.0 | 4.7 | 2.8 | 1.5 | 0.0 | 2.9 | 0.0 |
|
|
|
The Absolute Stereochemistry
The methyl group X must now be replaced with a chiral auxilliary. Many such auxiliaries can be used (most derived from natural products that are enantiomerically pure). To start with a simple model, will use the (un-natural) group -CHClI which contains three ligands of quite different size. Its chirality is defined in these models as S. When inserted into the model, two diastereoisomers with carbon chirality of or can be formed. The calculations reveal that one of these is about 1.5 kcal/mol more stable than the other, which is the correct order of magnitude to result in chiral induction. A more "natural" chiral group derived from camphor can now be inserted to form the final models and in this instance a rather larger energy difference is obtained. Using this last value in the equation ΔΔG = -RT Ln [R,S]/[S,R], we get [R,S]/[S,R] = ~130, an enantiomeric excess of better than 99%.
The Strecker synthesis represents a rapid way of constructing amino acids of specified configuration (see case study 3). The reaction comes in two parts. The first involves building a sulfoxide-based (S)-chiral auxilliary to an imine. The second part of the reaction involves nucleophilic attack on this imine with an aluminium cyanide reagent to form an (S,S) diastereoisome, via a postulated cyclic six-membered ring transition state, and subsquent hydrolysis of the cyano group to an enantiopure amino acid. Can this mechanism be verified using molecular modelling?
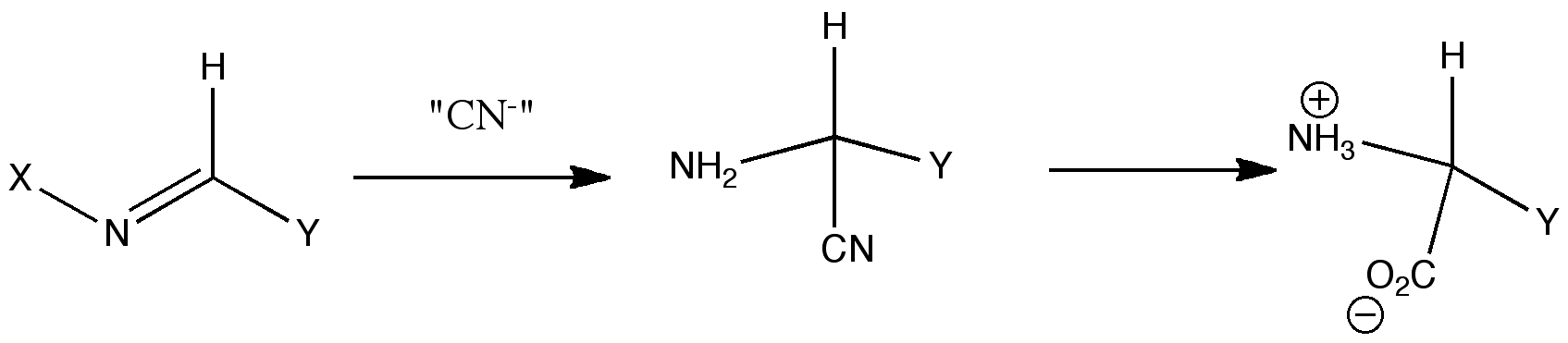
| A: Is the currently acepted mechanisms for the Strecker reaction a good model? |
| System |
Relative free energy |
digital Repository |
|
The carried out by Franklin Davis involves the following precursors, the N-(Phenylsulfonyl) (3,3-dichlorocamphoryl) oxaziridine (derived from a natural product in pure enantiomeric form, 10.1021/ja00030a045), from which an oxygen atom is delivered to produce enantiomerically pure sulfoxide. The transition states for the diastereomeric transition states are controlled by the 3,3-dichloro functionality, preventing rotation about the O...S bond. The a N=CH...O hydrogen bond in the (SS) isomer is at least in part responsible for diastereoselection (cf HUGHAS)
|
|
|
4.5 |
10042/to-144 |
|
|
0.0 |
10042/to-145 |
|
The Davis mechanism for the Strecker proper now involves the aluminium reagent forming an , which reacts with the sulfoxide to form which undergoes asymmetric transfer of cyanide via TS1, a six-membered ring transition state.
|
| There is only one snag: no actual such transition state can be located at the B3LYP/cc-pVTZ level! |
|
|
| B: A modified mechanism. Will it be any better? |
| System |
Relative free energy |
digital Repository |
|
The story is now taken over by Pedro Merino (10.1016/S0957-4166(02)00832-7), where we see the suggestion that the chair six-membered ring assumed by Davis et al (TS1)
cannot exist unless an additional molecule of water/solvent is involved, as in . Had transfer of CN occured as Davis described, the Aluminum would have ended up with an empty coordination site, and this is now prevented by intermolecular SN2 like displacement by water/solvent.
|
| The problem with this mechanism is that a bimolecular mechanism incurs an entropy penalty, which as we have seen before adds about 10-12 kcal/mol to the ΔG for the reaction! This contributes to the calculated barrier of 36 kcal/mol, which is too high to be a facile reaction at room temperature. |
|
This mechanism too is broken. Back to first principles. Davis assumed that the active reagent is monomeric R2Al-CN, which is formed by opening a presumed aluminium dimer. Checking the crystal structures of related compounds suggests instead a (e.g. 3) where both the N AND the C of the cyano group can coordinate to the Al; dissociation of this trimer could lead to either an Al-CN or an Al-NC species.
|
|
|
| C: A new, improved mechanism that fits the facts! |
|
Coordination to 1 can now give essentially isoenergetic or complex with the chiral imine-sulfoxide.
|
|
This leads to a new model, , which involves a 7-membered ring in which an iso-cyano group also plays the role of the solvent in TS1, and the resulting unimolecular nature saves the entropy term that was needed for TS1a.
|
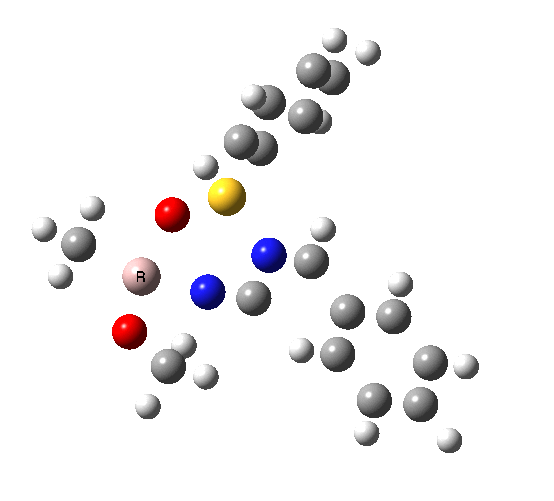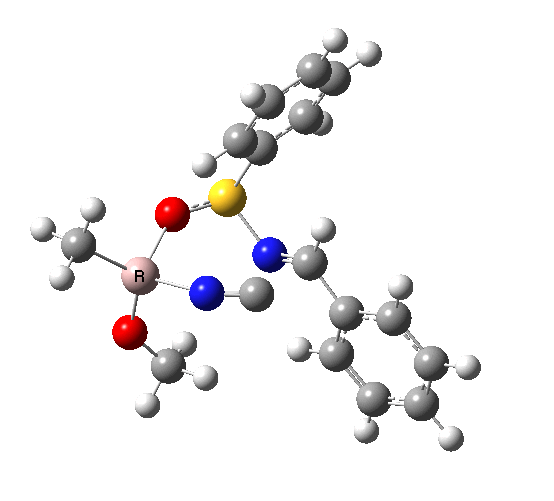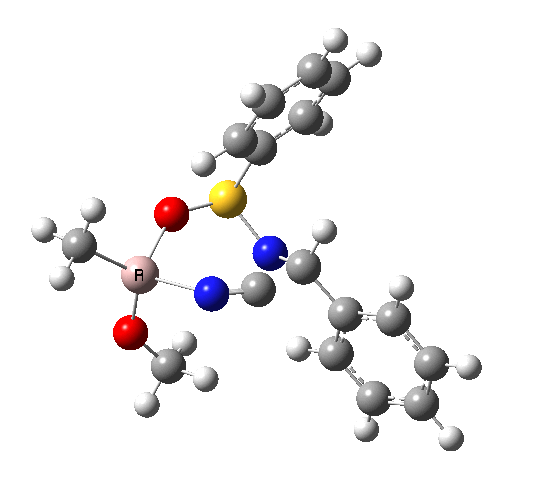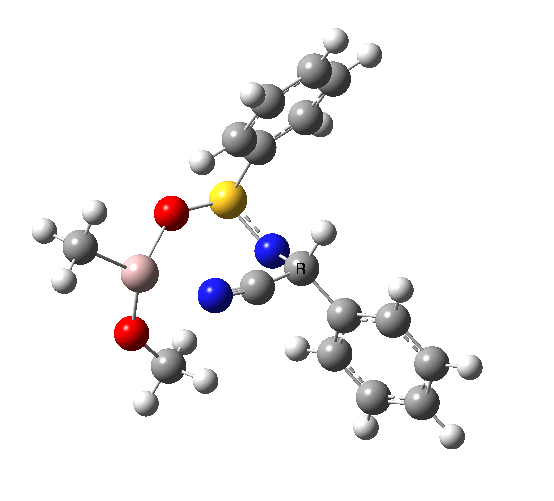 |
|
|
23.9 |
10042/to-120 |
|
|
22.2 |
10042/to-122 |
| TS2 has a more favourable Dunitz angle (104° vs 112° for TS1a). The product 4 can be fully decomposed by treatment with water, via transition state TS4. The barrier for this reaction, although requiring the now notorious 10 kcal/mol of entropic contribution, is nevertheless lower than TS2. Because the entropic step comes much later in the mechanism, it is no longer relevant!. |
|
The form of TS2 is 1.7 kcal/mol higher (B3LYP/cc-pVTZ) than the form, due predominantly to the former being disfavoured due to the between a hydrogen and the phenyl group. In stark contrast, using TS1a as one's model, the (S,R) diastereoisomer is instead 0.8 kcal/mol lower than the (S,S).
|
|
|
| D: Tidying up the loose ends |
|
The calculations show that TS2 is favoured over by about 17 kcal/mol, as is the product 4 over product 5.
|
| The effect of replacing an alkyl group on the Al catalyst with an ethoxy or methoxy group has the effect of increasing the barrier to the reaction, and hence slowing it down (making it more selective). With the model TS1a, such substitution is predicted to have the opposite effect, decreasing the barrier by 2.7 kcal/mol. With model TS2, the barrier is predicted to increase by 1.9 kcal/mol, thus accounting for the selectivity. |
QED. THE END
By special request, the following is added to give an example of study
of polymerisation mechanisms. It is not examinable.
The Ti-based Alkene Polymerisation systems
The (isotactic) polymerisation of alkenes such as propene constitutes a very important industrial process. This is accomplished on an
industrial scale using the Ziegler-Natta catalyst, which comprises a solid support of MgCl2 doped on the surface with TiCl4 which
is then treated with a methylating agent such as Me3Al. It is thought that one Cl on the Ti is replaced with Me to form the active catalyst. This system when treated with
e.g. propene then produces stereoregular polypropylene. This has the
remarkable property of forming a helix, similar indeed to DNA, due to the regular configuration at the carbon atoms marked as orange in the model below. You could try
building your own polymer here!
Clearly, the shape and electronic nature of the transition stage for this reaction need to be characterised, and from this the steric environment understood.
|
Firstly, the MgCl2 needs to be modelled. This is normally done using a mathematical method known as the periodic boundary solution, where a small section of the latice is
repeated in all three dimensions to produce an approximate solution for an infinite lattice. Modern so-called density functional methods using plane waves are particularly suitable for this solution.
The selected surface of this lattice then is doped with a molecule of TiCl3Me, and geometry of this molecule recalculated to allow for the effects of interaction with the lattice and also any relaxation within the lattice. In reality, the changes are actually fairly small, and we will ignore them in the present analysis.
|
|
|
To the now isolated model Cl3TiMe system, an ethene is
occupying one of the three equatorial positions surrounding the trigonal bipyramidal Ti atom. Notice its orientation at this stage.
A insertion reaction takes place, akin to a 2+2 cycloaddition reaction. Notice how the ethene has to rotate by 90 degrees in order for the
C-C bond to form. Also notice the α-agostic interaction formed in the transition state. The has a β-agostic interaction, which helps to orient the extruding polymer chain in a direction which keeps a coordination site on the Ti open and hence is still receptive to coordination
by the next alkene. Overall,the carbon ligand on the Ti is now converted from Me to Pr, i.e. 2 carbon atoms have been added. Even now, the geometry of the Ti-propyl product
is mediated by a strong β agostic interaction between the Ti atom and the H-C bond from the methylene group now joined to the Now the process can repeat, and with each step, the polymer chain would increase by two atoms.
|
|
|
The final stage in the modelling is to substitute propene instead of ethene as the alkene. The additional can occupy one of four different locations. These the MgCl2 lattice. This one by the now itself held rigid by an α-agostic transition state interaction (it changes to β in the product) leaving only . Each successive propene will now be added in which the Me group has the same geometrical relationship to the
polymer chain as all the preceeding steps. In effect, stereoregular polymerisation has been achieved.
The ability to model all the stages in such a subtle mechanism allows changes to the catalyst, the surface, the ligands etc to be investigated, and in this manner to allow facile design of potentially new and improved catalysts.
|
.
|
For further details on the Ti system see J. Gale, R. Catlow, M. Gillen, Topics in Catalysis, 1999, 9, 235-250. DOI: 10.1023/A:1019174908887
back to scales|| Back to Visualisation|Back to Mechanics|Back to MO Reactants| Back to MO Transition states|
This course is no longer being presented, and the materials here should be regarded as historical
(c) H. S. Rzepa 1998-2012. No reproduction rights granted to this material without permission.



