Way back in 1977, the crystal structure of the sulfur ring S7 was reported.[cite]10.1002/anie.197707151[/cite] The authors noted that “The δ modification of S7 contains bonds of widely differing length: this has never been observed before in an unsubstituted molecule.” No explanation was offered, although they note that similar effects have been observed in S8O, S7I+ and S7O. The S7 molecule was yesterday brought to my attention (thanks Derek!) over a pub lunch and in the time honoured manner of scientists, sketched out on a napkin – with a pen obtained from the waitress!. As an “organic chemist”, I immediately thought “anomeric effects”. And so indeed it has proven. A calculation using the MN15L/Def2-TZVPP DFT method and analysis using the Weinhold NBO7 procedure[cite]10.14469/hpc/15228[/cite] reveals the following structure (with Cs symmetry) and indeed the four unique S-S distances are all different (experimental values in parentheses). So how does this arise?
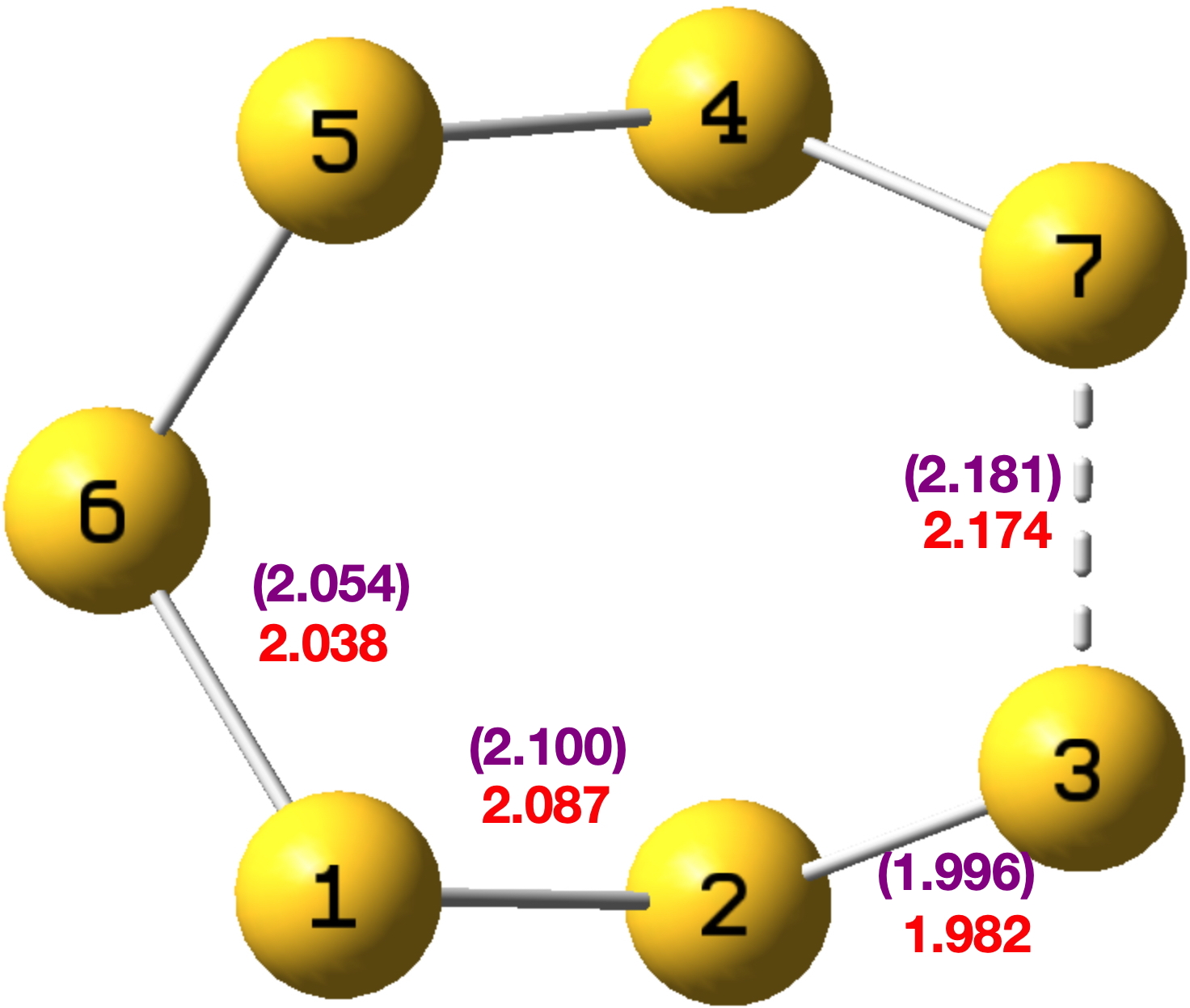
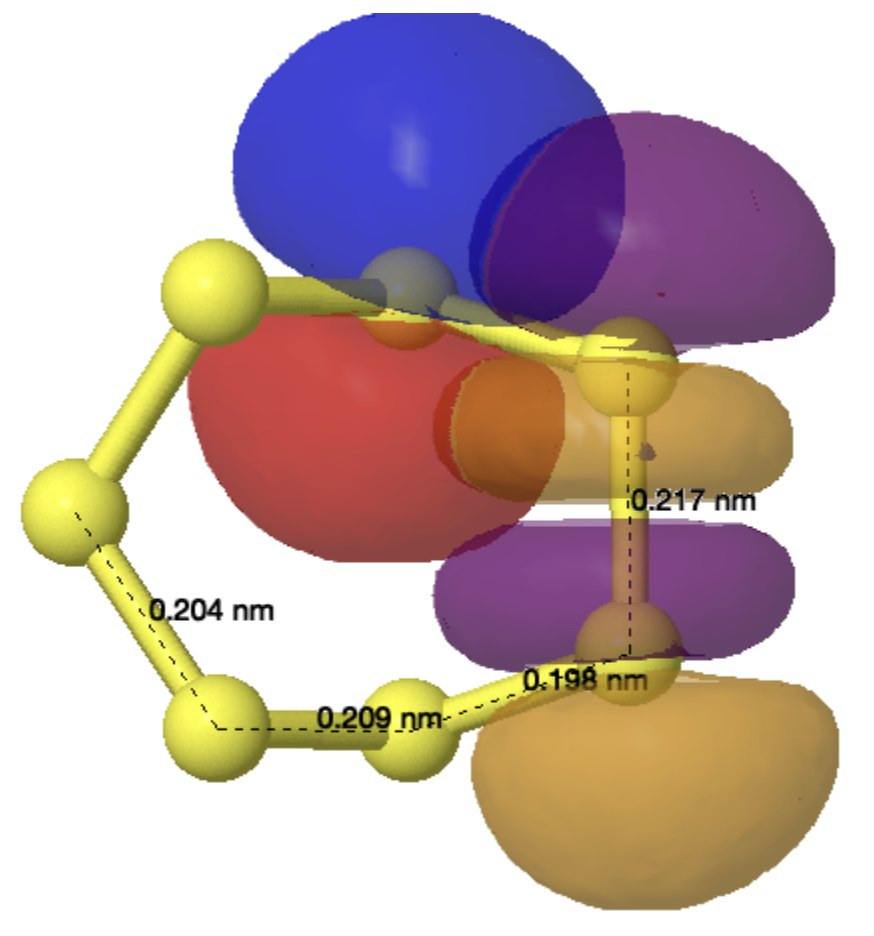
Effect 1 is the donation of a lone pair from sulfur S4 or S2 into the antibonding orbital of the long S3-S7 bond labelled 2.174Å. The NBO E(2) perturbation energy is 12.35 kcal/mol, a fairly large effect when you consider that the more conventional value involving oxygen instead of sulfur is ~16 kcal/mol. There are two such donations (black and red) and so this long bond is doubly lengthened. Simultaneously the S4-S7 or S2-S3 bonds associated with the donor sulfur are shortened to 1.982Å.
You can see the orbitals involved below (click on the image to obtain a 3D rotatable model) and consider that the blue phase overlaps positively with the purple and also the red with orange. These overlaps conspire to move electrons from the S4 lone pair into the S4-S7 bond and to move electrons from the S3-S7 bond into an S3 lone pair and hence to shorten the first to give it some π-bond character (Wiberg bond index 1.1796) and to lengthen the second bond (Wiberg bond index 0.8295).
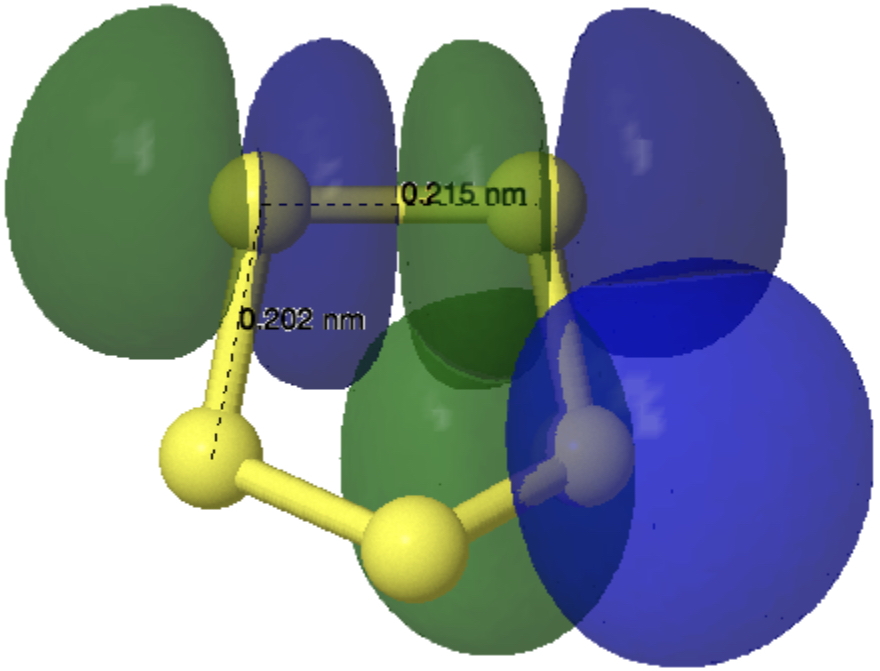
Effect 2 is the donation of a lone pair from sulfur S3 or S7 into the antibonding orbital of the S1-S2 bond with length 2.087Å. Only one donation – E(2) is now 10.12 kcal/mol – for each of the two S-S antibonding orbitals occurs (S1-S2 and S4-S5) and hence the lengthening of these is less than before. This again serves to shorten the S2-S3 and S4-S7 bonds labelled with the distance of 1.982Å
A smaller effect (E(2) 4.6 kcal/mol) occurs between S2/S4 and S1-S6/S5-S6.
So this adds a nice stereoelectronic explanation to an observation made almost 50 years ago. Perhaps this example should be included in all taught inorganic curricula?
Postscript: The S-S stretching frequencies vary a great deal. The symmetric and antisymmetric S2-S3 and S4-S7 modes are respectively ν 564 and 557 cm-1 whilst the S3-S7 mode is way less at 370 cm-1
Postscript 1: The smaller S5 ring also shows this effect, but to a smaller extent (E(2) = 6.1 kcal/mol) and νS1-S2 = 382 vs 546 and 540cm-1
Also for fun, how about singlet state cyclo-O7 (heptaoxolane)? Unsurprisingly, the anomeric effects noted for S7 itself are amplified to the point that the molecule dissociates to O3 and 2O2 (singlet).
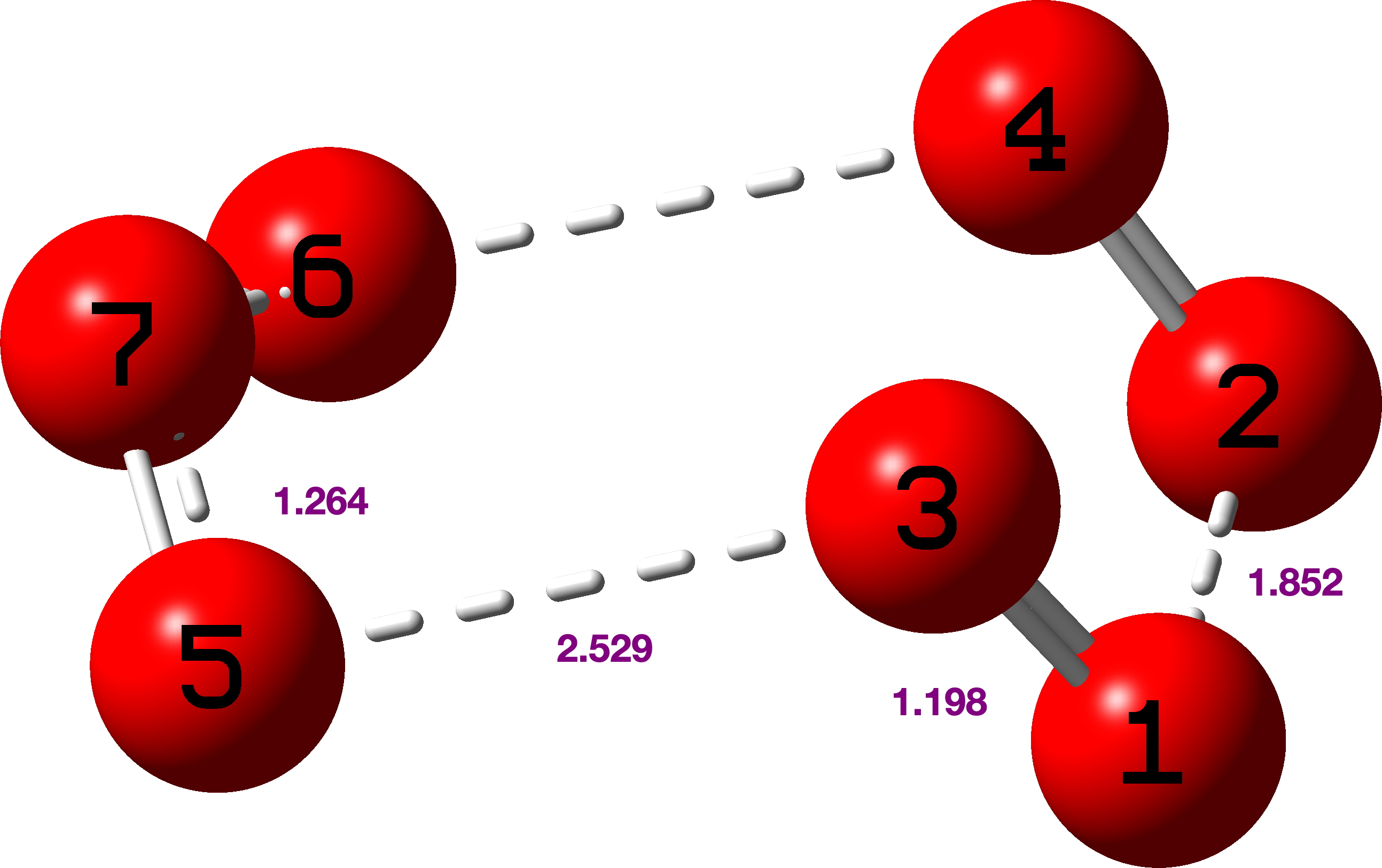
Finally, singlet state cyclo-O5 (pentaoxolane)
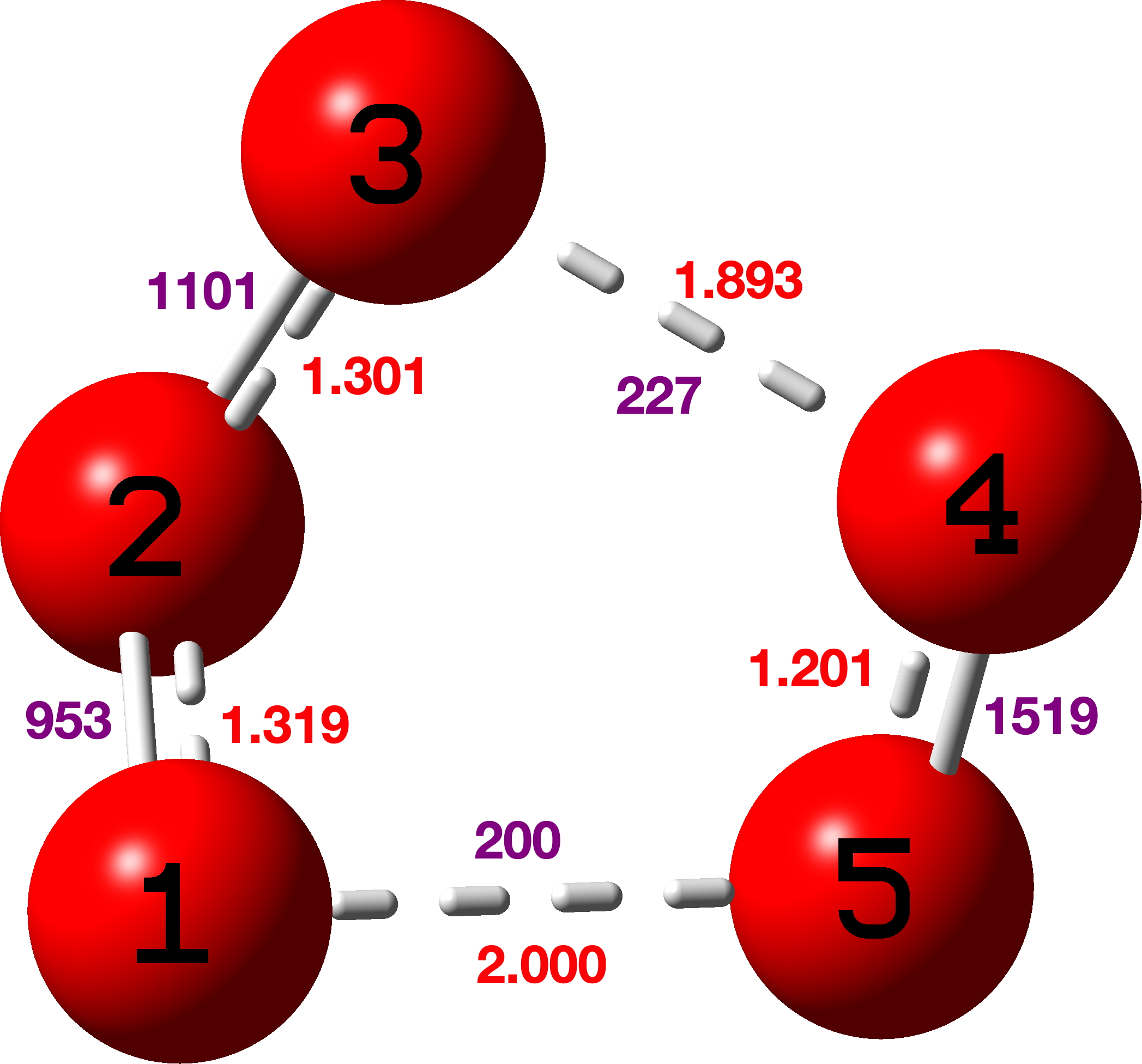
Here νO-O cover the remarkable range from 1519, 1101, 953, 227 to 200 cm-1 (purple values in diagram above)
These vibrations are associated with the following NBO E(2) Energies; O2Lp-O3O4σ* 34.1, O2Lp-O1O5σ* 23.3, O4Lp-O1O5σ* 20.7, O5Lp-O3O4σ* 19.9, O1Lp-O2O3σ* 12.1, O3Lp-O1O2σ* 10.6.
In addition to these lone pair to σ* interactions, there are two very high σ to σ* interactions (O1O5 to O3O4* 39.9 and O3O4 to O1O5* 33.5 kcal/mol) which strongly suggest very high so-called multi-reference character to the wavefunction.
Although not a molecule that is ever likely to be isolated in a laboratory, cyclo-O5 still has a lot to teach us.
