| Tabular Pericyclic Reaction Selection Rules | ||||
|---|---|---|---|---|
| Condition | + Electron count | + Stereochemistry ⇒ | Topology | ≡ Lk |
| 1: Heat (Δ) | 4n+2 | Suprafacial‡ | Hückel | 0† |
| 2: Light (hν) | 4n | Suprafacial‡ | Hückel | 0† |
| 3: Heat (Δ) | 4n | Odd antarafacial | Möbius | Odd |
| 4: Light (hν) | 4n+2 | Odd antarafacial | Möbius | Odd |
| Diagrammatic Pericyclic Reaction Selection Rules | ||||
| Frost, Musulin and Zimmermann diagram (1965) | ||||
‡Or even antarafacial †Or even Lk
Dewar and Zimmerman independently noticed that the symmetry properties of the molecular orbital correlation diagrams for pericyclic reactions are very similar to those obtained using eg Hückel theory for aromatic molecules. For example, the MO diagram for the electrocyclic conversion of hexatriene to cyclohexadiene is remarkably similar at its transition state to the ground state MOs of benzene;
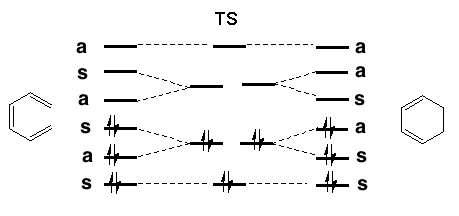
The rules work on the premise that favourable pericyclic reactions will proceed via an aromatic transition state. There are in fact two basic kinds of relevant aromaticity that differ fundamentally in their symmetry/topological properties. Depending on whether the reaction is promoted by heat or light (Δ or hν) we can divide the rules into a total of five categories.
Thermal (closed shell electronic state) with ~plane of symmetry/suprafacial and no twist: Hückel Aromaticity and Lk=0.
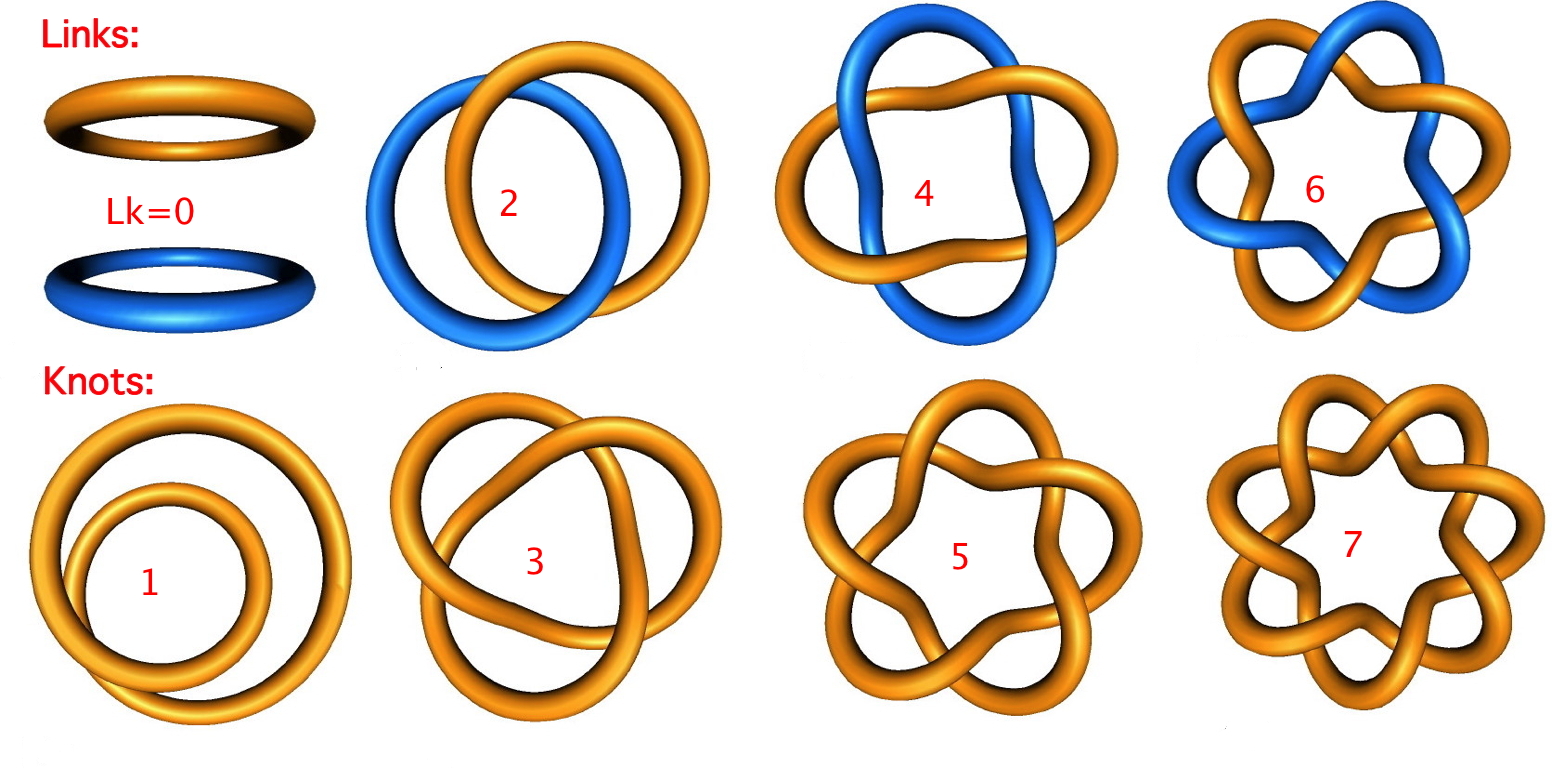
The suprafacial mode orbital correlation diagram for hexatriene can be generalised by reference to benzene, the archetypical aromatic molecule. The benzene molecule has suprafacial π-conjugation, deriving from a plane of symmetry. This means that the π-electron density in benzene is cyclically continuous along either the top OR the bottom face of the molecule and reflects symmetrically in a plane of symmetry bisecting the benzene. In mathematics, this type of topological object is more generally known as a two component torus link‡ with a linking number Lk of zero.
Benzene is particularly stable (=aromatic) because the cyclically conjugated π electrons all occupy stable doubly-filled molecular orbitals for which the total π-electron count conforms to the equation 4n+2; the Hückel rule, where n = 0, 1, 2 etc (a rule incidentally not actually formulated by Hückel but by the organic chemist William von Doering, see DOI: 10.1021/ ja01146a537).

If the transition state for the pericyclic reaction has the same π-electron density suprafacial topology, it is said to be a Hückel system. This is in honour of Erich Hückel who first indicated why a molecule such as benzene should be especially stable (and also, as it happens, was also the first to formalise the separation of σ and π electrons). It follows the same 4n+2 rule as for benzene, but this time counting the electrons involved in the reaction rather than just the π-electrons in the aromatic ring.
The advantage of this approach is that aromaticity is quite stable to perturbations to the symmetry (benzene rings in e.g. cyclophanes for example can be bent by up to 30° and still retain their aromaticity as evidenced by e.g. NMR).
So we conclude: closed shell pericyclic reactions will proceed all suprafacially via Hückel stereochemistry if the electron count corresponds to 4n+2. Hence this rule can now be applied to unsymmetric pericyclic reactions, which of course are by far the most common.
Student question: Can a transition state be so stabilised (by aromaticity) that it becomes an intermediate in its own right?
A: See 
Photochemical (open shell) with ~plane of symmetry/suprafacial and no twist: Hückel Aromaticity and Lk=0
Some time after Hückel, it was shown that the excited (triplet) electronic state of cyclic suprafacially conjugated π system created by (photochemically) promoting one electron from a doubly occupied orbital into a higher energy molecular orbital to produce what is called an open shell molecule is associated with aromaticity only if the π-electron count is 4n rather than 4n+2. An example of such an open shell aromatic molecule is the triplet state of cyclobutadiene.
Applying the same analogy as before, we infer that open shell pericyclic reactions (which normally means photochemically activated) will proceed suprafacially via Hückel stereochemistry if the electron count corresponds to 4n. The most modern approach does not use transition states to infer the stereochemistry for the photochemical reactions, but another feature in the potential energy surface(s) known as the conical intersection, with normally the same stereochemical conclusion. 
Thermal (closed shell electronic state) with 1 twist (axis of symmetry/one antarafacial mode): Möbius Aromaticity and Lk=1
 The antarafacial stereochemical mode associated with the orbital correlation diagrams is said to resemble Möbius topology, after August Ferdinand Möbius, who invented the famous strips (as did Johann Benedict Listing). An antarafacial mode can be formed by taking a cyclic alkene "strip" and giving its π-electron system a 180° (half) twist (and in doing create a two-fold axis of symmetry in the resulting molecule). Edgar Heilbronner in 1964 speculated theoretically (no such molecules were then known) that such a twisted system would be a closed shell molecule if it contained 4n conjugated π electrons doubly occupying 2n MOs. It was later shown that it would also be aromatic! It is very recently recognized (DOI: 10.1039/b810301a) that topological analysis of the electron density derived from these 4n-electrons indicates it to be a topological object known as a single-component torus knot‡, with a linking number Lk of one (the specific name of such a knot is actually an unknot). As might be expected of an object with only a two-fold (C2) axis of symmetry, it has disymmetric chirality.
The antarafacial stereochemical mode associated with the orbital correlation diagrams is said to resemble Möbius topology, after August Ferdinand Möbius, who invented the famous strips (as did Johann Benedict Listing). An antarafacial mode can be formed by taking a cyclic alkene "strip" and giving its π-electron system a 180° (half) twist (and in doing create a two-fold axis of symmetry in the resulting molecule). Edgar Heilbronner in 1964 speculated theoretically (no such molecules were then known) that such a twisted system would be a closed shell molecule if it contained 4n conjugated π electrons doubly occupying 2n MOs. It was later shown that it would also be aromatic! It is very recently recognized (DOI: 10.1039/b810301a) that topological analysis of the electron density derived from these 4n-electrons indicates it to be a topological object known as a single-component torus knot‡, with a linking number Lk of one (the specific name of such a knot is actually an unknot). As might be expected of an object with only a two-fold (C2) axis of symmetry, it has disymmetric chirality.
The first explicit example of a Möbius molecule was suggested in 1998 as being the cation C9H9+ (which has 8 cyclically conjugated π-electrons). It is a 4n system, where n=2 and its 1H NMR suggested it was indeed aromatic, from which it was inferred as being Möbius. In 2003, a crystalline Möbius annulene was first made (DOI: 10.1021/cr030092l) and the axis of symmetry was finally revealed. Quite a number of Möbius systems have been identified from 2006 onwards.
So, using the same analogy as before, thermal pericyclic reactions will proceed with one antarafacial component via a Möbius aromatic transition state if the electron count corresponds to 4n.
Photochemical (open shell) with 1 twist (axis of symmetry/one antarafacial mode): Möbius Aromaticsity and Lk=1
Just as photochemical (excited state) Hückel systems conform to a 4n-electron rule, so photochemical Möbius systems conform to a 4n+2-electron rule. As before, we nowadays use a conical intersection rather than a transition state geometry to infer the rule using quantum mechanics.
Systems with 2 or more twists (axes of symmetry/more than one antarafacial mode): Higher order Möbius Aromaticity (Lk > 1).
In 2005, it was realised that topological objects with two twists were also interesting. Whilst largely beyond the scope of these lectures, it is worth noting here that two twists in cyclically conjugated π-electrons give a Möbius aromatic molecule which again conforms to the 4n+2 rule, but this time the molecule has disymmetric chirality which is associated not with a plane of symmetry but with (three or more) axes. Its electron density gives rise to a topological object known as a torus link with linking number Lk of 2‡. The chemistry of chiral aromatic molecules (before 2005 regarded as a chemical oxy-moron) is now rapidly expanding and around 30-40 molecules with these features are known. And again, one can draw an analogy with pericyclic transition states. This will exhibit two antarafacial components (the number of these are formally equal in value to the linking number). For (optionally) more details, see here or the blog.
(This approach is optional and is intended for use in tutorials). This involves using the principles of quantum mechanics to generate the Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO) for the reactant(s). The formation of the new σ bond must occur by appropriate overlap of the nodes of these orbitals. If only one σ bond is forming, as in an electrocyclic reaction, then only the overlap of the HOMO of the reactant is considered. Such overlap can occur in one of two fundamental ways; The suprafacial mode involves each component of the new σ bond being formed from the SAME face of the reactant π system. See DOI: 10.1016/S0040-4039(01)83901-0.
The antarafacial mode involves a 'twisting' of the orbitals so that the two components of the new σ bond come from OPPOSITE faces of the reactant π system. If two or more σ bonds form during the reaction, as in cycloaddition reactions, then the overlap of the HOMO of one reactant with the LUMO of the second reactant must be considered. For simple systems, the form of the HOMO and LUMO is not difficult to remember. For more complex systems, explicit calculations have to be carried out and the Frontier Orbital method becomes more difficult to apply. The advantage of the "FMO" method is that it can be expressed quantitatively in terms of the magnitude of the coefficients involved, and can hence be used to predict regioselectivity etc.
 The next level of theory beyond the FMO method involves the explicit location of the pericyclic:
The next level of theory beyond the FMO method involves the explicit location of the pericyclic:
using quantum mechanical potential energy surfaces and dynamics. You will get a chance to try this out in 3rd year computational labs.
‡The first attempt to theoretically derive the periodic table of elements was made in 1867 and was based on knots, not quantum mechanics which of course had not yet been invented! Even more spooky, knots are now the basis of string theory, which attempts to explain the inner structure of all fundamental particles. Explore links and knots here or here.
© Henry S. Rzepa, 1978-2014. Hide|show Toolbar.