| [Related articles/posters: 050 033 120 ] |
INTRODUCTION
We have been interested in studying the linear and nonlinear optical
properties of crystals of N-perturbed donor-acceptor
asymmetrized conjugated systems of the azine type. We have systematically
studied the crystal structures and the packing of symmetric
[1,
2], and
asymmetric
[3,
4,
5], acetophenone azines. These
acetophenone azines have
the general formula X-Ph-C(Me)=N-N=C(Me)-Ph-Y and they are called
symmetric if X = Y and asymmetric if X and Y are different. Our studies
have resulted in the first realization of two prototypes of molecular
organic materials with near-perfect dipole parallel-alignment in the pure
crystal of 4-bromo- and 4-chloro-4'-methoxyacetophenone azines
[3,
4,
6,
7].
The de novo design of crystals is an undertaking of extraordinary
difficulty since the lattice architecture results from the optimization of
a large number of weak intermolecular interactions. The interactions are
too complex to trace and the computation of lattice energies still
presents a formidable challenge [8].
Arene-arene interactions are central
to the crystal lattice architectures of the acetophenone azines. The
crystal structures of the prototypes of the piezoelectric azines show
pairs of perfectly parallel aligned azine molecules with two T-contact
arene-arene interactions. The Ph-CR=N-N=CR-Ph system thus constitutes a
"double T-contact synthon" and we believe this motif to be key to
understanding the suprastructures of the prototypes. Double T-contacts
occur when the arene rings of two compounds containing two arene groups
each stack in such a way that two edge-to-face arene-arene contacts are
realized [9].
One strategy to increase the lattice energies of crystals of acetophenone
azines aims at strengthening the arene-arene contacts. The components of
the quadrupole moment tensor associated with an arene can be effected by
placing substituents on the aromatic ring. The computed quadrupole moments
of benzene and hexafluorobenzene are given in Table 1 and this data
demonstrates in a compelling fashion that polyfluorination is a
particularly promising strategy to increase quadrupolarity; the quadrupole
moment of hexafluorobenzene is essentially twice as large as that of
benzene.
|
Quadrupole Component |
Benzene RHF |
Benzene MP2(fc) |
C6F6
RHF |
C6F6 MP2(fc) |
| Qxx = Qyy | -31.3833 | -31.6337 | -68.7893 | -70.9189 |
| Qzz | -39.7335 | -40.7407 | -59.3556 | -60.3562 |
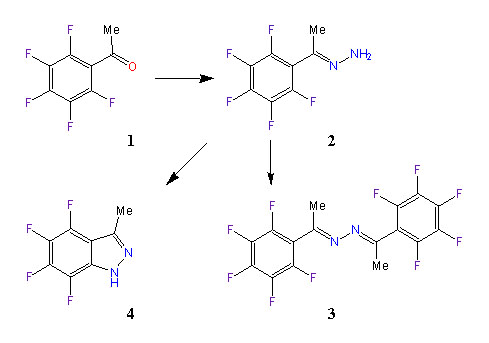
In this context, we wanted to prepare the symmetrical azine 3 from 2,3,4,5,6-pentafluoroacetophenone 1 via the hydrazone 2. However, no azine is formed when 1 was heated with hydrazine in toluene and it was found that 3-methyl-4,5,6,7-tetrafluoro-1H-indazole, 4, was formed instead. The molecular formula of the indazole 4 was verified via high resolution mass spectrometry. The confirmation of the structural formula of 4 via single crystal X-ray analysis was attempted but the fibrous nature of the material precluded the growing of suitable crystals. The structure of indazole 4 was supported by comparing the measured 1H-, 13C-, and 19F-NMR spectra to the results of ab initio GIAO computations of chemical shifts. We also report the ab initio optimized structure of the parent indazole and of 4 and a comparative analysis of their electronic structures in terms of molecular and atomic properties.
EXPERIMENTAL AND COMPUTATIONAL SECTION
Preparation
To a solution of 1 (2.10 g, 10.0 mmoles) in 10 mL of toluene were added 0.5 mL (10 mmoles) of hydrazine hydrate. The reaction mixture was heated at reflux overnight and a solid precipitate formed. The precipitate (0.41 g) was filtered and washed with toluene. The toluene filtrate was rotary evaporated to yield a yellowish solid, which was recrystallized from ethanol-water to yield 0.40 g of a white fibrous solid. Spectroscopy was used to ascertain that the first precipitate and the recrystallized solid were identical.
NMR Spectroscopy and Mass Spectrometry
The NMR spectra were recorded with a Bruker DPX-300 NMR spectrometer with spectrometer frequencies of 300.13 MHz for H-NMR, 75.48 MHz for 13C-NMR, and 282.40 MHz for 19F-NMR. A 5 mm broadband probe was used.
1H-NMR (CDCl3, standard TMS): 11.60 ppm (1H, broad singlet, NH), 2.57 ppm (3H, singlet, CH3).
13C-NMR (DMSO, standard TMS): 140.1 ppm (m, C(3)), 138.6 ppm (ddt, J = 249 Hz, J' = 15 Hz, J" = 4Hz, C(4) or C(6)), 137.9 ppm (dtd, J = 234 Hz, J' = 13 Hz, J" = 3Hz, C(4) or C(6)), 133.3 ppm (dt, J = 241 Hz, J' = 15 Hz, C-5), 132.3 ppm (ddm, J = 249 Hz, J' = 16 Hz, C-7), 127.8 ppm (m, J = 8 Hz, C(7a)), 108.6 ppm (dd, J = 19 Hz, J' = 4 Hz, C(3a)), 12.6 ppm (s, CH3).
19F-NMR (DMSO, standard CFCl3): -150.5 ppm (m), -158.6 ppm (m), -160.3 ppm (m), -169.6 ppm (m).
Mass Spectrometry. EIMS (m/z): 408.0 (7.3), 208.0 (7.4), 204.9 (9.0), 203.9 (M+, 100.0), 203.0 (70.6), 200.0 (10.5), 176.0 (18.6), 162.0 (7.5), 149.0 (8.7), 68.9 (5.6). HR EIMS calculated for C8H4N2F4: 204.03105. Found: 204.03171.
Computational Section
Indazole is a planar molecule. Assuming Cs symmetry, two geometric conformers of the indazole 4 were recognized as possible energetic minima and these differed as to whether the methyl hydrogens are eclipsed or staggered with respect to the C=N double bond of the five-membered ring.
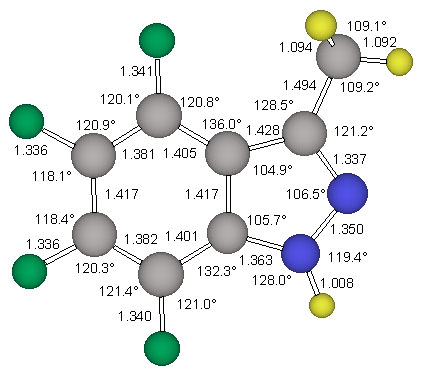
The geometries if both conformers of the derivative 4 were optimized at the restricted Hartree-Fock level of theory using the 6-31G* basis set (RHF/6-31G*) to determine the structure of lowest energy. A normal mode analysis was then carried out at the same level of theory to determine vibrational zero point energies as well as to characterize the structures as minima or saddle points. The RHF/6-31G* optimized structures of 4 are shown in Figure 4.
The 6-31G* basis set with a split-valence and polarization functions added to first-row atoms was first developed by Hariharan and Pople [10] and subsequently extended to second-row and heavier atoms by Francl et al. [11]. This basis set was chosen due to the need to treat polar bonds in the molecule adequately, while a larger basis set was not deemed necessary for characterization of the conformers. Hartree-Fock theory, which ignores electron correlation, was chosen to characterize the conformers. This method was chosen for efficiency reasons and because RHF calculations generally give good results at stationary points. Furthermore, RHF/6-31G* calculated frequencies can be scaled to fit experiment and higher level calculations with good accuracy [12].
A higher level geometry reoptimization and energy calculation was performed on the minimum energy structure found at the RHF/6-31G* level. Electron correlation was included using Moeller-Plesset perturbation theory truncated at second-order, designated MP2. Moeller-Plesset perturbation theory [13] treats instantaneous electron correlation effects as a perturbation to the Hartree-Fock Hamiltonian using a many-body Rayleigh-Schroedinger perturbation series expansion. Due to the size of the molecule, computational expense was a consideration and the frozen-core approximation was used, excluding all excitations of core electrons from the MP2 correlation calculation. MP2 correlation calculations using a frozen core are designated MP2(fc).
The 6-311G** basis set presented by Krishnan et al. [14] was used for the reoptimization of the minimum energy structure ecl-4. The triply-split valence basis set allows greater flexibility in the valence region, reducing basis set truncation errors in the description of bonding. This improved valence description is viewed as being especially important in the study of molecules containing multiple and delocalized bonding systems. The 6-311G** basis set also improves the treatment of X-H polar bonds by explicitely adding p-type basis functions to hydrogen atoms. Furthermore, the use of this basis set for the MP2 calculations is deemed to be a good choice when we note that the 6-311G** Gaussian exponents and contraction coefficients were optimized at this same level of theory. The MP2(fc)/6-311G** optimized structures of the parent indazole and of ecl-4 are shown in Figure 3 and Figure 5, respectively.
A Natural Bond Orbital (NBO) population analysis [15], which localizes the many-electron wavefunction into Lewis-type electron-pairs of bonding, non-bonding and anti-bonding types, was carried out at the MP2(fc)/6-311G** level of theory to determine natural atomic charges.
Finally, an NMR analysis was performed on the MP2(fc)/6-311G** optimized structure. This required the calculation of isotropic shielding tensors of the atoms in the indazole as well as in the reference molecules (TMS for 1H- and 13C-NMR, CFCl3 for 19F-NMR, and CH3NO2 for 14/15N-NMR). The difference between the calculated shielding tensors gives the chemical shifts. The Gauge-Invariant Atomic Orbital (GIAO) method [16 - 20] was used to calculate the shielding tensors at the B3LYP/6-311+G* level of theory. Electron correlation was included in the NMR calculations by use of density functional theory (DFT) because of its reported accuracy and its availability for GIAO calculations in the Gaussian 94 suite of programs [21].
The B3LYP functional was used, which combines Becke's three parameter exchange functional [22] with the correlation functional of Lee, Yang and Parr [23, 24]. These are both non-local functionals whose combination is widely used and accepted. The 6-311+G* basis set is similar to that used for reoptimization of the minimum structure, while sacrificing the polarization functions on hydrogen atoms for diffuse functions of the valence type on heavy atoms.
All calculations were performed using the Gaussian 94 package [21] on a Silicon Graphics Power Challenge-L computer at the University of Missouri-Columbia.
RESULTS AND DISCUSSION
Preparation of 3-Methyl-4,5,6,7-tetrafluoro-1H-indazole
The azine of pentafluorobenzaldehyde had been previously prepared by stirring pentafluorobenzaldehyde with hydrazine in water at room temperature [25] and we intended to prepare the symmetrical azine 3 from 2,3,4,5,6-pentafluoroacetophenone 1 via the hydrazone 2 in a similar fashion (Scheme 1). However, no azine was formed when this procedure was attempted with the acetophenone 1 due to the insolubility of 1 in water. When 1 was heated with hydrazine in toluene, a reaction occured and a white precipitate formed. The product was crystallized from ethanol-water. Examination of the proton-decoupled 13C-NMR spectrum of the product indicated that neither the hydrazone nor the azine had been produced. The 19F-NMR spectrum showed only 4 sets of peaks. These data suggested that 3-methyl-4,5,6,7-tetrafluoro-1H-indazole, 4, had been formed. The indazole was probably formed via the hydrazone 2 which cyclized via the displacement of an ortho fluorine by the amino group to form 4. Polyfluorinated aromatic compounds readily undergo nucleophilic aromatic substitution by a variety of nucleophiles [26]. For example, when 2-(pentafluorophenyl)ethanamine is heated at reflux in DMF, 2,3-dihydro-4,5,6,7-tetrafluoroindole is formed by intramolecular displacement of a fluorine by the amine nitrogen [27]. Precedent for the formation of indazoles via the nucleophilic substitution of halogens by hydrazine amino groups in 2-halogeno-1-(1-hydrazono-alkyl)-arenes has been presented in Stadlbauer's recent review of indazole chemistry [28a]. The replacement of fluorine by hydrazine followed by pyrazole ring formation also presents a mechanistic possibility [28b].
The 19F- and 13C-NMR spectra of indazole 4 are shown in Figures 1 and 2. The assignments will be made below on the basis of ab initio computations of chemical shifts.
Ab InitioStudy of 3-Methyl-4,5,6,7-tetrafluoro-1H-indazole
There have been only relatively few quantum-mechanical studies of indazoles at the semi-empirical level [29, 30] or at the ab initio level [31, 32, 33] and the ab initio studies that were reported have been limited to Hartree-Fock level theory with small to modest basis sets.
One of the earliest ab initio studies of indazole is the 1988 paper by Hodoscek et al. [31]. This study employed a minimal basis set, RHF/STO-3G, and showed a preference for the 1H-tautomer.
In 1992, Velino et al. [32] reported the microwave spectrum of the parent indazole together with RHF/4-21G calculations. Again, experiment and theory both clearly show a preference for the 1H-tautomer. The bond lengths of the RHF/4-21G computed structure was found to be somewhat underestimated (less than 0.02 Ang.) and our calculations will show whether this underestimation is dues to basis set trunction or to the neglect of elecron correlation or both. Interestingly, and most pertinent for the present study, the authors succeeded in measuring the dipole moment of indazole and reported a value of 1.76(2) Debye.
Recently, Williams and Whitehead [33] presented an extensive comparison between heats of formation of aromatic nitrogen heterocyclics computed with semi-empirical (MNDO, AM1, PM3) and ab initio (RHF/4-31G and RHF/6-31G**) methods. The heat of formation of indazole was reported to be 62.4 kcal/mol. No structures or properties were reported.
Geometry and Conformational Preference
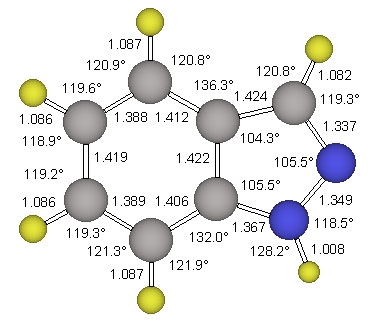
The parent indazole and two conformers of 4, ecl-4 and stag-4, were examined in Cs-symmetry. All structures were optimized at the RHF/6-31G* level of ab initio molecular orbital theory. Vibrational frequency analyses were carried out analytically to confirm that the gradient optimizations had indeed converged, to characterize the stationary structures and to obtain vibrational frequencies and thermochemical data. The parent indazole and the minimum structure ecl-4 were also refined at the MP2(fc)/6-311G** level. Pertinent energy data are summarized in Table 2 together with the electrostatic properties. The structure of the parent indazole is shown in Figure 3.
Molecule |
Indazole | Indazole |
Transition State stag.-4 |
Minimum ecl.-4 |
Minimum ecl.-4 |
| Theoretical Level |
RHF | MP2(fc) | RHF | RHF | MP2(fc) |
| Eelectronic [Hartree/Particle] |
-377.446718 | -378.829263 | -811.859482 | -811.861256 | -814.292070 |
| Vibr. Zero Point Energy (VZPE) [Hartree/Particle] |
0.116313(b) | - | 0.111612(b) | 0.111745(b) | - |
| Eelec. +
scaled RHF VZPE [Hartree/Particle] |
-377.330405 | -378.712953 | -811.747870 | -811.749511 | -814.180325 |
| Dipole Moment [Debye] | 1.8200 | 1.8445 | 2.0832 | 2.0503 | 2.4117 |
| Qxx [Debye-Ang.] | -53.0281 | -53.5479 | -78.1329 | -78.0733 | -78.6908 |
| Qyy [Debye-Ang.] | -41.2500 | -41.4180 | -82.0096 | -82.2362 | -83.1602 |
| Qzz [Debye-Ang.] | -56.1135 | -57.3164 | -75.4210 | -75.4483 | -76.5024 |
| Qxy [Debye-Ang.] | +3.2311 | +3.2776 | -3.8685 | -3.8118 | -3.8728 |
The structure stag-4 was found to exhibit one imaginary frequency (i 139 1/cm) and the associated normal mode identifies this structure as the transition state for methyl rotation. The structure ecl-4 is the minimum and all its vibrational frequencies are real. The activation barrier for this methyl rotation is only about 1.03 kcal/mol (Table 2). The structure of the minimum ecl-4 was refined at the correlated level MP2(fc)/6-311G** and the resulting geometry is shown in Figure 5.
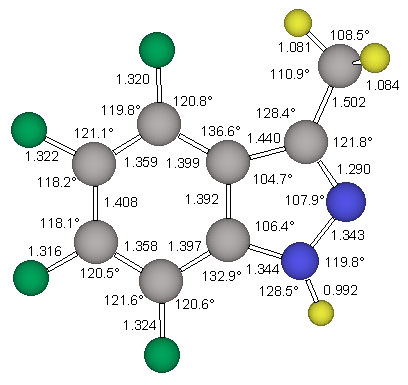
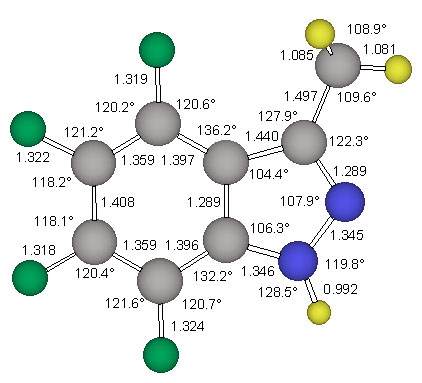
NMR Chemical Shift Assignments
We have computed the isotropic shielding tensors for all atoms in indazole and in ecl-4 using density functional theory at the level B3LYP/6-311+G(2d,p) and based on the MP2(fc)/6-311G** optimized structure. These data were converted into chemical shifts and the resulting data are summarized in Table 3.
The computed data allow an assignment of the data measured for ecl-4. The computed and experimental data do not match in absolute terms. The computed carbon chemical shifts all are overestimated (by 3.3 - 12.4 ppm) while all the fluorine chemical shifts are underestimated (by 12.9 - 20.4 ppm) and there is considerable variation between individual deviations. In most cases, the peak separations are of such a magnitude that the assignments based on relative chemical shifts appear reliable. An exception are C4 and C6 for which nearly identical chemical shifts are computed and either of the peaks at 137.9 and 138.6 ppm could be due to either of these C-atoms. In this case, however, the splitting patterns due to CF-coupling allow one to differentiate between the two C-atoms.
|
Scheme 2. Atom numbering according to the IUPAC nomenclature. |
| Molecule | Indazole | ecl-4 | ecl-4 | ecl-4 |
| Atom |
Chemical Shift calculated [ppm] |
Chemical Shift calculated [ppm] |
Chemical Shift measured [ppm] |
Chemical Shift deviation [ppm] |
| C(3) | +141.44 | +152.51 | +140.1 (A) | -12.4 |
| C(3a) | +130.79 | +115.68 | +108.6 (G) | -7.1 |
| C(4) | +126.40 | +149.77 | +138.5 (C) | -11.3 |
| C(5) | +126.92 | +145.11 | +133.3 (B) | -11.8 |
| C(6) | +131.99 | +149.79 | +137.9 (D) | -11.9 |
| C(7) | +113.45 | +141.39 | +132.3 (E) | -9.1 |
| C(7a) | +146.37 | +133.06 | +127.8 (F) | -5.3 |
| H-C(3) / C-C(3) | +8.28 | +15.92 | +12.6 | -3.3 |
| X-C(4) (X=H,F) | +8.05 | -163.35 | -150.5 | 12.9 |
| X-C(5) (X=H,F) | +7.49 | -182.68 | -169.6 | 13.1 |
| X-C(6) (X=H,F) | +7.69 | -171.77 | -158.6 | 13.2 |
| X-C(7) (X=H,F) | +7.68 | -180.71 | -160.3 | 20.4 |
| N(1) | -218.80 | -229.68 | not measured | - |
| N(2) | -66.98 | -69.67 | not measured | - |
| Hip | - | +2.80 | +2.57 | -0.23 |
| Hoop | - | +2.70 | +2.57 | -0.13 |
| H-N(1) | +9.59 | +9.33 | +11.60 (broad) | 2.27 |
Electronic Structure: Charges, Dipoles & Quadrupoles
There have been only two semi-empirical studies that concerned themselves with the charge distribution in the parent indazole. Catalan et al. [29] reported an INDO study and gave YSP charges and Escande et al. [30] reported Mulliken charges determined at the CNDO level. Computed charge distributions of the parent and fluorinated indazole were used to examine the effect of fluorination of the six-membered ring. The dipoles and quadrupole moments are tabulated in Table 2, while Table 4 displays atomic charges for both molecules.
The semi-empirical CNDO and INDO atomic charges were included in Table 4 for comparison and it can be seen that they do not agree in more than a rough qualitative fashion with our calculated natural charges at the MP2(fc)/6-311G** level of theory. For this reason, we will only discuss the atomic charges computed at the higher ab initio level of theory.
The effect of fluorination of the indazole can be seen most dramatically in the atomic charges of carbon atoms C(4) through C(7), those which are fluorinated. These carbons bear a slight negative charge in the parent indazole, while having a strong positive character when the hydrogens are replaced by fluorine atoms. The reason for this is easily explained by the strong inductive electron withdrawing ability of fluorine atoms. The only other large discrepancy in charges is the amount of positive character on C(3). However, this change cannot be attributed to fluorination of the molecule, but more so to the presence of the C(3)-methyl group on the fluorinated indazole.
Probably the most striking result is the unexpectedly small change in the magnitude of the dipole moment upon fluorination. At the RHF level of theory, the dipole moment is only 0.2632 Debye higher in the fluorinated species than in the parent indazole. Inclusion of electron correlation effects at the MP2(fc) level increases this difference to 0.5672 but the dipole increase remains rather small despite the high electronegativity of fluorine. However, the direction of the dipole is changed quite significantly (see Scheme 3). The dipole moment of the parent indazole lies on an axis approximately through C(3) and C(6). Fluorination adds an almost equal component to the dipole moment along a perpendicular axis in the plane of the indazole.
The change in the direction of the dipole associated with fluorination of the indazole can be explained in terms of electronegativities and bond polarizabilities. The fluorination of the six-membered ring leads to partial positive charges on the carbons to which the F-atoms are attached, atoms C(4), C(5), C(6) and C(7). The electron depletion on these atoms causes a polarization through the sigma framework and draws electron density from the five-membered ring. This electron density could be transfered through either the C(7a)-N(1) or the C(3a)-C(3) bond. Due to the higher electronegativity of nitrogen with respect to carbon, one would expect the C(3a)-C(3) bond to be more polarizable that the C(7a)-N(1) bond. In fact, this is what we see in the NBO natural charges. The fluorination of the indazole polarizes the C(3a)-C(3) bond, resulting in a larger positive charge on C(3) and a build-up of negative charge on C(3a), while the charges on C(7a) and N(1) are virtually unaffected. This rearrangement of electron density explains the change in direction of the molecular dipole upon fluorination, shown in Scheme 3.
To understand the indazole quadrupole moments, we must first consider the calculated quadrupoles of benzene and hexafluorobenzene (Table 1). Both of these molecules have all negative components to their quadrupoles, that is the charge distributions are of the type (-)-(+)-(-). The negative Qzz component is easily explained. The negative charge distributions above and below the ring are the result of the pi-clouds of the aromatic rings, while there is a positive distribution associated with the ring of C-atoms in the z-plane. Fluorination of the ring enhances this effect by withdrawing electron density from the carbons and increasing the positive charge on the ring. The negative Qxx and Qyy tensor components are more difficult to explain. These components are equal because of the symmetry of benzene, but the hydrogens do not bear enough negative charge to explain the magnitude of the quadrupole. However, one must realize that the bonds between the carbon and hydrogen atoms distort the electron density around the atoms. Sigma bonding will polarize the carbon atoms' electron densities towards the hydrogens, resulting in a partial negative charge on the outside of the carbon skeleton and a partial positive charge inside the benzene ring. The magnitude of these quadrupole components is increased upon fluorination because of the greater electronegativity of fluorine and, hence, a greater distortion of the electron density surrounding the carbon atoms. The F-C bonds are also fairly polar and will result in a significant negative charge on the fluorines, further increasing the magnitude of the Qxx amd Qyy quadrupole components.
The quadrupole components given in Table 2 for the parent and fluorinated indazoles show the same trends as those in benzene and hexafluorobenzene. The Qxx, Qyy and Qzz components are all negative and their magnitudes are increased dramatically when the six-membered ring is fluorinated. However, the asymmetry of the molecule results in slightly different Qxx and Qyy components as well as a non-zero Qxy contribution to the quadrupole. One should note that, due to their non-zero dipoles, the indazole quadrupoles are dependent on the origin chosen for their calculation. The quadrupoles reported in Table 2 are calculated using standard orientation of the molecules, which places the origin at the center of nuclear charge.
| Molecule | Indazole | Indazole | Indazole | ecl-4 |
| Atom |
CNDO Mulliken Charge |
INDO YSP Charge |
MP2(fc) Natural Charge |
MP2(fc) Natural Charge |
| C(3) | +0.0705 | +0.184 | +0.0368 | +0.2328 |
| C(3a) | -0.0432 | +0.039 | -0.1771 | -0.2263 |
| C(4) | +0.0301 | +0.097 | -0.1307 | +0.4578 |
| C(5) | -0.0297 | +0.058 | -0.2342 | +0.3105 |
| C(6) | +0.0269 | +0.087 | -0.1491 | +0.3859 |
| C(7) | -0.0441 | +0.050 | -0.2440 | +0.3591 |
| C(7a) | +0.1198 | +0.228 | +0.2045 | +0.1581 |
| H-C(3) / C-C(3) | -0.0101 | -0.010 | +0.1894 | -0.5328 |
| X-C(4) (X=H,F) | -0.0129 | -0.021 | +0.1944 | -0.3727 |
| X-C(5) (X=H,F) | -0.0077 | -0.023 | +0.1914 | -0.3662 |
| X-C(6) (X=H,F) | -0.0103 | -0.025 | +0.1907 | -0.3625 |
| X-C(7) (X=H,F) | -0.0023 | -0.014 | +0.1978 | -0.3729 |
| N(1) | -0.0878 | -0.429 | -0.4068 | -0.4010 |
| N(2) | -0.1001 | -0.393 | -0.2652 | -0.2712 |
| Hip | - | - | - | +0.2015 |
| Hoop | - | - | - | +0.1917 |
| H-N(1) | +0.1009 | +0.170 | +0.4023 | +0.4166 |
Acknowledgments
This research was supported by grants from the Research Council and the Research Board of the University of Missouri and by the National Science Foundation ILI program and the National Aeronautics and Space Administration Joint Venture program. Graeme Day is the recipient of a Huggins Fellowship. Michael Lewis holds a Natural Sciences and Engineering Research Council of Canada, post-graduate scholarship, type A, tenable abroad. We want to thank Professor Wolfgang Stadlbauer for valuable comments.
References
1. (a) G. S. Chen, M. Anthamatten, C. L. Barnes and R. Glaser,
J. Org. Chem., 59, 4336 (1994);
(b) G. S. Chen, M. Anthamatten, C. L. Barnes and R. Glaser,
Angew. Chem. Int. Ed. Engl., 33, 1081, (1994);
(c) R. Glaser, G. S. Chen and C. L. Barnes,
J. Org. Chem., 58, 7446 (1993).
2. R. Glaser, G. S. Chen, M. Anthamatten and C. L. Barnes,
J. Chem. Soc. Perkin Trans. 2, 1449 (1995).
3. G. S. Chen, J. K. Wilbur, C. L. Barnes and R. Glaser,
J. Chem. Soc., Perkin Trans. 2, 2311 (1995).
4. R. Glaser and G. S. Chen,
Poly. Mat. Sci. Eng., 75, 229 (1996).
5. R. Glaser and G. S. Chen,
J. Comput. Chem., 19, xxx (1998).
6. The piezoelectric material 4-bromo-4'-methoxyacetophenone azine has
been featured as the
Molecule
of the Month for December 1997.
7. Crystal structure of the organic piezoelectric
4-chloro-4'-methoxyacetophenone azine. R. Glaser, M. Lewis and C. L.
Barnes. In preparation.
8. D. Steiger, C. Ahlbrandt and R. Glaser,
J. Phys. Chem. B, 102, 4257 (1998).
9. M. Lewis, C. Barnes and R. Glaser,
Can. J. Chem., submitted.
10. P.C. Hariharan and J. A. Pople,
Theor. Chim. , 28, 213 (1973).
11. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon,
D. J. DeFrees and J. A. Pople,
J. Chem. Phys., 77, 3654 (1982).
12. J. A. Pople, A. P. Scott, M. W. Wong and L. Radom,
Isr. J. Chem., 33, 345 (1993).
13. C. Moeller and M. S. Plesset,
Phys. Rev., 46, 618 (1934).
14. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople,
J. Chem. Phys., 72, 650 (1980).
15. NBO Version 3.1, E. D. Glendening, A. E. Reed, J. E. Carperter, and F.
Weinhold.
16. K. Wolinski, J. F. Hilton and P. Pulay,
J. Am. Chem. Soc., 112, 8251 (1990).
17. J. L. Dodds, R. McWeeny and A. J. Sadlej,
Mol. Phys., 41, 1419 (1980).
18. R. Ditchfield, Mol. Phys., 27, 789 (1974).
19. R. McWeeny, Phys. Rev., 126, 1024 (1962).
20. F. London, J. Phys. Radium, Paris, 8, 397
(1937).
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B.
G. Johnson, M. A. Robb, J. R. Cheeseman, T. Keith, G. A. Petersson,
J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski,
J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov,
A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen,
M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin,
D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M.
Head-Gordon, C. Gonzalez and J. A. Pople, Gaussian 94, Revision C.3;
Gaussian Inc.: Pittsburgh, PA. 1995.
22. A. D. Becke, J. Chem. Phys., 98, 5648 (1993).
23. C. Lee, W. Yang and R. G. Parr,
Phys. Rev. B, 37, 785 (1988).
24. B. Miehlich, A. Savin, H. Stoll and H. Preuss,
Chem. Phys. Lett., 157, 200 (1989).
25. E. V. Aroskar, P. J. N. Brown, R. G. Plevey and R. Stephens,
J. Chem. Soc. (C), 1569 (1968).
26. G. G. Yacobson and V. M. Vlasov,
Synthesis, 652 (1976).
27. I. L. Knunyants and G. G. Yakobson, Eds.,
Syntheses of Fluoroorganic Compounds. Springer-Verlag: Berlin, 222
(1985).
28. W. Stadlbauer, Indazole (Benzopyrazole), in Houben-Weyl,
Methoden der Organischen Chemie, Volume E8b, Hetarenes
III/2, p. 764-864, Georg Thieme Verlag, Stuttgart, 1994.
(a) p. 786.
(b) p. 796.
29. J. Catalan, O. Mo, P. Perez and M. Yanez,
J. Mol. Struct., 94, 143 (1983).
30. A. Escande, J. Lapasset, R. Faure, E.-J. Vincent and J. Elguero,
Tetrahedron, 30, 2903 (1974).
31. (a) D. Kocjan, M. Hodoscek and D. Hadzi,
J. Mol. Struct. (Theochem), 152, 331 (1987).
(b) M. Hodoscek, D. Kocjan and D. Hadzi,
J. Mol. Struct. (Theochem), 165, 115 (1988).
32. B. Velino, W. Cane, A. Trombetti, G. Corbelli, F. Zerbetto and W.
Caminati,
J. Mol. Spectr., 155, 1 (1992).
33. C. I. Williams and M. A. Whitehead,
J. Mol. Spectr. (Theochem), 393, 9 (1997).