In this post, I will take a look at what must be the most extraordinary small molecule ever made (especially given that it is merely a hydrocarbon). Its peculiarity is the region indicated by the dashed line below. Is it a bond? If so, what kind, given that it would exist sandwiched between two inverted carbon atoms?
One (of the many) methods which can be used to characterize bonds is the QTAIM procedure. This identifies the coordinates of stationary points in the electron density ρ(r) (at which point ∇ρ(r) = 0) and characterises them by the properties of the density Hessian at this point. At the coordinate of a so-called bond critical point or BCP, the density Hessian has two negative eigenvalues and one positive one. The sum, or trace of the eigenvalues of the density Hessian at this point, denoted as ∇2ρ(r), provides in this model a characteristic indicator of the type of bond, according to the following qualitative partitions:
- ρ(r) > 0, ∇2ρ(r) < 0; covalent
- ρ(r) ~0, ∇2ρ(r) > 0; ionic
- ρ(r) > 0, ∇2ρ(r) > 0; charge shift
The third category of bond was first characterised by Shaik, Hiberty and co. using valence-bond theory1 and they went on to propose [1.1.1] propellane (above, along with F2) as an exemplar of this type.2 Matching the conclusions drawn from VB theory was the value of the Laplacian. As defined above, for the central C-C bond, both ρ(r) and ∇2ρ(r) have been calculated to be positive, supporting the identification of this interaction as having charge-shift character.3
The Laplacian represents one of those properties where quantum mechanics meets experiment, in that its value (and that of ρ(r) itself) can be measured by (accurate) X-ray techniques.4 This was recently accomplished for propellane,5 with the same conclusion that the Laplacian in the central C-C region has the significantly positive value of +0.42 au. The electron density ρ(r) at this point was measured as 0.194 au. Calculations5 at the B3LYP/6-311G(d,p) level report ρ(r) as ~0.19 and ∇2ρ(r) as +0.08 au. Whilst the former is in good agreement with experiment, the latter is calculated as rather smaller than expected. This was originally interpreted as indicating that the “the experimental bond path has a stronger curvature [in ρ(r)] than the theoretical” although more recent thoughts are that both experimental and theoretical uncertainty may account for the discrepancy.5,6 An experiment worth repeating?
A hitherto largely unexplored aspect of characterising a bond using the Laplacian is whether the value at the bond critical point is fully representative of the bond as a whole. The Laplacian is related to two components of the electronic energy by the Virial theorem;
2G(r) + V(r) = ∇2ρ(r)/4; H(r) = V(r) + G(r)
where G(r) is the kinetic energy density, V(r) is the potential energy density and H(r) the energy density. Charge-shift bonds exhibit a large value of the (repulsive) kinetic energy density, a consequence of which is that ∇2ρ(r) is more likely to be positive rather than negative. The relationships above hold not just for the specific coordinate of a bond critical point, but for all space. Accordingly, another way therefore of representing the Laplacian ∇2ρ(r) is to plot the function as an isosurface, including both the negative surface (for which |V(r)| > 2G(r)) and the positive surface [for which |V(r)| < 2G(r)].
Such an analysis is the purpose of this post, using wavefunctions evaluated at the CCSD/aug-cc-pvtz level (see DOI: 10042/to-5012). The values of ρ(r) and ∇2ρ(r) at the bcp for the central bond are 0.188 and +0.095 au, which compares well with previous calculations. The values for the wing C-C bonds are 0.242 and -0.491 respectively (and were measured5 as 0.26 and -0.48). Laplacian isosurfaces corresponding to ± 0.49 (the value at the wing C-C bcp), ± 0.47 and ± 0.2 (which reveals prominent regions of +ve values for the Laplacian) can be seen in the figures below (and can be obtained as rotatable images by clicking).
 Laplacian isosurface contoured at ± 0.49 |
–
 Laplacian isosurface contoured at ± 0.47. Red = -ve, blue= +ve. |
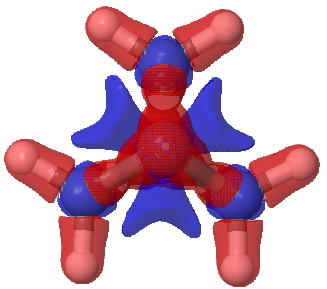 Laplacian isosurface contoured at ± 0.20 |
A significant feature is the isosurface at -0.47, which corresponds to the lowest contiguous Laplacian isovalued pathway connecting the two terminal carbon atoms (and which coincidentally is similar in magnitude to that reported5 as measured for these two atoms). Three such bent pathways of course connect the two carbon atoms. The energy density H(r) shows a minimum value of -0.21 au along any of these pathways. It is significantly less negative (-0.13) for the direct pathway taken along the axis of the C-C bond.
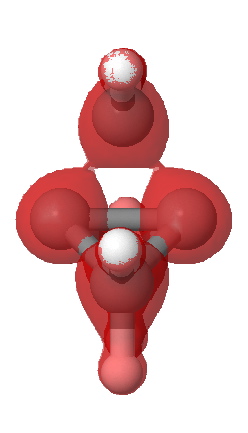 Energy density H(r) @-0.21 |
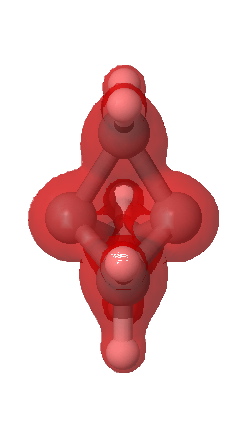 Energy density H(r) @-0.13 |
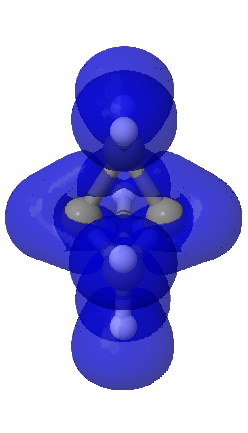 ELF isosurface @0.7 |
A useful comparison with this result is the ELF isosurface. This too is computed at the correlated CCSD/aug-cc-pVTZ using a new procedure recently described by Silvi.7 Contoured at an isosurface of +0.7, the ELF function is continuous between the two terminal atoms, much in the manner of Laplacian. Significantly, the ELF function at the bcp appears at the very much lower threshold value of 0.54, and forms a basin with a tiny integration for the electrons (0.1e). Since both methods provide a measure of the Pauli repulsions via the excess kinetic energy, the similarity of the Laplacian to the ELF function is probably not coincidental.
The issue then is whether a bond must be defined by the characteristics of the electron density distribution along the axis connecting that bond, or whether other, non-least-distance pathways can also be considered as being part of the bond.8 The former criterion defines a pathway involving a positive Laplacian (+0.095) and would be interpreted as indicating charge shift character for that bond. The latter involves three (longer) pathways for which the Laplacian is strongly -ve, and which would therefore per se imply more conventional covalent character for the interaction. Considered as a linear (straight) bond, it has charge shifted character; considered as three “banana” bonds, it may be covalent. Weird!
- Shaik, S.; Danovich, D.; Silvi, B.; Lauvergnat, D. L.; Hiberty, P. C., “Charge-Shift Bonding – A Class of Electron-Pair Bonds That
Emerges from Valence Bond Theory and Is Supported by the Electron Localization Function Approach,” Chem. Eur. J., 2005,
11, 6358-6371, DOI: 10.1002/chem.200500265 and references cited therein. - W. Wu, J. Gu, J. Song, S. Shaik, and P. C. Hiberty, “The Inverted Bond in [1.1.1]Propellane is a Charge-Shift Bond,” Angew. Chem. Int. Ed., 2008,
DOI: 10.1002/anie.200804965; 10.1002/cphc.200900633 - S. Shaik, D. Danovich, W. Wu & P. C. Hiberty, “Charge-shift bonding and its manifestations in chemistry”, Nature Chem, 2009, 1, 443-3439. DOI: 10.1038/nchem.327
- P. Coppens, “Charge Densities Come of Age”, Angew. Chemie Int. Ed., 2005, 44, 6810-6811. DOI: 10.1002/anie.200501734
- M. Messerschmidt, S. Scheins, L. Grubert, M. Pätzel, G. Szeimies, C. Paulmann, P. Luger. “Electron Density and Bonding at Inverted Carbon Atoms: An Experimental Study of a [1.1.1]Propellane Derivative, Angew. Chemie Int. Ed., 2005, 44, 3925-3928. DOI: 10.1002/anie.200500169
- L. Zhang, W. Wu, P. C. Hiberty, S. Shaik, “Topology of Electron Charge Density for Chemical Bonds from Valence Bond Theory: A Probe of Bonding Types”, Chem. Euro. J., 2009, 15, 2979-2989. DOI: 10.1002/chem.200802134
- F. Feixas , E. Matito, M. Duran, M. Solà and B. Silvi, submitted for publication. See also this abstract.
- See for example the work of R. F. Nalewajski
Rzepa, Henry S. The weirdest bond of all? Laplacian isosurfaces for [1.1.1]Propellane. 2010-07-21. URL:http://www.ch.ic.ac.uk/rzepa/blog/?p=2251. Accessed: 2010-07-21. (Archived by WebCite® at http://www.webcitation.org/5rOFp6EuM)
Tags: electronic energy, energy, energy density, excess kinetic energy, Hiberty and co, Hypervalency, Interesting chemistry, kinetic energy density, potential energy density, representative, X-ray
[…] between experiment and quantum mechanics, and their usefulness has been noted in this blog on previous occasions. However, note that in this designed structure, the O…C distances are merely 2.65-2.7Å, […]
[…] The Laplacian has a positive value at this point, possibly an indication a charge-shift bond (see this and this blog, although more likely due to the adjacency of the bond critical point to the core […]
[…] This molecule is however normally represented with bonds only to the peripheral carbons, and with no bond to what is after all the shortest of the four […]
[…] For example, it might in fact be an anomalous result since the H…H region may in fact have charge-shift character,[3] which can change the characteristics of the density Hessian (and its […]