

Next: 3.4 Atomic charges
Up: 3. Topological analysis of the electron
Previous: 3.2 Gradient field analysis
Further analysing the first and second derivatives at the critical points
validate the assumption of ionic bonding in the silatrane.
Table 5:
Properties of the critical points in the chiral silatrane
| Si(1) O(2) |
bcp (3,-1) |
|
|
|
coordinates |
X = 4.24113875 Å |
Y = -1.48450393 Å |
Z = -0.45686378 Å |
|
distance from |
Si 1.27 Å |
O 1.87 Å |
|
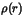 |
0.1203 e/a03 |
|
|
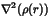 |
0.964 e/a05 |
|
|
| Si(1) N(5) |
bcp (3,-1) |
|
|
|
coordinates |
X = 3.15303269 Å |
Y = -0.135561143 Å |
Z = 0.158368394 Å |
|
distance from |
Si 1.56 |
N 2.54 |
|
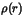 |
0.0497 |
|
|
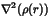 |
0.148 |
|
|
The low electron density at the critical points and the positive Laplacian
(
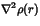 )
are clear evidence that the bonds are more ionic than
covalent. As one compares these results to those obtained by Gordon
[12] there is a good agreement with results obtained on 6-31G(d)
optimised structures, showing that the X-ray structure is a valid geometry for
doing ab-initio calculations.
)
are clear evidence that the bonds are more ionic than
covalent. As one compares these results to those obtained by Gordon
[12] there is a good agreement with results obtained on 6-31G(d)
optimised structures, showing that the X-ray structure is a valid geometry for
doing ab-initio calculations.
To connect the analysis to the concept of the bond order (which is more familiar to the
preparative chemist),
Bader has derived an expression to calculate the bond order n
from the electron density 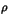 at the bond critical point
[16]:
at the bond critical point
[16]:
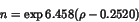 |
(1) |
Comparing the bond orders derived by Mulliken population analysis and
calculated using equation (1) one finds that the silicon-oxygen bond is
attributed a much more ionic character in the Bader analysis (table 6).
Table 6:
Bond Order
| bond |
Mulliken derived |
Bader |
| Si(1)-O(2) |
0.897 |
0.427 |
| Si(1)-N(5) |
0.237 |
0.270 |


Next: 3.4 Atomic charges
Up: 3. Topological analysis of the electron
Previous: 3.2 Gradient field analysis
Bjoern Pedersen
1998-06-18