Studies of Imidazole and Pyrazole Protonation using Electrostatically Trained Neural Networks

Howard B. Broughton, Stuart M. Green and Henry S. Rzepa

Neuroscience Research Centre, Merck Sharp and Dohme, Terlings Park, Harlow, Essex CM20 2QR

Department of Chemistry, Imperial College, London SW7 2AY

To whom all correspondence should be addressed. Current address: Center for Molecular Design, Campus Box 1099, Washington University, St. Louis, MO 63130-4899. Email: stuart@wucmd.wustl.edu

Introduction

Neural networks are now finding regular application to a variety of chemical problems: spectroscopy[2][1], prediction of protein structure[6][5][4][3] and water binding sites[7], synthetic analysis[10][9][8], solvation studies[11]. This rapidly growing field has already spawned two reviews, by Burns and Whitesides[12], and Gasteiger and Zupan[13]. The realm of quantitative structure-activity relationships (QSAR) has seen a great deal application of such neural paradigms[18][17][16][15][14] as they make an obvious alternative to the multivariate statistics traditionally used in Hansch analysis.

In preliminary studies we successfully trained a neural network with a series of imidazole MEPs (AM1 derived) in attempt to predict histidine p perturbation in triosephosphate isomerase[19]. Such a regime uses the neural network to derive a three-dimensional quantitative structure-activity relationship (3D-QSAR) - inputs to the network are sourced directly from grid points of the MEP (freeing us from the restrictions imposed by substituent parameters). The network is then trained to map these points to the molecular property (p). Statistical techiniques such as comparative molecular field analysis (CoMFA[20]) have also been developed to perform 3D-QSAR, but these methods presuppose some form of non-parametric[21] or more restrictive parametric[20] relationship between individual field points and the observable quantity. Neural networks offer an alternative where no assumption is made about the relationship between property and field; instead this is derived during the process of training the network.

To test the 3D-QSAR abilities of the neural network further, this paper details the results of using different basis sets or Hamiltonians for deriving the MEP in the imidazole p case. The results of training pyrazole p and/or proton affinity (PA) against MNDO MEPs are also discussed.

Computational Methods

All structures were optimised using either MOPAC[22] or Gaussian[23] for the respective semiempirical method (AM1, PM3 and MNDO, using EF and PRECISE) or basis set (STO-3G, 3-21G and 6-31G*). Each optimised molecule was then aligned such that atom 1 (Figure 1 and Figure 3) was placed at the origin, with atom 2 extending out along the positive X-axis and atom-3 in the XY-plane. Where atoms 1, 2 and 3 are consistently defined for all. The MEP was then evaluated, with each respective method, on a 1.5 Å grid excluding points that were within the van der Waals radii and those which were more than 6 Å from the closest atom.

For suitable input to the neural network only grid points common to all molecules in either imidazole or pyrazole set were used. Each MEP point was then scaled such that the value presented to the network lay in the range 0.1 to 0.9 (in order to prevent network saturation).

Where 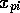is the scaled input for molecule 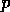at grid location 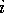, 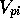is the MEP value, 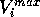and 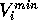are the respective maxima and minima for all molecules at the MEP point 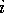. The p values to which the inputs would be trained against were also similarly normalised.

The neural network used in this study was of the backpropagation type[26][25] with one hidden layer of 10 neurons and a final layer with a one neuron, for single property prediction, or two, when combined properties are used. All neurons had a sigmoidal activation function and a single bias term (fixed input of 1.0). Initially, all neuronal weights were randomly set (uniform distribution) to values between 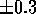. The scaled MEPs were trained to map to their respective properties in `batch mode', ie. all patterns were presented and the network updated with the sum of errors. Network updates were performed using a fast adaptive learning algorithm (superSAB[27]). This method was found to be much stabler and require far less iterations to achieve the required degree of training than the traditional generalised delta rule[25].

Due to the initial random weights the network cannot be guaranteed to produce the same results for every random seed, hence many differently seeded trainings were used for each crossvalidation step with all predictions included in the subsequent analysis.

Results and Discussion

A. Imidazole p QSAR with MEPs.

A collection of small, conformationally invariant imidazoles of varied substitution were selected (Table 1), these covered a range of 10 p units. The geometry of each of these 26 imidazoles was optimised and MEPs calculated for all methods described. A leave-one-out crossvalidation analysis was then performed for all 26 imidazoles training five differently seeded networks to map MEP to p for 25 of the imidazoles, then predicting the p of the excluded imidazole (Figure 2).

Two molecules (5NO-1Me and 5F-1Me) are expressed as outliers independent of the MEP derivation methods, this is due to the lack of 5-substituted moieties and the network is relatively uneducated about these types of species. With the semiempirical methods and STO-3G the common outliers are all molecules containing chlorine suggesting a poor electrostatic description of chlorine by these methods due to an incorrect definition of the atomic core[28].

Overall,

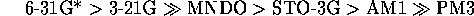
the best performing networks were those trained with the high level ab initio derived MEPs, although there is little improvement (but considerable effort) in going form 3-21G to 6-31G*. The poor performance of PM3 is to be expected due to the poor parameterisation of nitrogen[29].

In previous comparisons of MEP derivation methods[31][30], workers have assumed those determined for the highest feasible level of theory were the most `realistic' and used this level as a standard. From this work with imidazoles one can suggest an order of how realistic the techniques are in producing MEPs by correlating them with real experimental data, rather than via comparison with a presumed standard.

B. Pyrazole p and PA QSAR with MEPs.

Neural networks were also trained to map the MEP to the p and PA of a series of pyrazoles. Recent experimental (fourier transform ion cyclotron resonance spectroscopy) and theoretical (6-31G geometries and energies) work has demonstrated that for the tautomerism of NH pyrazoles (Figure 3) the equilibrium constant 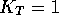[32] ie. 3- and 5-substituted moieties are inseparable, hence their p's and PAs are identical and both tautomers should be considered equally.

Proton affinity data[32] for 39 pyrazoles was used, 10 of these had equivalent tautomers, so a total of 49 pyrazoles were considered. The geometries of these were optimised and the MEP evaluated as before for the imidazoles but only at the MNDO level. A complete leave-one-out crossvalidation study for each pyrazole was carried out for five differently seeded networks. The results of this study are shown in Figure 4(a). A much larger dataset of 58 pyrazole p's was available[33], of these 33 had equivalent tautomers making an overall set of 91 pyrazoles. Exactly the same approach was used as in the proton affinity study, results in Figure 4(b).

Training is not restricted to the mapping of only one property at a time, any number of outputs can be included and the network trained to predict many things at once. Of the pyrazoles considered 21 are coincident between the p and proton affinity sets. Thus, these were used in a crossvalidation study but with training based on two outputs. For comparison purposes PA and p were also trained independently for the 21 pyrazoles. The results of this combined training (Table 5) are rather poor, the crossvalidations are nowhere near as good for those observed previously. This is not a failure of the network to cope with two outputs but just due to a lack of training data. Independent trainings on just the 21 pyrazoles against proton affinity or p yield almost identical results, hence the training of multiple properties is not detrimental to predictive performance.

Conclusion

We have demonstrated the utility of neural networks in the correlation of complex quantum mechanically defined features (MEPs) with experimentally determined parameter(s) for a given molecular series. The neural network, far from being the blind pattern classification method, shows the ability to generalise as it remains sensitive to the relative level of theory. Further studies based on trainings using alternative grid-based molecular descriptors and other properties (eg. biological activities) will hopefully expand this technique fully within the realm of 3D-QSAR.

Acknowledgment

We thank Merck Sharp and Dohme Research Laboratories and the SERC for financial support (to S.M.G.).

Footnote

Alternative grid definitions and numbers of neurons in hidden layer have been tested but this prescription was found to be best in a trade-off between performance and computation time[24]

References

1

B. Curry and D. E. Rumelhart. Tetrahedron Computer Methodology, 1990, 3, 213.

2

R. J. Fessenden and L. Gyorgyi. J. Chem. Soc., Perkin Trans. 2, 1991, page 1755.

3

N. Qian and T. J. Sejnowski. J. Mol. Biol., 1988, 202, 865.

4

M. J. McGregor, T. P. Flores, and M. J. E. Sternberg. Protein Eng., 1989, 2, 521.

5

D. G. Kneller, F. E. Cohen, and R. Langridge. J. Mol. Biol., 1990, 214, 171.

6

B. A. Metfessel, P. N. Saurugger, D. P. Connelly, and S. S. Rich. Protein Sci., 1993, 2, 1171.

7

R. C. Wade, H. Bohr, and P. G. Wolynes. J. Am. Chem. Soc., 1992, 114, 8284.

8

V. Simon, J. Gasteiger, and J. Zupan. J. Am. Chem. Soc., 1993, 115, 9148.

9

H. H. Luce and R. Govind. Tetrahedron Computer Methodology, 1990, 3, 143.

10

D. W. Elrod, G. M. Maggiora, and R. G. Trenary. Tetrahedron Computer Methodology, 1990, 3, 163.

11

N. Bodor, A. Harget, and M. Huang. J. Am. Chem. Soc., 1991, 113, 9480.

12

J. A. Burns and G. M. Whitesides. Chem. Rev, 1993, 93, 2583.

13

J. Gasteiger and J. Zupan. Angew. Chem. Int. Ed. Engl., 1993, 32, 503.

14

T. Aoyama, Y. Suzuki, and H. Ichikawa. J. Med. Chem., 1990, 33, 2583.

15

T. A. Andrea and H. Kalayeh. J. Med. Chem., 1991, 34, 2824.

16

S. S. So and W. G. Richards. J. Med. Chem., 1992, 35, 3201.

17

J. H. Wikel and E. R. Dow. Bioorg. Med. Chem. Lett., 1993, 3, 645.

18

Ajay. J. Med. Chem, 1993, 36, 3565.

19

H. B. Broughton, S. M. Green, and H. S. Rzepa. J. Chem. Soc., Chem. Commun., 1992, page 1178.

20

R. D. Cramer III, D. E. Patterson, and J. D. Bunce. J. Am. Chem. Soc., 1988, 110, 5959.

21

H. B. Broughton, S. M. Green, and H. S. Rzepa. J. Chem. Soc., Chem. Commun., 1992, page 37.

22

J. J. P. Stewart. MOPAC version 6.0. Quantum Chemistry Program Exchange no. 455, local modifications for grid based MEP calculation by S. M. Green.

23

M. J. Frisch, G. W. Trucks, M. Head-Gordon, P. M. W. Gill, M. W. Wong, J. B. Foresman, B. G. Johnson, H. B. Schlegle, M. A. Robb, E. S. Replogle, R. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C. Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart, and J. A. Pople. Gaussian 92, Revision B. Gaussian, Inc., Pittsburgh PA, 1992.

24

S. M. Green. Development of Neural Networks of Structure-Activity Relationships. PhD thesis, University of London, 1993.

25

D. E. Rumelhart, G. E. Hinton, and R. J. Williams. Nature, 1986, 323, 533.

26

J. McClelland and D. Rumelhart. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. MIT press, Cambridge, MA, 1986.

27

T. Tollernaere. Neural Networks, 1990, 3, 561.

28

L. Bonati, U. Cosentino, E. Fraschini, G. Moro, and D. Pitea. J. Comp. Chem., 1992, 13, 842.

29

I. Juranic, H. S. Rzepa, and M. Yi. J. Chem. Soc., Perkin Trans. 2, 1990, page 877.

30

K. M. Merz Jr. J. Comp. Chem., 1992, 13, 749.

31

I. Alkorta, H. O. Villar, and G. A. Arteca. J. Comp. Chem., 1993, 14, 530.

32

J. L. M. Abboud, P. Cabildo, T. Cañada, J. Catálan, R. M. Claramunt, J. L.G de Paz, J. Elguero, H. Homan, R. Notario, C. Toiron, and G. I. Yranzo. J. Org. Chem., 1992, 57, 3938.

33

J. Elguero, E. Gonzalez, and R. Jacquier. Bull. Chim. Soc. Fr., 1968, 12, 5009.

34

M. R. Grimmett. In Comprehensive Heterocyclic Chemistry, volume 5, page 384. Pergamon Press, 1984.

 
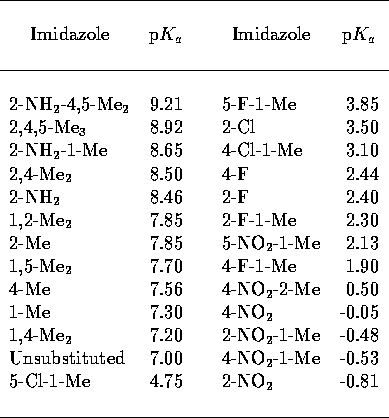
Table 1:   Substituted imidazole p[34]

 
Table 2: Crossvalidation statistics for mapping of MEP to p for 26 imidazoles. Each analysis based on all five different trainings.

 
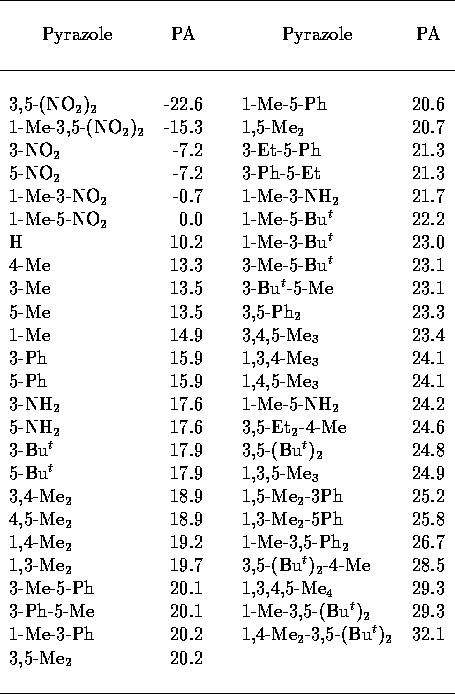
Table 3:   Experimental pyrazole PA[32].

 
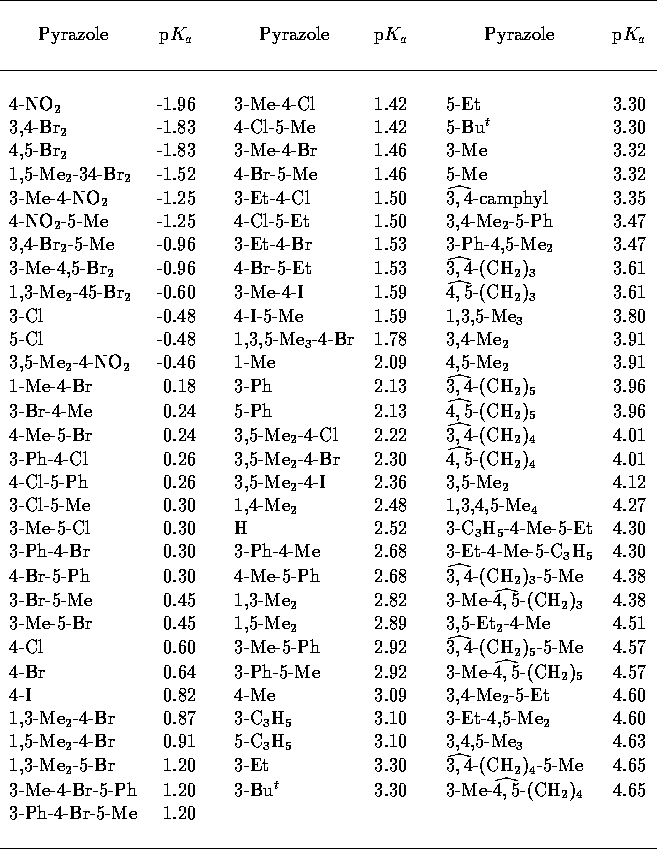
Table 4:   Experimental pyrazole p[33].

 
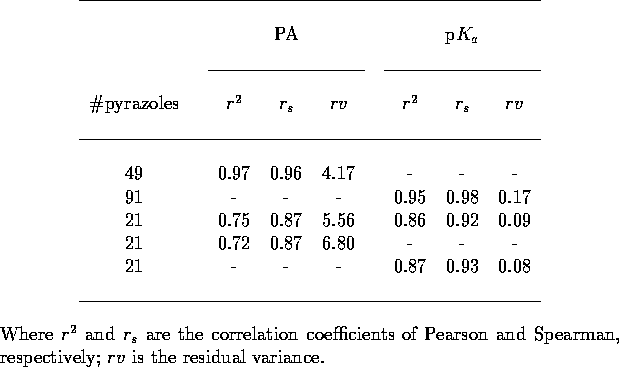
Table 5:   Crossvalidation statistics for pyrazole MEP training. All five different leave-one-out crossvalidations included in each analysis.

 
Figure 1:   Imidazole atom numbering.

 
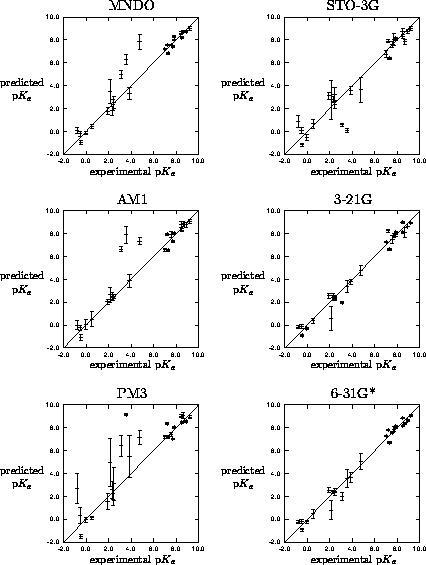
Figure 2:   Leave-one-out crossvalidation results for mapping of MEP to p for 26 imidazoles. Predicted p is mean of five independent trainings with error bar as the standard deviation.

 
Figure 3:   Pyrazole tautomerism and atom numbering.

 
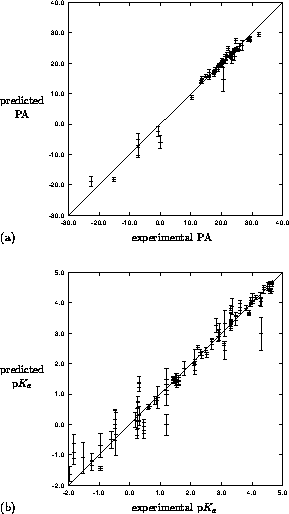
Figure 4:   Leave-one-out crossvalidation results for mapping of MEP to (a) PA for 49 pyrazoles and (b) p for 91 pyrazoles. Predicted property is mean of five independent trainings with error bar as the standard deviation.