 .
.
Up to now, a system with a finite number of hydrogen atoms
and a finite number of energy level
has been considered. In this section, a hydrogen chain/polymer
will be studied; the system is infinite, with an
infinite number of atoms and an infinite number of energy levels.
Since the chain is periodic, a cell with only a hydrogen atom
that is repeated by translation in one direction
is the way adopted to tackle this problem.
The cell is described by a lattice vector (or lattice parameter)
a.
The infinite number of electronic states, that form a continuum in
energy, are grouped together in a band.
The equivalent of the energy level diagram of a finite system
is the band structure.
Each level is labelled by a continuous variable k:
each value of k corresponds to an energy level.
The quantity k belongs to a space called,
the reciprocal space; in this space a cell
can be also defined, the reciprocal cell, and it is
useful and convenient, as the system is also periodic in
the reciprocal space.
The reciprocal lattice parameter a*
is related to the lattice parameter of the cell in direct space
according to the following formula:
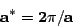 .
.
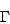 .
.
In this section you will calculate the wavefunction and the band structure(that is the energy level diagram for a infinite system) for the hydrogen polymer.
Exercise 1: Start DLVisualize, run a CRYSTAL calculation for the H polymer: H_polymer.inp
Exercise 2: Run a CRYSTAL properties calculation
of the band structure for the H polymer,
as explained in Exercise 3
for H4.
In other to visualize all the infinite energy levels it is
necessary to consider a path in the reciprocal cell
that has the same length of a*, for instance:
-a*/2 < k < a*/2
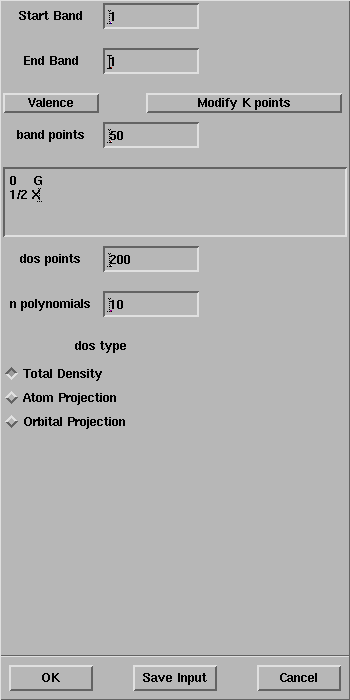
In the CRYSTAL Bands panel, type the coordinates of the
points
(note that the coordinates are expressed in unit of a*):
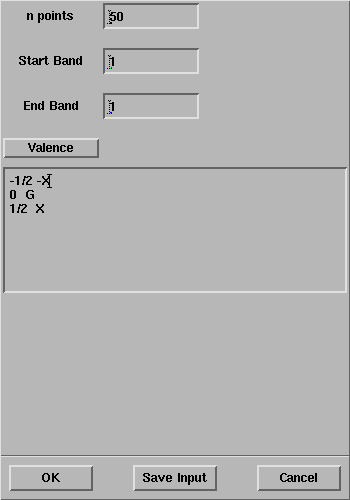
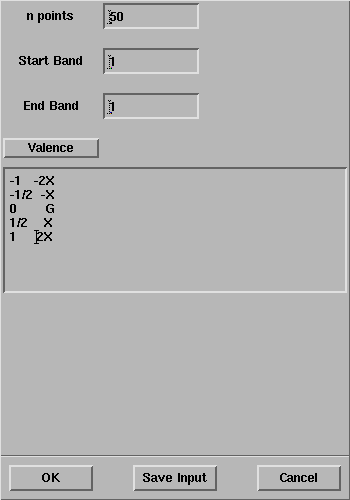
Compare the band structure obtained with a second band structure calculation,
with the path indicated below,
in order to show the periodicity in the reciprocal lattice:
However, the following path is generally adopted due to the symmetry
between k and -k:
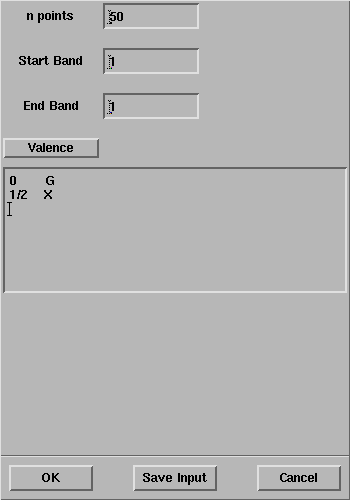
Exercise 3: Run a CRYSTAL properties calculation
of the density of states
for the H polymer,
as explained in Exercise 3
for H4.
Exercise 4: Run a CRYSTAL properties calculation
of the band structure + the density of states
for the H polymer,
as explained in Exercise 4
for H4.
In the CRYSTAL Bands + DOS panel,
select the following path: