In order to retain the characteristic features of quantum mechanical force fields, for example, a particular distribution of the signs of the off-diagonal elements and an approximate ratio between the force constants, a smaller number of adjusting parameters is used in the empirical correction than the number of parameters in the traditional solution of the inverse vibrational problem in which the role of the latter was played by the varying force constants themselves. Therefore, several procedures for scaling quantum mechanical force fields have been suggested.
Comparison analysis of different methods [4-9] of empirical scaling of quantum mechanical molecular force fields has been performed. The possibility of using each concrete scaling technique was shown to depend on the theoretical level of the quantum mechanical calculation [10]. Pulay's scaling method [8] (congruent transfomation of the force constant matrix, i.e.
Fs = D1/2 Fqm D1/2 (1)
where Fqm is the matrix of force constants, calculated, for example, in the Hartree-Fock approximation, and D is the diagonal matrix of the scaling factors) was found to be applicable when the relative accuracy of determination of both the diagonal and the off- diagonal quantum mechanical force constants is approximately equal. This constraint is fulfilled for the quantum mechanical force field as determined quite close to the Hartee-Fock limit [10, 11]. This makes it possible to carry out its correction with maximal retention of peculiarities inherent in the molecule under investigation [12-14].
Solution of the inverse vibrational problem on the basis of a quantum mechanical force field may be considered as a limiting case of scaling procedure where the maximal number of scale factors was used. However, this approach does not maintain the distribution of signs and the approximate ratio of the absolute values of the quantum mechanical force constants.
This is true, in particular, for a "regularized force field" [15], since search for the solution, nearest to F in the euclidean norm, ensures [16] retention of the signs of the force constants and of the approximate ratio between their absolute values only in the ideal case, i.e., in the case where the desired matrix is close to Fqm. However, in practical calculations, the norm of the difference between these matrices is large, because the calculated frequencies deviate from the experimental values by 10-20% on the average. Therefore, substantial changes in the force matrix and, consequently, in the vibrational modes, may arise during the iteration procedure (see, for example, Ref. 15). Then the formal solution may be inconsistent with the physical requirements to the assignment of the vibration frequencies that follow from quantum mechanical calculation. The introduction of the corresponding limitations on the assignment into the functional (2) being minimized (see Ref. 15) is rather difficult, which dramatically restricts the possibilities of the regularization method.
Thus, in the Pulay method [8], the attention is concentrated on the manner in which the correction of the quantum mechanical force field Fqm should be carried out with account for the physical requirements (retention of the modes of normal vibrations, i.e., the distribution of signs and the ratio of the force constants), whereas in the regularization method [15], the attention is focused on how much Fqm should be minimally modified from the viewpoint of the matrix norm, in order to achieve the best fit with the experiment. In the former case, qualitative agreement with Fqm is attained (the vibrational modes are retained), while in the latter case, the formal quantitative agreement, corresponding to the least deviation of the resulting matrix Fr from the initial matrix Fqm in the matrix norm, is obtained.

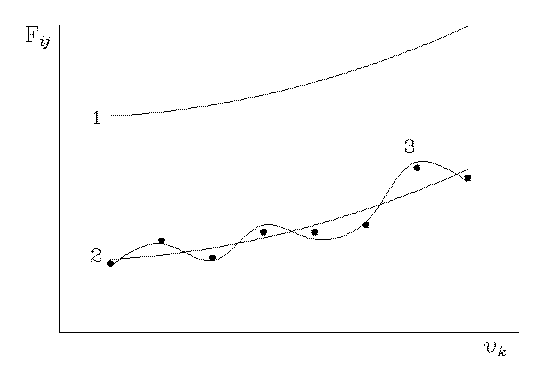
Fig. 1
This situation can be illustrated by Fig. 1 in which curve 1 conventionally describes the initial quantum mechanical force field Fqm, and curves 2 and 3 describe the final force fields, i.e., the scaled field Fs (see Eq. (1) and Ref. 8) and the "regularized" field Fr [15], respectively. The points denote the experimental parameters (for example, the vibrational frequencies) that have been used for the correction of the force field Fqm. The correction of curve 1 is conventionally reduced to its displacement and a variation of its form. When the scaling is carried out according to Pulay [8] using only one factor (homogeneous scaling), curve 1 is transformed unchanged into curve 2. In some cases this scaling makes it possible to assign even experimental vibrational frequencies of rotation isomers (see, for example, Ref. 17). If several similar scaling factors are used, curve 2 corresponds to a displaced and somewhat distorted curve 1, and the deviation of the calculated vibrational frequencies from the experimental values does not exceed the generally admissible limit. An example is provided by the correction of the quantum mechanical force fields of trans-1,3-butadiene [1], in which the scattering of the scaling factors for the force field in the MP2/6- 31G*// MP2/6- 31G* approximation was 0.07 (the minimum value was 0.88 and the maximum value was 0.95). It is clear that with the scaling factors being so similar, the ratios between the elements of a force matrix virtually do not change, and the vibrational modes for the frequencies calculated from Fs (see Eq. (1)), are retained almost completely.
In the case where the inverse vibrational problem is solved by the least-squares method or by the regularization method [15], when the disturbance of the distribution of signs of the off-diagonal elements and of the ratio between the diagonal and off-diagonal elements of the final force matrix Fr with respect to the initial matrix Fqm in the practical calculations is admissible, curve 1 is transformed into a type 3 curve. This is caused by the fact that in the regularization method, the minimum condition
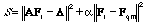 (2)
(2)
is used (A is a nonlinear operator that assigns a set of computable Λ values to each matrix of force constants Fr and α is an additional varying parameter, which is selected by a special procedure), with the calculated vibration frequencies being 10-20 % higher than the experimental values. Indeed, this leads to an inevitable considerable decrease in the diagonal force constants and to the compensation of this decrease by a variation of the absolute values and the signs of the off-diagonal elements of the force matrix. The resulting agreement of the calculated vibrational frequencies with their experimental analogs, due to the large number of fitting parameters, must be better than that in the case of curve 2. However, the significant properties of the ab initio force matrix that correspond to curve 1 are lost. The latter indicates that the setting of the problem in the regularization method is obviously incorrect from the viewpoint of the molecular vibration physics.
2. C. Møller and M. S. Plesset, Phys. Rev., 46 (1934) 618.
3. T. Ziegler, Chem. Rev., 1991, 91, 651.
4. P. Pulay, W. Meyer, J. Mol. Spectrosc., 40 (1971) 59.
5. W. Bleicher, P. Botschwina, Mol. Phys., 30 (1975) 1029.
6. C. E. Blom, C. Altona, Mol. Phys., 31 (1976) 1377.
7. K. W. Hipps, R. D. Poshusta, J. Phys. Chem., 86 (1982) 4112.
8. G. Fogarasi, P. Pulay, Annu. Rev. Phys. Chem., 35 (1984) 191.
9. J. Florián, B. G. Johnson, J. Phys. Chem., 98 (1994) 3681.
10. Yu. N. Panchenko, Rus. Chem. Bull., 45 (1996) in press.
11. V. I. Pupyshev, Yu. N. Panchenko, Ch. W. Bock, G. Pongor, J. Chem. Phys., 94 (1991) 1247.
12. Yu. N. Panchenko, N. F. Stepanov, Rus. J. Phys. Chem., 69 (1995) 535.
13. Yu. N. Panchenko, G. R. De Maré, N. F. Stepanov, J. Mol. Struct., 348 (1995) 413.
14. Yu. N. Panchenko, G. R. De Maré, V. I. Pupyshev, J. Phys. Chem., 99 (1995) 17544.
15. G. M. Kuramshina, F. Weinhold, I. V. Kochikov, A. G. Yagola, Yu. A. Pentin, J. Chem. Phys., 100 (1994) 1414.
16. T. Kato, Perturbation Theory for Linear Operators, Springer Verlag, Berlin, Heidelberg, New York, 1966.
17. Ch. W. Bock, Yu. N. Panchenko, and S. V. Krasnoshchiokov, Chem.Phys., 125 (1988) 63.