Möbius and Hückel Molecular Orbitals arising from C=C=C components in Annulene rings

Sonsoles Martín-Santamaría and Henry S. Rzepa*

Department of Chemistry, Imperial College of Science, Technology and Medicine, London, SW7 2AY, UK

Summary: Following our previous suggestion that C=C=C units can induce Möbius characteristics in cyclic annulenes, we present a more detailed analysis of the molecular orbitals generated by the interaction of such units with the p orbitals the annulene. For cycloheptatetraene (1) these take the form of two occupied Huckel orbitals with b symmetry, two occupied Möbius orbitals with a symmetry which can be sub-classified as having catenane or rotaxane forms, together with a more ambiguous p-like orbital generated from the s system. These latter C-H interactions can be reduced by studying instead the perfluorinated analogues. Computed NICS values revealed a diatropic (aromatic) ring current for perfluorocycloheptetraene. A series comprising cyclic (C=C=C)_n, n=1-4 in which the phase inversions are co-operative revealed that for n=1,3 the rings were aromatic, but anti-aromatic for n=2,4, resulting in a generalisation that 4n+2 occupancy of Möbius orbitals is required for aromaticity. An isomer of n=2 (6) in which the chirality of the C=C=C units is opposed revealed aromatic behaviour, which is discussed in relation to two other isomers 4 (p-benzyne) and 5 (bicyclo-octatriene). For n=4 a symmetry lowering Jahn-Teller-like distortion occurs, we think in analogous fashion to that observed for singlet cyclobutadiene. Further work is required to generalise the aromaticity of these Mobius-like molecules.

Heilbronner proposed¹ in 1964 that applying a Möbius-like phase inversion to systems containing 4n p electrons in a cyclically conjugated array could result in a novel form of aromatic molecule. His suggestion that this might occur with conformationally flexible annulenes has recently been confirmed with the identification of several Möbius-like conformations of [16]-annulene, for which Nucleus Independent Chemical Shift (NICS) calculations have indicated mildly aromatic behaviour.² Schleyer and co-workers³ have identified charged annulenes such as C₉H₉⁺ as exhibiting much more strongly aromatic Möbius behaviour. More recently we proposed⁴ that replacing a C=C bond in an annulene with C₂-symmetry creating fragment such as C=C=C might induce Möbius aromaticity. We cited cycloheptatetraene (1, R=H) and systems containing two C=C=C components of which cyclohexatetraene (2, R=H) is an example.

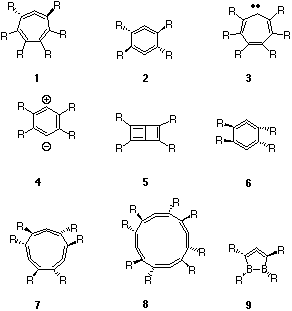
Both 1 and 2 can have planar 4n+2 p-aromatic valence bond isomers 3 and 4 (p-benzyne)⁵ respectively, although these may not be stable minima but can also be transition states for chiral inversion. Here we present an analysis of the key features of the Möbius annulenes in terms of p-molecular orbital correlation between the planar Hückel (H) aromatic stationary point and the twisted C₂ symmetric Möbius (M) system. We recognise that the s framework also has Möbius features, but do not deal with those in the present article.

Computational Procedure

Initial calculations were performed using the Chem3D (V 5.0) implementation of the AM1 semi-empirical SCF-MO method. Ab initio calculations at the restricted B3LYP/6-31G(d) level used G98W⁶ and the Chem3D interface to visualize the 3D form of the molecular orbitals. In general the form of the calculated AM1 and B3LYP/6-31G(d) orbitals was very similar, although minor variations in the relative ordering of the occupied orbitals were found, as noted in the text. The orbitals were correlated on the basis of the irreducible representations and visual inspection, there being no ambiguities observed on this basis. The 3D rendered orbitals were contoured at 0.01 a.u, saved in 3DMF format, and compressed for display. To view these orbital models via the supplemental information version of this article, a 3DMF viewer such as the Quick3D browser plugin or 3DMF Optimizer is required, together with QuickDraw3D libraries.

Results and Discussion.

1. Conversion of 3 to 1 (R=H).

An active orbital space including the first four virtual orbitals and seven occupied closed shell restricted orbitals to include the p-nodeless Hückel (H) orbital for 3 was selected for analysis and display (Figure 1), including two orbitals derived from the C-H bonds (6b, 7a for 1; 5b2, 7a1 for 3) for completeness but which we feel play no significant role in the analysis. Whilst planar species such as 3 and 4 will have significant biradical multiconfigurational character, use of the closed shell restricted orbitals are sufficient to establish the p/s origin of the orbitals in the Möbius form. Singlet state energies of all stationary points are given in Table 1.

Table 1. Calculated Energies for 1-9.

System	AM1 (kcal/mol)	B3LYP/6-31G*,Hartree	NICS(0),ppm
1, R=H	95.7	-270.2424	-5.7
3, R=H	117.0^a	-270.2079	-7.3
1, R=F	-156.1	-865.6199	-13.2
3, R=F	-135.3^b	-865.6075	-11.6
2, R=H	191.5	-230.7879^d	+22.2
2, R=t-Bu	114.2	-	-
4, R=H	167.6	-230.8479	-30.8
4, R=t-Bu	122.7	-	-
2, R=F	13.6	-627.7173	+23.3
4, R=F	13.7^c	-627.6986^e	+4.0
5, R=t-Bu	120.9	-	-
5, R=F	18.7	-627.7596	-24.8
6, R=F	10.4	-627.7404	-13.3
7, R=F	-82.7	-941.7215	-9.9
8, R=F	-125.5	-1255.6534 (-1255.6426)^f	(+2.1)
9, R=F	-143.4	-563.3521	-14.4
^a Transition state, with one imaginary normal mode; 301.5i cm^-1. ^b Transition state, with one imaginary normal mode; 274.6i cm^-1. ^c Transition state, with one imaginary normal mode; 1093.7i cm^-1. ^d AM1 geometry for 2. ^e. AM1 geometry for 4. ^f For D₂ syummetry. Value for D₄ symmetry in parentheses.

The symmetric 1b1 p-orbital of 3 correlates with 5b from 1, the latter being best described as a perturbed H-type orbital. Similarly the 2b1 p-orbital correlates with the H-type orbital 8b. The third occupied 1a2 p-orbital (corresponding to what would be a degenerate partner of 2b1 in e.g. benzene) correlates with the C₂ symmetric 8a orbital in 1, and this latter orbital is a clear example of a true Möbius (M) orbital, having no node in the plane of the molecule and hence presenting a single p-face for the system. The original carbene-like orbital in 3 (8a1) similarly transforms to a C₂ symmetric 9a M-type orbital in 1. Both 8a and 9a can be regarded as the key orbitals which impart p-Möbius characteristics to the system. One unusual aspect of these orbitals is their nodal properties. The 9a orbital has one phase forming two rings in a twisted figure eight shape, the other phase passing continuously through the each of the two rings (this can be seen more clearly when the orbitals are contoured at a lower level). The lower energy orbital 8a has one phase forming a twisted S shape, with the other phase passing through each of the two arcs. Heilbronner¹ noted that a formal HMO solution of the secular equations including a distributed Möbius overlap (resonance integral) results in a degenerate HOMO. Although the C₂ symmetric 8a and 9a differ by 1.6 eV (AM1) in energy, at least part of their energy separation is due to interactions with the s framework, not considered in the Heilbronner argument. More significant are the chiral properties of these two Möbius orbitals. Thus the direction of "twist" of 8a superimposed on the chirality defined by the nuclear positions is the opposite of 9a. Such chiral properties may well be a unique and characteristic feature of such pairs of Möbius orbitals.

The one remaining occupied p-orbital correlation is more ambiguous. A simple analysis indicates that three p-Hückel and one carbene-like s orbital in 3 should correlate with four occupied p-Hückel and p-Möbius orbitals in 1. However, the physical form of 7b suggests that it resembles the nodeless p orbital 5b, but differs in having two s-plane nodes along the C-H bonds. For orbitals such as this one, the s/p distinction may be difficult to make. Overall, 1 can be regarded as either a 2H + 2M, or as a 3H + 2M system if the 7b is regarded as having substantive p character. The computed NICS(0) value (B3LYP/6-31G*) for 1 is -5.7 ppm, indicating it to have only modestly diatropic ring currents compared with e.g. benzene (-9 ppm including paratropic contributions of the s-bonds, or -21 ppm for the p-only contribution).

The virtual orbital correlations indicate that 10a and 11a are both Möbius, and 9b and 10b are Hückel, although the latter does appear to have features which indicate nodeless connectivity between the top and bottom surfaces of the molecular plane.

2. Conversion of 3 to 1 (R=F).

Because of the ambiguous nature of the 7b orbital in 1 (R=H), we decided to inspect the perfuorinated analogues (R=F), arguing that the lower energy of the C-F s bonds would reduce the interaction with the higher energy carbon p system. The resulting diagram (Figure 2) indeed shows a much clearer separation of the s and p interactions, the active p space being straightforwardly the four highest occupied and the four lowest virtual orbitals.

The two H-type orbitals in 1 (R=F) are 16b and 17b, and the two M-type orbitals are 17a and 18a. These are closer to energy degeneracy than was the case with R=H, due we think to the reduced mixing with the s system, 18a having clearly much less C-R character than did 9a (R=H). This orbital also appears to have some of the in-plane p-conjugation noted by Schleyer and co-workers for the trannulene series.⁷. The two M-type orbitals again have opposite chirality. Another descriptor ithat could be applied to the two M-type orbitals is that 18a has rotaxane features, whilst 17a has catenane features. The distinction between these two features appears at least in part to be determined by the nature of the C-R bonds. It is also noteworthy that the rotaxane can be considered as having one more node than the catenane.

The NICS value 1 (R=F) of -13.2 ppm indicates perfluorination significantly increases the overall NICS(0) value of both the Möbius and the planar Hückel aromatics. A dissection of the individual orbital contributions in 1 to identify the precise origins of this effect is clearly a future requirement. In particular it would be important to establish whether the effect is associated with the elimination of the psuedo p orbital (7b for R=H) or with the reduced energy gap between the top two occupied orbitals.

3. Systems with Two C=C=C units. Conversion of 4 to 2 (R=H).

We felt at this stage it would be useful to study a homologous series in which the number and character of Möbius orbitals could be varied in some systematic manner, selecting for this purpose a series of cyclic systems comprising only C=C=C units. Their incorporation into a ring can be accomplished with co-operative chirality (leading to a systems with a C₂ or higher order symmetry elements) or opposed (leading to system with lower symmetry or with a C_s plane of symmetry)⁴. Considering first the system with two C=C=C units (2), the co-operative mode results in two enantiomers; the stereochemistry of that chosen for orbital contouring of 2 being shown in the scheme above. Although 1 and 2 both have a symmetry element (C₂) and 8 p electrons in common, there are significant differences between the two systems. Whereas the singlet carbene valence isomer 3 is distinctly higher in energy than singlet 1 (at high levels of theory representing the transition state for inversion of chirality of 1), the 6p aromatic singlet 4 (R=H) is 23.9 kcal mol^-1 lower in energy than 2 at the AM1 level. At ab initio levels, 2 (R=H) appears not to be a minimum, and for the purposes of comparison, the orbitals were evaluated at the optimised AM1 geometry. For R=F, 2 is now 0.1 kcal mol^-1 lower than 4.

We also investigated the relative energies for the bulky substituent R=^tBu, arguing that steric repulsion between the two bulky groups would be minimised in 2 and hence might stabilise it. This isomer is indeed calculated (AM1) as 8.5 kcal mol^-1 lower than singlet 4. However, as a synthetic target, 2 is unlikely to be viable, since the triplet state is calculated to be lower in energy than any of the singlets.

The orbital correlation diagrams (Figure 3) show many similarities with 1/3. For AM1-derived 2, R=H, two H-type orbitals are identifiable as 2b3 and 4b2, two M-type orbitals 3b1 and 4a, and again an ambiguous orbital (3b3) which derives from the s framework but has distinct p features. The relative orbital energies for 1 and 2 are also similar.

The two non-degenerate Möbius orbitals 3b1 and 4a in 2 (R=H) have similar forms to those of 1, R=H. Strikingly, the Möbius LUMO (4b1) has the same nodal properties as the HOMO but has opposite chirality, which as noted above may be a characteristic feature of Möbius systems. An approximate analogy with conventional stereochemical notation is that 3b1 and 4b1 form chiral diastereoisomers with respect to the nuclear framework, one bonding, the other antibonding. Again, we note that the 3b1 and 4b1 orbitals resemble a catenane, whilst the 4a orbital resembles a rotaxane. Finally, we note that in group theoretical terms, the 3b1 orbital in 2 correlates with the 8a Möbius orbital in 1 when the common C₂ symmetry element is considered.

4. Conversion of 4 to 2 (R=F).

For 4, R=F (Figure 4), both AM1 and ab initio methods again predict identical orbital occupancies. As with 1 (R=F), the lower energy C-F orbitals no longer interact with the p system and the s/p ambiguous orbital (3b3 for 2, R=H) is removed. The energy separation of the two M-type orbitals for 2 is now significantly less than 1(0.5 eV). The B3LYP/6-31G* energy ordering of 6b1 and 7a is inverted from the AM1 values, but the energy differences are small. One consequence of this orbital occupancy is that the ground state of 2, R=F correlates not with the ground state but with the the doubly excited state of 4, R=F, the correlation being between the two pairs 7a/6ag and 5b1u/7b1. Instead, the ground state of 2, R=F correlates instead with the ground state of 5, R=F, in which the occupied carbene-like orbital is in-phase, and a direct C-C central bond is formed. Allowed conrotatory ring opening of 5 leads directly to 2.

Both 2, R=H and F are predicted to have strongly paratropic ring currents (Table), which contrasts with the diatropic characteristics for 1. The nodal properties, energies and energy separations of the two Möbius HOMO p-like orbitals in 2, R=F (6b1 and 7a) appear to be very similar to their the equivalents in 1, R=F (17a and 18a) The ring current corresponds to a single-electron exitation operator, which would be expected to originate predominantly in the two symmetry allowed HOMO-LUMO transitions arising from the 6b1 to 7b1 or the 7a to 8a excitation in 2. The other transitions, e.g. 7a to 7b1 are symmetry forbidden. In contrast, the active space of four Möbius orbitals of a symmetry in 1 would give rise to four possible allowed excitations. To establish whether this effect might contribute to the paratropic character of 2, we also computed the C₂ symmetric 1,3-difluoro substituted system. The NICS value for this was +20.3 ppm, similar to +22 - +23 for R=H or F. This suggests that another factor must be responsible for the differing behaviour of 1 and 2. The correlation of ground state 2 with doubly excited (and anti-aromatic) 4 may indicate that the nature of 2 is associated with the orbital occupancy and not the nodal characteristics of the Möbius orbitals. To ascertain whether ring current was associated specifically with the relative chirality and hence phases of the two C=C=C units, we next studied the isomer 6.

5. Conversion of 4 to 6 (R=F).

The alternative chiral form 6, R=F is calculated to be 3.1/14.5 (AM1/B3LYP-6-31G*) kcal mol^-1 more stable than 2, R=F. This isomer could not be located for R=H. Since the geometries of 6 and 4 are very similar, it is no surprise that this is also true of orbitals of these two species Figure 4). The only significant difference is the presence of only a single Möbius orbital (7ag) which forms from the 2b1g orbital of the carbenoid. Unlike 2, R=F, the 5b1u orbital of 4 undergoes no transformation to any Möbius form, and so 6 (R=F) can be regarding as having 2H+1M+s orbital occupancy. In this regard, the two chirally opposed C=C=C units form one new Möbius orbital whereas two chirally co-operative units result in two Möbius orbitals. The ring currents for 2 and 6 are respectively strongly paratropic and diatropic, confirming that the chirality of the C=C=C unit may be an essential feature in understanding the aromaticity of these systems. We also note in passing the romantic form of the 7bu orbital in 6, which we tentatively christen the valentine orbital.

6. Systems with (C=C=C)_n, n=1, 3, 4.

We decided next to identify the characteristic features of the homologous series comprising (C=C=C)_n units, where n=1-4. Rings comprising three (7) or four (8) C=C=C units are straightforward to construct. We have not attempted to explore all the possible isomers, restricting ourselves to D₃ and D₂ symmetry respectively. For n=1, we had to employ a subterfuge, since the 3-ring formal analogue could not be located. Instead, we inserted two R-B units to make a five membered ring, but of course without increasing the p-electron count (9).

Along the series n=1-4, equal numbers of occupied M- and H-like orbitals are formed (Figure 5). The computed NICS values (Table) indicate aromaticity for n=1 and 3, anti-aromaticity for n= 2, 4, although attenuating as the ring size increases. This in fact corresponds to a 4n+2 rule for aromaticity as applied to the total number of either Möbius OR Hückel orbitals! The single Möbius HOMO orbital for 9 and the doubly degenerate Möbius HOMO orbital for 7 also follow the pattern found for 2-electron and 6-electron Hückel aromatics. The anti-aromatic 2 and 8 may not have degenerate HOMO orbitals, possibly because, like cyclobutadiene, of a contribution from Jahn-Teller distortion. This latter conclusion is supported by the distortion of 8 from the expected D₄ symmetry to the lower energy D₂ form. Along this series at least then, one can conclude that electron counting rules must be applied individually to the Möbius and Hückel occupied orbitals, rather than jointly. Doing this, one arrives at a 4n+2 rule for aromaticity in this series. In effect, if each C=C=C unit is regarded as contributing one phase inversion, then aromaticity arises from an odd number of such inversions, and anti-aromaticity (or Jahn-Teller-like distorsion) from an even number.

Conclusions

The inclusion of one or more C=C=C units into a cyclic annulene can result in chiral molecules which have a two or higher-fold axis of symmetry and some measure of Möbius characteristics. For this series however, the simplistic 4n rule for p Möbius aromaticity needs to be augmented with a more detailed analysis of how the C=C=C unit interacts with other p systems in the ring. When ring C-H bonds are present the Möbius orbitals can interact significantly with the s framework, leading to a "ghost" p-like Hückel orbital, an effect which can be reduced by studying the C-F systems.

In system 1 which involves the interaction of a 4-p C=C=C unit with 4 p electrons in a diene unit, the result is a pair p occupied Möbius-like and a pair of Hückel-like orbitals. 4n Electron occupancy of the two lowest energy Möbius orbitals then gives rise to overall aromaticity. For the series of which 1 is a member, additivity of chirality of the C=C=C units results in a series where 4n+2 occupied Möbius orbitals results in aromaticity and 4n occupancy results in anti-aromaticity.

A further generalisation for how one or more C=C=C units interact with alkenes and alkynes in cyclic annulene-like systems is clearly a desirable future objective, along with an analysis of how higher order cummulenes (e.g C=C=C=C=C) can interact to produce Möbius-like molecules.

Acknowledgements: We thank P. v. R. Schleyer and M. Mauksch for stimulating discussions.

References

E. Heilbronner, Tetrahedron Lett., 1964, 29, 1923.
S. Martin-Santamaria, B. Lavan and H. S. Rzepa, Perkin Trans. 2, 2000, 1415. More than thirty annulene conformations ranging from C₉ to C₁₆ that display Möbius aromaticity are identified in M. Mauksch, Thesis, Erlangen 1999 (P. v. R. Schleyer and M. Mauksch,personal communications).
M. Mauksch, V. Gogonea, H. Jiao and P. v. R. Schleyer Angew. Chemie Int. Edition, 1998, 37, 2395. For references to the NICS technique, see H. Jiao and P. v. R. Schleyer, J. Phys. Org. Chem., 1998, 11, 655.
S. Martin-Santamaria, B. Lavan and H. S. Rzepa, ChemComm, 2000, 1089.
For reviews on the chemistry of and calculations on p-benzyne, see W. Sander, Acc. Chem Res., 1999, 32, 669; R. Lindh, A. Bernhardsson, M. Schutz, J. Phys. Chem A, 1999, 103, 9913; H. Kenttamaa, J. Chem. Soc, Perkin Trans 2,, 1999, 2233-2240.
Gaussian 98, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, , T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle, and J. A. Pople, Gaussian, Inc., Pittsburgh, PA, 1998.
A. A. Fokin, H. Jiao and H, P. v.R. Schleyer, J. Am. Chem. Soc., 1998, 120, 9364.

Figures

Figure 1. Orbital correlations (AM1) for conversion of 3 to 1 (R=H)
Figure 2. Orbital correlations (AM1, B3LYP/6-31G*) for conversion of 3 to 1 (R=F)
Figure 3. Orbital correlations (AM1) for the conversion of 4 to 2(R=H)
Figure 4. Orbital correlations (AM1, B3LYP/6-31G*) for conversion of 4 to 2 and 6 (R=F)
Figure 5. Hückel and Möbius p-Orbitals for 9, 2, 7 and 8