Abstract: A series of C2-symmetric homo-derivatives of the cyclo C9H9+ cation first identified by Schleyer as Möbius aromatic are shown to themselves sustain Möbius 4n-electron homoaromaticity. Analogous double-twist Möbius bis-homoaromatics follow a 4n+2 electron rule. AIM (Atoms-in-molecules) and ELF (Electron localization function) analysis of the electron topology in the region of the homo-bond of these systems reveals that the presence of a AIM bond-critical point in this region is not mandatory, it being unstable to subtle variations in the local electron density induced by local or remote substitutents, and which can in turn induce self-annihilation or creation of a pair of bond and ring critical points. The same substituent-induced annihilation/creation of such a BCP/RCP pair can also be observed in the non-classical norbornyl cation. We suggest that the ELF thresholds for any basin found in the homo-region are better indicators of the delocalized nature of the homo-aromatic interaction.
Homoaromaticity is a term introduced by Winstein1 in 1959 to describe systems in which the σ framework of a cyclic conjugated and planar aromatic (4n+2) π-electron framework is interrupted with one or more bridging CH2 groups. This results in through space rather than through bond overlap of the pπ-pπ framework. Since then a large body of work has concluded that the phenomenon manifests best in cationic systems, of which the homotropylium ion 1 is held as the archetypal example.2 Homoaromaticity as described by Winstein has thus far been exclusively interpreted in terms of benzenoid models in which the pπ-pπ overlaps occur with preservation of an (idealized) plane of symmetry; the so-called Hückel aromaticity model. Yet there is another model, an asymmetric (disymmetric) one characterized as having (idealized) axes of symmetry only, and which has become known as the 4n-electron Möbius aromaticity model3. This distinction was first clearly introduced as a convenient selection rule for the transition states of pericyclic reactions4 in 1966, but has been extended only over the last decade to a still relatively small number of characterized instances of Möbius aromatic systems5. The first (and still one of the best) examples to be identified is the C9H9+ cation, shown by Schleyer6 to be an 4n eight π-electron delocalized and chiral aromatic cycle 2 bearing a C2 axis of symmetry only. Here we report a theoretical exploration of the properties of what what we term Möbius homoaromaticity in systems derived from 2.
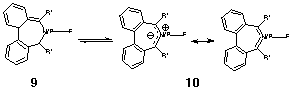
Combining the characteristics of 1 and 2 results in the C2-symmetric 8-π-electron 3 (X=CH2), in which the π system undergoes one half twist in the cycle. Any homoaromaticity would be defined by the degree of conjugation sustained across the C1-C9 bond in this species and whether any resulting ring current in the system is strongly diatropic. The latter is most simply quantified by the NICS index introduced by Schleyer.7 Preliminary results for the prototypic system 3, X=CH2 were reported elsewhere,8 B3LYP/6-31G(d,p) calculations indicating that the C1-C9 bond was surprisingly short (Web enhanced Table 1), but that this value was also associated with a low degree of bond length alternation (i.e. delocalization) in the ring defined by the sp2-hybrid carbon atoms. This alternation can be simply approximated by specifying the difference between the shortest and longest bonds in this cycle (Δr) and has the value of 0.035Å in this instance. If in fact the structure was better represented by the bicyclic isomer 4 (with a formal σ-single bond between C1-C9), the acyclic delocalization would only extend between C2-C8, and the C1-C2 bond would also be close to a single bond in length (it actually has a predicted value of 1.419Å, close to the typical aromatic value in benzene). This aspect can be tested further by calculating the anion of 3, X=CH2, which as a 4n+2 10-electron half-twist system would yield a Möbius homo-antiaromatic. The molecule avoids this (high energy) solution by instead adopting the anionic form of 4, for which the C1-C9 and C1-C2 bonds are indeed both long (1.502 and 1.480Å respectively, Δr 0.113A) and sustaining 8 acyclic rather than 10 cyclic conjugated π-electrons. Winstein has previously noted analogous behaviour for metallocomplexes of 1.9 Thus whilst 1 coordinated by Cr(CO)3 (a 6π-acceptor) is genuinely homoaromatic; when coordinated by Fe(CO)3 (a 4π-acceptor), the complex instead adopts the bicyclic form with a formal single bond between C1-C7.

To characterize the nature of the C1-C9 bond in 3 (X=CH2), we used Bader's critical point analysis10 of the electron density (AIM), and the related ELF11 (electron localization function). AIM (Atoms-in-molecules) involves analysis of the rate of curvature (Laplacian) of the electron density ρ(r) in terms of four types of so-called critical points, at each of which the derivative of ρ(r) is zero. These four are nuclear critical points (located at the nuclei), bond critical points (BCP) located between (normally pairs of) nuclei, ring critical points (RCP, defining a ring of nuclei) and cage critical points (CCPs). A topological relationship (the Poincaré-Hopf rule) between the numbers of each type of critical point states that NCP - BCP + RCP - CCP = 1. This method has previously12 been applied to 1, with the surprising result that no BCP can be identified in 1 along the path connecting C1 to C7. In recognition of this feature, 1 has become known as a no-bond homoaromatic species. It remains contentious whether the topological interpretation of the electron density provided by this analysis necessarily relates to the best chemical description of the bonding. In any event, 3 also exhibits no BCP in the C1-C9 region (Figure 1), although the predicted separation of these nuclei is in fact much shorter than that for 1 (Web-enhanced Table). The AIM analysis does however provide precisely one RCP for 3 (X=CH2) and its coordinates provide a convenient location for measuring the magnetic properties of this system via the NICS (nucleus independent chemical shift).7 Thus the NICS(rcp) of 3 has the value of -11.4 ppm (in comparison, benzene has a value at the equivalent ring centroid of ~ -10 ppm, and 1 has a value of -11.5 ppm). By these various measures, 3 (X=CH2) is clearly aromatic, and more specifically homoaromatic.

Figure 1. Critical points for (a) 3, X=CH2, (b) 3, X=CH2 CH2. The ρ(r) values (in e.Å-3, B3LYP/6-31G(d,p) ), at RCP points (yellow) 1 are 0.004, and 0.072 at point 2. In (b), the helicity of the system causes the RCP to split into two such points, connected by a CCP (green). Such behavior has been previously noted.13
It has recently been argued that a better chemical interpretation is provided not by the topology of electron density, but by a related measure known as the electron localization function (ELF(r)).14 As with AIM, critical points can be identified in the properties of this function, but in fact a more useful analysis is the localization domain reduction tree (LDRT), which is used to identify so-called basins in the ELF topology. An ELF(r) value of 1.0 represents perfectly localized electrons, achievable for no molecule. Approached from an ELF(r) value of < 1.0, the thresholds at which the ELF basin in the region of any putative bond first appears and then vanishes are useful indications of how localized the chemical bonding is. Thus the basins for most conventional bonds vanish to a point at ELF(r) values of ~0.94-0.95, whereas weaker interactions such as hydrogen bonds, agostic interactions or π-stacking may not even sustain the formation of discrete basins. The basins themselves can be two-centered (disynaptic) or three centered (trisynaptic). The disynaptic basin for the C1-C9 bond in 3, X=CH2 designated V(C1,C9), has a ELF(r) 0.675 for its bifurcation and 0.776 at its vanishing point (Web-enhanced Table 1). This relatively low value suggests that the C1-C9 "bond" is significantly less localized (more delocalized) than a conventional (single) bond type.
With these methodologies established for characterizing the species, we next explored the results of varying the nature of the bridging group X. For the larger bridge X=CH2-CH2, similar results were obtained in all but one regard. The C1-C9 bond length was slightly longer, Δr was somewhat larger, but the NICS(rcp) was still characteristic of an aromatic system. However, the system now did exhibit (Figure 1b) a BCP in the C1-C9 region, despite the nuclei being further apart! The V(C1,C9) value (0.879) also indicated somewhat more localized bonding, tending towards 4. One can conclude from this that the presence or absence of a BCP in the AIM analysis does not necessarily provide a fully chemical interpretation of the bonding.
Our task now became one of exploring whether chemical characteristics for predicting whether a BCP might be expected in any given bonding region can be defined. This was achieved by systematically varying the electron demand of X, via both the central atoms, and their substituents. Thus X=C(SiH3)2 increases the electron donation of the substituent, and the critical point analysis now changes quantitatively, in revealing two additional critical points compared to X=CH2, comprising one BCP and one RCP. It can be seen from the Poincaré-Hopf condition that creating one of each does not change the overall adherence to this rule. One can draw a (loose) analogy to the creation and subsequent annihilation of virtual pairs of nuclear particles. In our case, if the pair of BCP + RCP points is relatively close in space and in value of ρ(r), they will be prone to self-annihilate.13 Looked at in this manner, the presence (or absence) of a BCP+RCP pair is merely the consequence of subtle changes in the electron density in the region of the pair, and not a fundamental of the bonding of the molecule. Thus increasing the electron density in the C1-C9 region enables the creation of such a BCP+RCP pair, and it also increases the V(C1,C9) threshold. Conversely, removing electron density might be expected to encourage any geometrically close BCP+RCP pair to self-annihilate.
The remaining entries in the Table provide support for this hypothesis. Thus the electron releasing X=BH2 induces the creation of a BCP+RCP pair in the C1-C9 region, but BF2 reverses this effect (Figure 2b, c). When the central atom in X is B or Al, the overall charge on the system is zero (it being zwitterionic), and the NICS(rcp) and Δr values suggest even more highly homoaromatic molecules. Indeed, even the anionic X=BeH2 seems to sustain the effect.

Figure 2. Critical points for (a) 3, X=BH2, (b) 3, X=BF2. The ρ(r) values (in e.Å-3, B3LYP/6-31G(d,p) ), at RCP point (yellow) 1 and BCP point 2 (red) are 0.134 and 0.140 respectively. In (b), these two points have self-annihilated as a result of replacing H by F.
The ELF(r)C1-C9 basins also proved sensitive to substitution (Web-enhanced Table 1). If electron density is injected into this region, the vanishing threshold for the basin increases (towards that of a localized single bond). Conversely, electron withdrawal could inhibit even the formation of any basin in this region (e.g. X=SiF2, AlF2), and some basins have scarcely formed before they vanish at higher ELF values (X=BH2). These features suggest that analysis of ELF(r)C1-C9 values provides a more useful chemical interpretation than provided purely by the presence or absence of bond critical points in the AIM analysis.
The concept can also be extended to Möbius bis-homoaromaticity. The dication 5, X=CH2 comprises two 5π cationic components in which cyclic conjugation and hence aromaticity occurs across two CH2 bridges. Having D2-symmetry, it represents a double half-twist Möbius homoaromatic, for which a 4n+2 electron selection rule applies.15 The neutral 5, X=BH2 is even more (homo)aromatic, with a shorter homo bond length and a larger NICS(rcp) value.

The specific example of X=BeF2 gave the same number of BCPs as did X=CH2, but they occurred in different regions. Whereas no BCP was present along the C1-C9 region for X=CH2, two BCPs were located along C1-X and C9-X (Figure 1a). For X=BeF2, one a BCP is located in the C1-C9 region, and the second BCP lies along the path apparently connecting the first BCP to X (Figure 3a, point 1). This rather odd AIM-BCP behavior has in fact been computed16 in another cationic system, the norbornyl cation 6 (also famously associated with Winstein). Two representations of the symmetrical species (in which the group ZY2; Z=C+, Y=H bridges symetrically across the C1-C2 bond) have been argued over. Representation 6a is that of a π-complex, in which the pair of π-electrons in the C1-C2 alkene donate into the vacant p-orbital on Z. The other, 6b, is a non-classical two-electron-3-center interpretation, in which (weaker) bonding is considered as occurring between each of C1 and C2 and Z. In terms of the AIM critical point analysis, 6a results in a BCP along the C1-C2 path, and a second BCP occurs along the path connecting the first BCP and Z (Figure 3b).18 This is the result recovered for Z=C+, Y=H. From our experiences above, one might expect a different result to be obtained if ZY2 were to be made more electron releasing. Thus for the (neutral) system Z=B, Y=SiH3, just such is computed. An additional BCP + RCP pair is created, and BCPs now occur along C1-C2, C1-Z and C2-Z, and a RCP occurs at the centroid of this 3-membered ring, this effectively being representation 6b (Figure 3c). Thus these two representations are therefore really just small, but subtle variations in the electron density topology, which differ only in whether a BCP+RCP pair is created or annihilated. Because this creation/annihilation only occurs when the critical points are close (it is estimated < 0.2Å),13 this effect is only likely to be encountered for small, e.g. 3-membered rings; it no longer occurs for the larger 4-ring (3, X=CH2CH2).

Figure 3. Critical points for (a) 3, X=BeF2, (b) 6, Z=C,Y=H. (c) 6, Z=B,Y=SiH3. The ρ(r) values (in e.Å-3, B3LYP/6-31G(d,p) ), at BCP point 1 (red) are 0.050, 0.085 and 0.105 respectively and for RCP 2 (C), 0.105. Self-annihilation of points 1 and 2 in (c) results in point 1 in (b) remaining.
The hitherto unexplored concept of Möbius homoaromaticity emerges as a new addition to the many diverse types of molecule that are regarded as having aromatic character. The effect appears equally prominent in cationic, neutral and anionic molecules, and also appears to sustain higher-order half-twists in the Möbius topologies, corresponding to e.g. bis-homoaromaticity. Unlike Hückel homoaromatics, the Möbius form is intrinsically chiral (disymmetric), promoting a speculation of whether the asymmetric nature of any such Möbius homoaromatic might be utilizable synthetically.
Calculations were performed at the B3LYP DFT level and 6-31G(d,p) or aug-cc-pVTZ basis set level, as implemented in the Gaussian 03 (revision E.01) program.17 AIM critical points, and the molecular graphs that map their connectivity were obtained by exporting a WFN file from Gaussian and importing into AIM200018. The ring critical point coordinates so obtained were used to evaluate the NICS(rcp) values using Gaussian 03 and the GIAO NMR method. ELF surfaces were calculated using Dgrid19 and visualized at differing isosurface values with VMD20 using a FCHK file exported from Gaussian. These files and coordinates are all available via the digital repository entries to be found in the Web-enhanced Table.