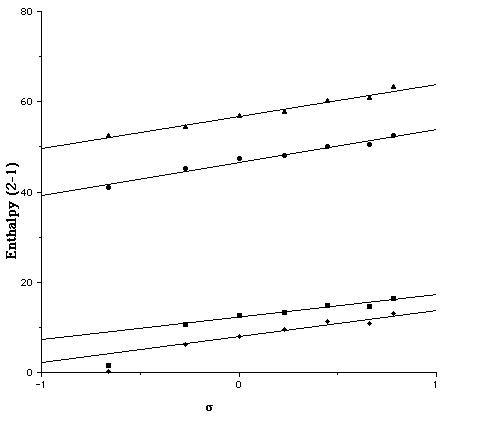
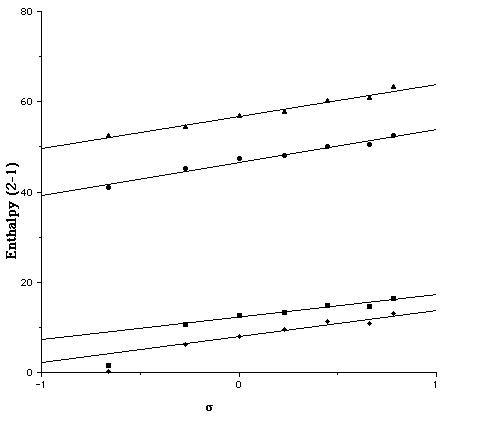
Abstract: AM1 and PM3 SCF-MO/COSMO solvation modelling of the solvatochromic properties of the Rhodamine based colour forming dyes reproduces the known relative stabilities of these molecules and demonstrates how theoretically constructed linear-free-energy relationships could be used in the rational design of new systems.
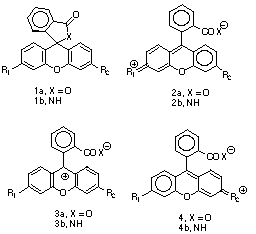
Theoretical studies of systems such as 1 have been limited to spectral studies,[4] rather than to the position of the solvent sensitive equilibrium. In part this has been due to the relatively poor solvation models that can be applied to large organic molecules, particuarly when geometry optimisation is essential. Recent progress in developing continuum solvation models such as the COSMO method[5] now enables calculation of enthalpies and free energies of such equilibria.[6] We show here that application of the COSMO/semi-empirical AM1 or PM3 model enables theoretically estimated linear free energy relationships (LFER) for systems such as 1 to be evaluated, and geometrical responses to solvation to be estimated.
The calculated gas phase enthalpy ([Delta]Hg) for the open zwitterionic forms 2a (R2 = NH2, OMe, H, Cl, CO2, CN, NO2) is 50-56 or or 38-45 kcal/mol higher than 1a at the PM3 or AM1 levels, values similar to the glycine equilibrium.[7 ]For R1=R2=NH2 at the COSMO/AM1 level, the quinonoid form is predicted to be more stable in water [[Delta][Delta]Haq(2a-1a) = -2.7 kcal/mol], as found experimentally[3]. This value is little changed when corrected to [Delta][Delta]Gaq (-2.8 kcal/mol) using the vibrationally estimated entropies. To see how such theoretically derived energetics might be used in linear free-energy relationships, we initially plotted both [Delta][Delta]Hg(2a-1a) and [Delta][Delta]Haq(2a-1a), R1=NH2 against the Hammett [sigma]p value of R2. These plots are reasonably linear (r[2] 0.94 -0.96) for both the AM1 and PM3 methods (Figure 1), suggesting a high degree of self-consistency in the theoretical procedure. Indeed, we expect that such correlations may prove a good test of new parameters derived for other elements.
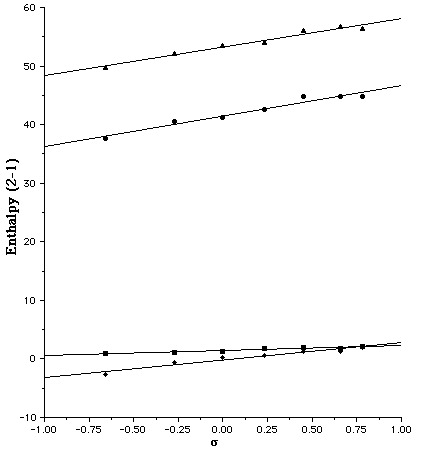
Several interesting trends are discernible from the slopes of these plots. Firstly, for R1=NH2, the gas phase slopes (5.2/AM1, 4.9/PM3) are significantly larger than the COSMO solution values (2.9/AM1, 0.85/PM3). If R1=H this reduction is attentuated from 7.3 (AM1) and 7.1 (PM3) to 5.9 (AM1) and 5.0 (PM3). Secondly, the R1 substituent attenuates the electronic effect of the R2 group (Figure 2). In this, the PM3 effect (e.g slopes of 5.0 and 0.85 for R1 = H and NH2 respectively) is more pronounced than the AM1 effect (5.9 and 2.9).
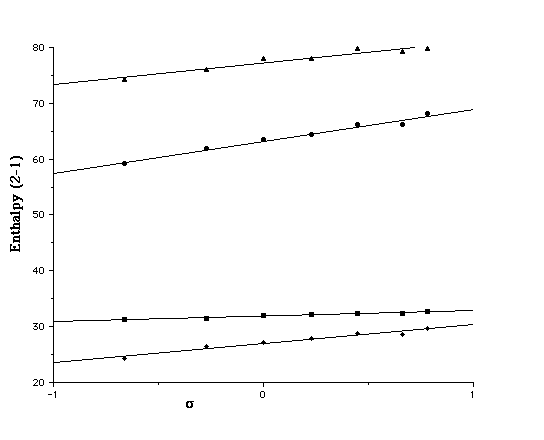
We also investigated the effect of entropy by correcting [Delta][Delta]H to [Delta][Delta]G. Correlating this with the Hammett [sigma]p value produces a slope which is formally equivalent to the Hammett [rho] values. This entropic correction has almost no effect on the slopes derived from [Delta][Delta]Hg, but appears to induce a small increase compared with those derived from [Delta][Delta]Haq, indicating that entropic factors can indeed play a role in free energy relationships. The use of [Delta][Delta]Gaq values also produces more scatter in the Hammett plots, possibly due to errors in calculating low frequency modes in the contributions to [Delta]Saq. In all cases, the point corresponding to R2=CN deviates significantly, suggesting a systematic error in both the AM1 and PM3 for this particular substituent. The corresponding lactams (X=NH) show similar behaviour (Figure 3), although the equilibrium is predicted to favour the closed neutral form by a substantial margin under all circumstances.
The calculated COSMO geometries reveal some interesting trends. With the PM3 method and R1=NH2, all the calculated geometries show bond localisation as in 2, even when both R1=R2=NH2, whereas with AM1 this latter combination and also to some extent R1=NH2, R2=OMe are more delocalised as in 3. In one instance (R1=NH2, R2=Cl, PM3), we were able to locate two valence isomers differing in energy by 17.3 kcal/mol, the lower energy one corresponding to 2 (rNC 1.317Å, rCl-C 1.683Å), the other to 4 (rNC 1.426Å, rCl-C 1.462Å).
For the series R1=H, differing geometrical behaviour was observed. With the exception of R2=NH2 all the geometries were analogous to 3, whilst with R2=NH2 only, localisation to the quinoid form 2 occured at both the AM1 and PM3 levels. This effect is also visible in the Hammett plots, the values of [Delta][Delta]Haq and [Delta][Delta]Gaq for this substituent deviating significantly from the regression line formed by the other substituents (Figure 2). For this reason, these points are excluded from the regression slopes noted above. One explanation for this anomalous behaviour might lie in the neglect in the COSMO model of terms corresponding to the cavitation and dispersion free energies, which are generally taken as being proportional to the solute surface area[8]. Whilst these terms would be expected to cancel for a homologous series of compounds, this would not be true if any unusual changes in surface area between 1 and 2 or 3 due to bond localisation occured. In practice, we found the changes in surface area between 1 and 2 are small and show no correlation with the R1=NH2 substituent. The abnormal behaviour for this system therefore remains unclear.
We conclude that the application of the COSMO method allows the effect of substituents on solvatochromic equilibria involving major changes in substrate polarity to be studied theoretically in a systematic way.
We thank the DGICYT for a postdoctoral studentship (to G. A. S.) and Dr N. Hughes for valuable discussions.
Theoretical calculations were carried out at the restricted Hartree-Fock level (RHF) using the AM1 or PM3 semi-empirical SCF-MO methods, as implemented in the MOPAC 93 program[9], using a relative permittivity of 78.4, with up to 60 surface segments per atom for the COSMO model being used to construct a solvent accessible surface area based on van der Waals radii. The solute charge distribution was evaluated from an atom centred model including charges, dipole and quadrupole moments. All structures were optimized to a gradient normo f < 0.1, using the eigenvector following method. The Keyword LMIN=-100 was used to assist convergence. Enthalpies were corrected to free energies using entropies calculated from a complete vibrational analysis.
References.
1. C. Reichardt, Chem. Soc. Rev., 1992, 21, 147; M. Dolman and I. O. Sutherland, J. Chem. Soc., Chem. Commun, 1993, 1793.
2. P. Gregory, N. Hughes, Eur. Pat. Appl., EP 289122, 1988; N. Hughes, British Pat. Appl 1423346, 1976.
3 V. K. Runov, S. M. Sapezhinskaya, J. Analytical Chem., 1992, 47, 1189; N. O. Mchedlov-Petrosyan, Zh. Fiz. Khim., 1985, 59, 3000; N. S. Poluektov, V. N. Drobyazko, S. B. Meshkova, Zh. Anal. Khim., 1973, 28, 1408.
4. S. Bergamasco, G. Calzaferri, K. Haedener, J. Photochem. Photobiol., A, 1990, 53, R. Hilal, H. Ead, A. Osman, Appl. Spectrosc., 1978, 32, 557.
5. A. Klamt and G. Shürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799.
6. H. S. Rzepa and G. A. Suner, J. Chem. Soc., Chem. Commun., 1993, 1743.
7. H. S. Rzepa and M.Yi, J. Chem. Soc. Perkin Trans. 2, 1991, 531.
8. C. J. Cramer and D. G. Truhlar, J. Comp. Aided. Mol. Design, 1992, 6, 629.
9. MOPAC-93: J. J. P. Stewart, Fujitsu Limited, Tokyo, Japan (1993). Available from Quantum Chemistry Program Exchange, University of Indiana, Bloomington, Indiana.
Captions to Figures.
Figure 1. Plot of the Hammett [sigma]p substituent constant for R1=NH2 for u [Delta][Delta]Haq(2a-1a)/AM1, n [Delta][Delta]Haq(2a-1a)/PM3, l [Delta][Delta]Hg(2a-1a)/AM1 s [Delta][Delta]Hg(2a-1a)/PM3.
Figure 2. Plot of the Hammett [sigma]p substituent constant for R1=H for u [Delta][Delta]Haq(2a-1a)/AM1, n [Delta][Delta]Haq(2a-1a)/PM3, l [Delta][Delta]Hg(2a-1a)/AM1 s [Delta][Delta]Hg(2a-1a)/PM3.
Figure 3. Plot of the Hammett [sigma]p substituent constant for R1=NH2 for u [Delta][Delta]Haq(2b-1b)/AM1, n [Delta][Delta]Haq(2b-1b)/PM3, l [Delta][Delta]Hg(2b-1b)/AM1 s [Delta][Delta]Hg(2b-1b)/PM3.