![[4]phenylene](images/4phenyln.gif)
| ![[4]phenylene](images/TBHB.gif)
|
| [4] Phenylene | TBHB |
|---|
Figure 3.1
-
The purpose of this project is to study the Trisbicyclo[2.1.1]hexabenzene with semi-empirical methods and to measure the effect of the localization of the electrons on Diels-Alder reactions. It is well known that Diels-Alder additions on benzene are very difficult because of the loss of aromaticity during the reaction. It would probably be easier on a cyclohexatriene motif, but steric effects have to be taken into account too.
- Semi-Empirical molecular studies
Unless otherwise specified, all numerical parameters have been extracted from the PM3 geometries using MOPAC93.
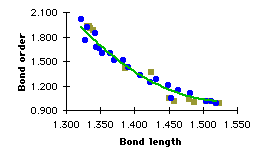
It is easy to say if a molecule, an ion or a radical is aromatic or not, it is more difficult to define precisely and measure this aromaticity. In the fourth part, we will explain how we can try to measure this aromaticity. However we know that aromatic bonds are neither single nor double bonds. They are intermediate between alkyl single bonds and alkene double bonds. Bond lengths are very good parameters, by which to classify bonds. For instance, the carbon-carbon bond length is 1.504 Å (Bond order : 1.014) in ethane, whereas it is 1.322 Å (Bond order : 2.007) in ethylene (Table 3.1). Every carbon-carbon bond in benzene is 1.391 Å long (table 3.1). X-ray data are 1.54 Å for ethane, 1.33 Å for ethylene and 1.40 Å for benzene. Despite the lack of accuracy of these semi-empirical calculations, we can still classify bonds and decide if a molecule is aromatic or not.
[4]Phenylene (Figure 3.1) has a cyclohexatriene motif, double bonds are 1.33 Å long, and single bonds belonging to the 4-membered rings are 1.512 Å long. The difference between the two bond lenghts is 0.182 Å. Unfortunately these compounds cannot be used to make specific reactions on the central ring because it is surrounded with other aromatic rings.
However, when we use alkyl groups to force benzene to forgo its aromaticity, the aromatic ring remains the reactive entity. TBHB is obviously a good solution to achieve bond alternation. The single bonds in the bicyclic rings are strained and therefore the sigma-electrons are held less tightly by the nuclei. They repel the pi-eletrons away from the bicyclic rings, forcing them to localize. The difference between the two bond lengths is 0.116 Å (X_ray : Å[18]). Comparison with the value we calculated for [4]Phenylene reveals that we only have a partial lost of aromaticity. However this should be enough to change the reactivity of the benzene ring.
We decided to study the steric and electronic effects of the bicyclic rings. We modelled two other compounds with respectively one and two bicyclic rings (Monobicyclo[2.1.1]hexabenzene - MBHB and Dibicyclo[2.1.1]hexabenzene - DBHB). Detailed results of bond lengths and orders are given in Table 3.1.
|
|
|
Table 3.1 : Bonds lengths and Bonds Orders in varied molecules.
-
In Table 3.1, the bond numbers for TBHB and MBHB are indicated in figure 3.2. For hexatriene, the value corresponds respectively to the central double bond, to the single bonds and to the double bonds at the extremities.
- Diels-Alder reactions
- Reaction with a diene (butadiene)
| 
|
| DBHB | MBHB |
Figure 3.2
- When different transition states and products could be found for exo and endo attacks, they were in reported in the graphs. This does not mean that the two products exist, but only that there are two local minima in the energy map. The energy barrier between the two conformation may be very small, and we will observe only the most stable product.
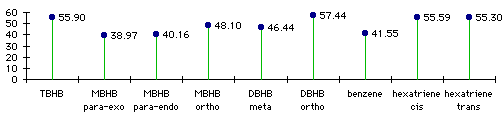
|
Graph 3.2 : Activation Energies (Diels-Alder addition with butadiene), kCal/mol
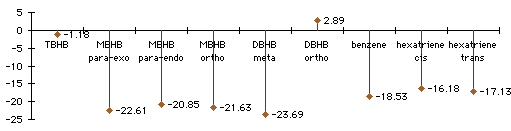
|
Graph 3.3 : Reaction enthalpies (Diels-Alder addition with butadiene), kCal/mol
-
With TBHB (and also with DBHB in the ortho position) steric effects are so important that the Diels-Alder addition is endothermic despite the formation of two new bonds. You can hardly have a Diels-Alder addition on a double bond between two bicycles. Where steric effects are less significant, in MBHB or in DBHB, the Diels-Alder addition can be easier. The activation energy with MBHB in the para position is 3kCal/mol less than it is with Benzene. The steric effects are compensated by the loss of less aromaticity during the reaction. With smaller groups than these bicycles, it would probably be easy to have a Diels-Alder addition on a benzene ring.
- Reaction with a dienophile (ethylene)
Addition on the central bonds in hexatriene is very difficult (even more so than with benzene). This is due to the loss of conjugation : the product is not conjugated whereas the reactant was fully conjugated. This is the advantage of having a cyclohexatriene motif, where two double bonds remain conjugated.
These reactions are a lot more difficult than the standard Diels-Alder addition of ethylene and butadiene. This is due both to the loss of aromaticity and conjugation during the reaction and to steric effects. We could facilitate these additions with electron-donating groups on the diene and electron-attracting groups on the dienophile.
| 
|
| DBHB | MBHB |
Figure 3.3
|
Graph 3.4 : Activation Energies (Diels-Alder addition with ethylene), kCal/mol
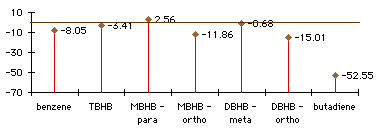
|
Graph 3.5 : Reaction enthalpies (Diels-Alder addition with ethylene), kCal/mol
-
Graph 3.5 shows that the reaction enthaplies of the Diels-Alder additions of ethylene to bicyclic-substituted benzene ring are greater than or equal to the addition to benzene. There is no gain in using a partial localization of the double bonds. We can see that the reactions are not very exothermic, or even endothermic. This is probably due to steric effects, because we are forming a [2.2.2]bicyclic compound, whereas the addition of butadiene on an aromatic ring gives a [4.2.2]bicyclic compounds that is less strained.
- Measuring the lost of aromaticity
Comparing the transition states of the two kind of addition (with ethylene and with butadiene), we see that addition of ethylene seems to be easier. This is due to steric effects too. Ethylene is smaller than butadiene and can go closer to the benzene ring without encountering the bicyclic groups.
At first glance, some results may be surprising : addition of ethylene on MBHB is easier on the ortho position than on the para. Since the product of the para addition has a double bond that is localized in the [2.1.1]bicyclic fragment, this strain destabilizes both the transition state and the product. For exactly the same reason, the ortho addition of ethylene on MBHB is easier than the meta addition, despite the sterical effects.
Study of the Diels-Alder additions of TBHB and derivate compounds has shown that what we gain with the localization of the double bonds in the benzene ring can be lost with the steric effect due to the size of the groups used to produce the cyclohexatriene motif. We should use smaller groups. Because it has been proved[15] that other alkyl groups are unlikely to produce the bond alternation, we would have to introduce hetero atoms. This could help the benzene to forgo its aromaticity and this too could facilitate the Diels-Alder addition.
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
|
table 3.2
- The energy difference for an addition of one bicycle on benzene or subtituted benzene (45 kCal/mol) is the same as for an addition on ethene. It should be somewhere between the energy difference for ethane and for ethene: about 42 kCal/mol. This difference (45 - 42 kCal/mol) can easily be explained with the loss of aromaticity in each addition of a bicycle to the benzene.
- Each addition of a bicycle has the same effect on the heat of formation: it increases by 45kCal/mol. This tends to prove that the same amount of aromaticity is lost with the addition of each bicycle.
Two different observations can be made on table 3.2 :
To confirm this evaluation, we will simulate some reactions on benzene and TBHB. We measure the aromaticity of the benzene through a simple thermodynamic cycle that is described in figure 3.4
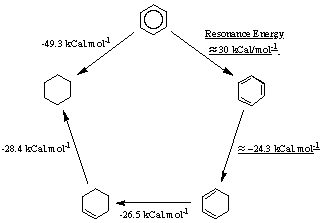 |
Figure 3.4 : Estimation of the resonance energy in Benzene
It is possible to estimate how much more stable benzene is compared to a hypothetical "cyclohexatriene". The heat of hydrogenation of the double bond in cyclohexene is -28.4 kCal/mol. The one for a double bond in 1,3-cyclohexadiene is -26.5 kCal/mol. By a simple extrapolation, we might expect the heat of hydrogenation of one of the double bonds in cyclohexatriene to be about : -26.5 + (-28.4-26.5) = -24.5 kCal/mol.
By comparison with the heat of hydrogenation in benzene, we find that benzene is about -49.3 - (-28.4-26.5-24.5) = 29.9 kCal/mol more stable than it would be if it had the cyclohexatriene structure. This stabilization energy defines the resonance energy of benzene, that is the difference in energy between the real benzene and that of a single principal Lewis resonance structure.
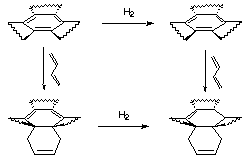
The same argument cannot be followed exactly for TBHB, on account of the strain that is being added or released with each hydrogenation, and the different isomers which are produced after each hydrogenation. We use an another method that takes into account the strain introduced or released after the hydrogenation, and that only deals with one hydrogenation, so there are fewer isomers.
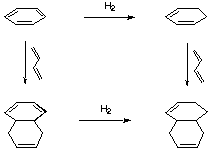
| 
|
Figure 3.5 : Estimation of resonance energy in TBHB
-
Here is the procedure we have employed to estimate the resonance energy in TBHB (Figure 3.5) :
-
The reaction enthalpy of the hydrogenation of TBHB is supposed to have three components :
- A classic term for the hydrogenation of a double bond
- A term accounting for the lost of aromaticity
- A term accounting for the strain
- The reaction enthalpy of the hydrogenation of the Diels-Alder adduct of TBHB and butadiene has only the hydrogenation and the strain components, because it is not aromatic any more.
Hr2 = 166.01 - 189.06 = -23.05 kCal/mol - The difference between the reaction enthalpy calculated in i. and ii. corresponds to the aromaticity and a correction due to the fact that the two hydrogenations are different.
H3 = -11.07 - (-23.05) = 11.98 kCal/mol - To evaluate this correction, we follow the exact same steps with benzene.
Hr4 = 20.30 - 23.39 = -3.09 kCal/mol
Hr5 = 10.24 - 35.85 = -25.61 kCal/mol
H6 = -3.09 - (-25.61) = 22.51 kCal/mol - The difference between the two final values corresponds to the destabilisation of TBHB in comparison with the benzene, i.e. the lost of aromaticity :
H = 11.98 - 22.50 = -10.52 kCal/mol
. - Conclusion
The use of bicyclic substituents to generate a cyclohexatriene motif is a new area of research . The trisbicyclo[2.1.1]hexabenzene is the only compound that has been synthetised and studied. It cannot easily be used to facilitate reactions like Diels-Alder additions on aromatic rings, but we can reasonably think that some derived molecule would be found that will permit a full localization of the pi-electron cloud. A wide range of alkyl substituents have been studied, therefore we have to introduce some hetero atoms. Computer models will be useful to decide which molecule is worth to synthetizing.
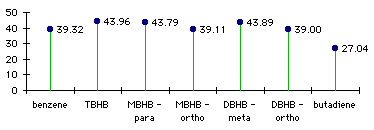
To understand how benzene forgoes its aromaticity in TBHB, we can have to look at the energy levels. On graph 3.6 we can see that there is no major difference between benzene and the mono-, di- and trisbicyclo[2.1.1]hexabenzene. This confirms the fact that the aromaticity is lost progressively with the addition of each bicycle (table 3.2).
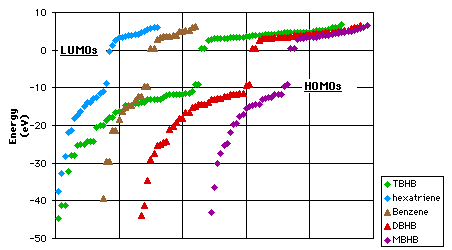 |
Graph 3.6 : Energy levels
Mopac 93/ PM3
*We have only tried to estimate the destabilization in comparison with benzene. Therefore we did not differentiate between the empirical resonance energy, which refers to a cyclohexatriene structure with alernating bond lengths, and the delocalization energy which refers to a structure where all bonds, single or double, have the same lengths .To calculate the delocalization energy, we could try to rebuild the pi molecular orbitals (and renormalize them), keeping the nuclear geometry and the sigma-orbitals unchanged and then calculate the SCF energy using ab initio programs such as Gaussian[19].
| Previous | Table of Contents | Next |