Nature of the Bonding in C2/Ti2,
N2/V2, Cr2 and related
species.
Henry S. Rzepa
Department of Chemistry, Imperial college London
This short tutorial presents an analysis of the bonding in some simple
diatomic species, contrasting the behaviour of these species deriving from
the main group elements of the periodic table and the corresponding transition
series.
Dicarbon and Dititanium
|
Titanium and carbon are related by virtue of their
relationship in the periodic table; carbon occupies the
main group and titanium the same position in the
transition series. Each has four valence electrons, but
when these are combined to form bonds, they achieve
rather different results.
Atomic carbon is usually said to organise its valence
electrons into a
2s22p12p12p0
configuration, which gives total of eight electrons (for
two atoms). Symmetric and antisymmetric combinations of
the (doubly occupied) pure 2s atomic orbitals (AOs) would
result in a bonding and antibonding σ-combination of molecular orbitals, both doubly occupied and
the resulting bond orders of which would exactly cancel. The two singly occupied 2p orbitals
overlap in parallel fashion to form two bonding doubly occupied π molecular orbitals which contribute
a net bond order of two. This gives us the
(text book) picture of predicting a total bond order of 2 for
this molecule (which is nevertheless unusual, in having
only π bonds, with no underlying σ bond).
However, another way thinking about it is to start
from a
2s12p12p12p1
atomic orbital configuration. Whilst this (initially) takes a little
more energy, it is hoped this energy will be (more than) recovered
in any eventual
molecular orbitals formed by combining the AOs. Firstly a bonding orbital is formed
by end-on (σ) overlap of (mostly) the (singly
occupied) 2s atomic orbitals, Two equal (degenerate) molecular orbitals are
formed by parallel (π) overlap of two of the
2px/y orbitals on each atom. The remaining
2pz1 orbital starts to overlap
end-on. This is where things start to get less simple. 
|
| Dicarbon, with triple bond,
comprising: |
| Two bonding 2pπ (parallel p) |
Non-bonding 2pσ (end-on p) |
One Bonding 2sσ |
 |
 |
 |
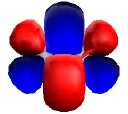
| Dititanium, with quadruple bond,
comprising: |
| One Bonding 3dδ (parallel
d) |
Two bonding 3dπ (end-on d) |
One Bonding 4sσ |
 |
 |
 |
|
|
The end-on overlap is shown in
Scheme 1, in which the
two 2p orbitals are shown vertically offset for clarity.
In 1 the two pz orbitals approach out
of phase. As the two opposite phases begin to interact
(2) they eventually get close enough that the two
out-of-phase lobes overlap maximally, and hence 3
would correspond to an anti-bonding overlap. But, as the two AOs get even closer
(4) a new in-phase overlap begins to neutralise
the original out-of-phase overlap until in 5 they
are more or less balanced. You could perform this
exercise starting from an initial in-phase approach, but the end
result would be the same. At this point (5) we have a
non-bonding orbital! If the (2s) σ bonding orbital is
added to the two (2p) π bond orders, the overall bond order
reaches 3! (albeit a situation rarely if ever shown in
text books). Clearly, its not quite as simple as that,
since one must also superimpose upon this picture some
degree of s/p hybridisation (which in effect mixes the
two starting atomic configurations to achieve something
in between, in the trade this is known as a multi-reference configuration), and obviously the final bond length between the two carbon
atoms determines the degree of overlap. Needless to say, when a full
quantum-mechanical calculation is done to calculate all these effects,
the net result is something close to a predicted triple
rather than a double bond for C2! |
|
Titanium plays the same game, this time starting from an
atomic electronic configuration of
4s13d13d13d1.
Now each of the single electrons can pair up (yes you
guessed, we are forming a singlet state here, see below
for a reality check!) to form only a bonding interaction.
Firstly the two 4s1 electrons pair up to
form a single σ bond. Next two of the 3d1
d-orbitals overlap "end-on" to form two "π" bonds
formed by d-orbitals. Unlike the end-on overlap of the
(non-bonding) 2p orbitals in C2, this
combination is strongly bonding. The final 3d1
orbital on each atom now overlaps in parallel fashion to
form a final so-called δ bond. The overall bond order is
four, i.e.. a quadruple bond, a higher order than with
singlet C2 due to the difference in nodal properties
between the carbon 2pz and the titanium 3d
atomic orbitals.
Reality Check: Of course, Ti2 as a real species does not
actually have a quadruple bond (and a singlet ground
state). In fact, it forms a high spin
triplet state, where two of the electrons uncouple their
spins, with a corresponding decrease in the bond order
from four to three. The real C2 molecule is however
a singlet ground state, i.e.. all the electrons are spin
paired; the unpaired triplet state being somewhat higher in
energy.
|
Dinitrogen and Divanadium
|
These two elements also have the same periodic table
relationship. The nitrogen atom really does have an
atomic configuration of
2s22p12p12p1.
Here, the 2s/2p mixing is much less than with carbon (due
to the greater energy difference between the two) and the
(mostly) 2s orbitals combine to form bonding and
anti-bonding combinations, both of which are populated
with 2 electrons each. This results in a zero combined
bond order (unlike dicarbon where this combination
overall results in a bond order of 1). Each of the three
(mostly) 2p orbitals form bonding combinations of one
in-phase end-on σ overlap and two π type
overlaps, and the six electrons populating these result
in a total bond order of 3, but now originating in a
rather different way than that of carbon.
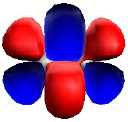
Vanadium has an atomic configuration of
4s13d13d13d13d
1. Two of the d AOs overlap in parallel fashion to
form two δ bonds. The 4s orbitals overlap to form a
σ bond and the last two π bonds form by end-on
d-overlap. Thus the complete absence of the 2s
bonding/antibonding cancellation takes the V2
bond order to five!
Reality Check
V2 also does not actually have a pentuple
bond, since like Ti2, the ground state is a
triplet species and not a singlet.
|
| Nitrogen, with triple bond,
comprising: |
| One Bonding 2pσ (end-on p) |
Two bonding 2pπ
(parallel p) |
 |
 |
| Divanadium, with pentuple bond,
comprising: |
| Two Bonding 3dδ (parallel
d) |
One Bonding 4sσ |
Two bonding 3dπ (end-on d) |
 |
 |
 |
|
Onwards to Dichromium
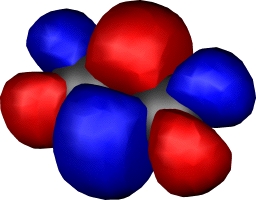
| Dichromium, with hextuple bond,
comprising: |
| Two Bonding 3dπ (end-on d) |
One bonding 3dσ (end-on
dz2) |
Two bonding 3dδ (parallel
d) |
One Bonding 4sσ |
 |
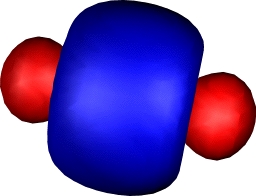 |
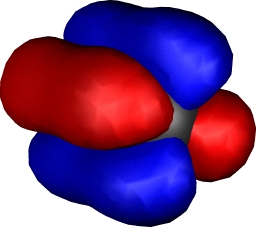 |
 |
|
Yes, you guessed it, Cr2
continues the trend of Ti2 and V2 in
having a hextuple bond. If atomic chromium is considered as
having the configuration
4s13d13d13d13d
13d1, the resulting bonds comprise one
σ bond formed from the 4s orbitals, two π and two
δ bonds formed by respectively end-on and parallel
overlap of the d-orbitals, and (additional to V) a σ
bond formed by end-on overlap of the dz2
orbital. This time, the ground state really is a closed shell
low spin singlet. Despite the remarkable bond order, it has
a relatively weak bond strength of about 33 kcal/mol! In
effect, all those twelve electrons crammed into the small
diatomic region do not result in strong bonds.
|
A Closer and perhaps different look at C2,
N2 and other species.
Another way of looking at the bonding in C2 is to
transform the molecular orbitals to so-called localised
orbitals. The following diagrams illustrate such orbitals
transformed according to a scheme proposed by Pipek and Mezey.
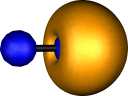
Two localised orbitals for dicarbon appear essentially
identical to the molecular orbitals and correspond to the
orthogonal π orbitals. The two end-on molecular orbitals
jointly transform to two (identical) localised orbitals (unlike
the MOs which are different), each having significant density
in the C-C region (i.e.. each of these localised orbitals
contributes about half a bond order). This is another way of
achieving the quantum mechanical sp hybridisation
referred to above.
| Pipek-Mezey Localised orbitals |
| Carbon |
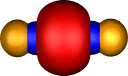
Nitrogen |
| Two π |
Two σ |
Two π |
Two σ |
One σ |
 |
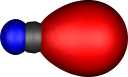 |
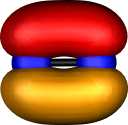 |
 |
 |
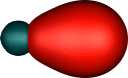
| Boron B22- |
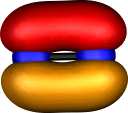
Nitrogen N22+ |
| Two π |
Two σ |
Two π |
Two σ |
 |
 |
 |
 |
Contrast this with nitrogen. The two π orbitals are the
same as before, but now there are two end-on (again identical)
σ localised orbitals which consist mostly of 2s character, neither
of which shows any bonding in the N-N region (this is
equivalent to saying that doubly occupied bonding and
anti-bonding 2s combinations cancel). This situation
corresponds to the 2s22p12p12p0
atomic configuration discussed for carbon; it is favoured
because the greater electronegativity of N means an electron
prefers the 2s to a 2p orbital, i.e.. The greater nuclear charge
on nitrogen differentiates more effectively between 2s and 2p
atomic orbitals. Unlike carbon, nitrogen has a third
occupied 2pz1 atomic orbital, which forms a
localised and clearly bonding orbital of largely 2p end-on
character. Because of the greater nuclear charge on N, the 2p
atomic orbital is also rather "smaller" than that for carbon, and so the onset of
non-bonding character which could arise when two of them
overlap end on (scheme 1 above) is less advanced for N.
The effect however can be detected, since the resulting N-N bond
length is actually rather longer than it ought to be (despite often being cited
as the strongest bond). If
N2 is protonated to form a diazonium ion,
HN2+, the N-N bond length actually
shrinks because the H+ polarises the 2pz
orbital, making the σ-bond stronger (this now is the record holder
for bond strength!).
Going in the opposite direction, boron (as B- to make it isoelectronic with C) would be expected to
increase the 2s/2p mixing because of the smaller nuclear charge
(i.e.. favouring even more the
2s12p12p12p1
configuration). Thus the corresponding 2spz end on
orbital for the molecule B22- (which is
isoelectronic with C2) is now bonding rather than
non-bonding, and the two resulting localised orbitals
each contribute almost a whole single bond order rather than around half. This little
molecule has a total predicted bond order of four (two
π, two σ), although perversely the B-B bond length is actually longer
than the C-C length.
Moving back to N22+,
the positive charge has the effect of further contracting the
size of the valence atomic orbitals. Perhaps the 2pz
orbital is so small that it too avoids the non-bonding region
(Scheme 1). At any rate, this molecule too has a total predicted bond
order of around 4 (and that too has not made it into the text
books!).
Literature
- Gutsev, Gennady L.; Bauschlicher, Charles W. Chemical
Bonding, Electron Affinity, and Ionization Energies of the
Homonuclear 3d Metal Dimers. Journal of Physical Chemistry
A (2003), 107(23), 4755-4767.
- Barden, Christopher J.; Rienstra-Kiracofe, Jonathan C.;
Schaefer, Henry F., III. Homonuclear 3d transition-metal
diatomics: A systematic density functional theory study.
Journal of Chemical Physics (2000), 113(2),
690-700.
Viewing the orbitals
To demonstrate the 3D nature of these orbitals, each
thumbnail image above is linked to a 3DMF file. To view these
orbital models, you will need a 3DMF viewer such as 3DMFPlugin (a browser plugin), 3DMF
Optimizer or Geo3D (Macintosh applications) or 3DMF Viewer for Windows.
Windows Users
Windows users must follow this procedure
- install the
QuickDraw3D libraries from Apple
- Download this
plugin
- Unzip the contents of NPQuick3D32.ZIP and copy the single
file (npquick3.dll) to the plugins directory of your browser.
The path to this will be something like C:\Program
files\Mozilla\Plugins. We recommend a browser such as Mozilla
or FireFox. Internet Explorer no longer supports such
plugins, and should not be used for this purpose.
(C) H. S. Rzepa, 2004.
























