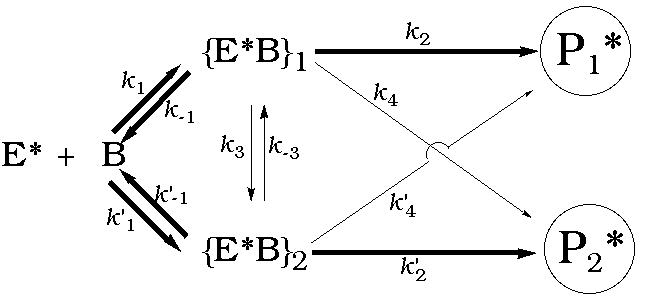
 Scheme 1: Kinetic scheme of the isoinversion principle
Scheme 1: Kinetic scheme of the isoinversion principle
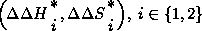 . The program is capable of handling
systems with (or without) inversion points , calculating T_inv,
. The program is capable of handling
systems with (or without) inversion points , calculating T_inv,
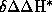 and
and 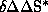 and T_i (from the
compensation diagram). The selectivity- relevant parameters (e.g. solvent,
reactants, products) may then be stored in the database.
and T_i (from the
compensation diagram). The selectivity- relevant parameters (e.g. solvent,
reactants, products) may then be stored in the database.
The selectivity of chemical reactions is a major challenge in organic chemistry. Despite diastereo- and enantioselctivity also chemo- and regioselectivity are of interest. During our temperature dependent measurements on the Paternò-Büchi reaction we found that the diastereoselectivity did not increase monotonously with decreasing temperature. This means no simple correlation in the corresponding Eyring plots was obtained.
The selectivity of a chemical process depends on the correspondence of activation enthalpy and activation entropy influences. The isoinversion principle is the first dynamic model for understanding the origin of selectivity in reactions which proceed with more than one selection level by the discussion of competing enthalpy and entropy influences. The basis of the isoinversion principle is depicted in the following kinetic scheme. The scheme is valid only for chiral systems, but is applicable to regio- and chemoselective problems very easily, by changing the reactants.
 Scheme 1: Kinetic scheme of the isoinversion principle
Scheme 1: Kinetic scheme of the isoinversion principle
A starting material B, containing for instance a prochiral element, reacts with a chiral substrate or catalyst E* to afford the diastereomeric intermediates {E*B}1 and {E*B}2, in different rates and proportions. The formation of these intermediates represents the first level of the selection process. The intermediates can react further to the diastereomeric products P1* and P2* or are cleaved back to the starting materials. These educts can be fed back into the reaction cycle again. Alternatively, the conversion of one diastereomeric intermediate into the other is conceivable. Hence the second selectivity level is made up of the possibility of retrocleavage and that of interconvertibility of the intermediates.
The evaluation of the temperature dependent measurements is performed by a modified EYRING equation:
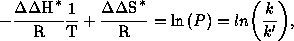
Equation1: Modified EYRING equation
k: overall rate constant of the formation of the major isomer
k': overall rate constant of the formation of the minor isomer
T: absolute temperature
R: gas constant
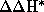 : difference of activation enthalpies
betwen the competing reaction channels
: difference of activation enthalpies
betwen the competing reaction channels
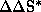 : difference of activation entropies
between the competing reaction channels
: difference of activation entropies
between the competing reaction channels
The temperature-dependent analyses depend on the measurement of the ratios of
the reaction products formed, which may be stereoisomers (enantiomers,
diastereomers), regioisomers, or result from a chemoselective reaction. The
modified EYRING equation is derived from the well known EYRING equation to
allow the determination of activation parameters 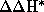 ,
,
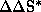 for competitive reaction channels by correlation
with rate constants k and k'. The existence of two independent linear regions
with a corresponding inversion temperature (Tinv) in the Eyring plots implies a
process that proceeds on more than one selection level.
for competitive reaction channels by correlation
with rate constants k and k'. The existence of two independent linear regions
with a corresponding inversion temperature (Tinv) in the Eyring plots implies a
process that proceeds on more than one selection level.
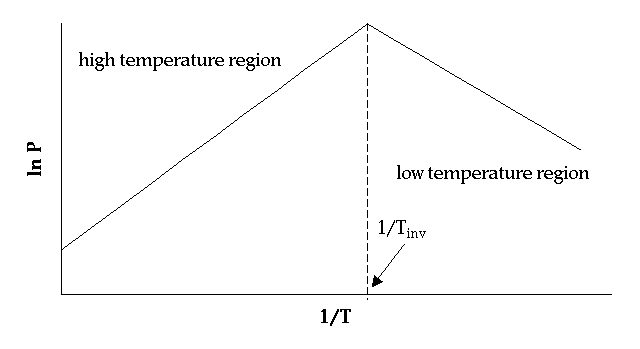
Figure 2: Schematic representation of an EYRING plot for one particular reaction pair
Because of the appearance of inversion temperatures (Tinv), two new sets of
parameters 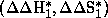 for
T>Tinv and
for
T>Tinv and 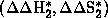 for T<Tinv are available which correspond to enthalpy and entropy in each
of the selectivity steps. By simple substraction of the activation parameters
for the high and low temperature regions (T>Tinv and T<Tinv) one obtains
the new parameters
for T<Tinv are available which correspond to enthalpy and entropy in each
of the selectivity steps. By simple substraction of the activation parameters
for the high and low temperature regions (T>Tinv and T<Tinv) one obtains
the new parameters 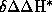 and
and
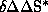 . These represent the change in dominance
of enthalpy and entropy in the partial selectivity steps within one system. If
these new parameters
. These represent the change in dominance
of enthalpy and entropy in the partial selectivity steps within one system. If
these new parameters 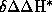 and
and
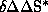 for all systems of a reaction are plotted
on an enthalpy/entropy diagram a strictly linear correlation is observed for
all systems studied for this reaction. The linear correlation in the
for all systems of a reaction are plotted
on an enthalpy/entropy diagram a strictly linear correlation is observed for
all systems studied for this reaction. The linear correlation in the
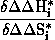 is called isoinversion relationship. The gradient of the line in the
isonversion diagram has the dimension of a temperature, which is defined as the
isoinversion temperature Ti:
is called isoinversion relationship. The gradient of the line in the
isonversion diagram has the dimension of a temperature, which is defined as the
isoinversion temperature Ti:
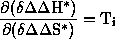
Equation2: Definition of the isoinversion temperature Ti
This temperature is a characteristic constant for the selectivity of the reaction studied. Its practical significance is that at this temperature the optimal value of a selectivity for a particular reaction is to be expected.
An important example for the application of the isoinversion principle is e.g. the osmium mediated cis-hydroxylation
The mechanism of the reaction is not yet totally understood. Two mechanisms discussed have been proposed, a stepwise [2+2] and a concerted [3+2] mechanism [7-17].
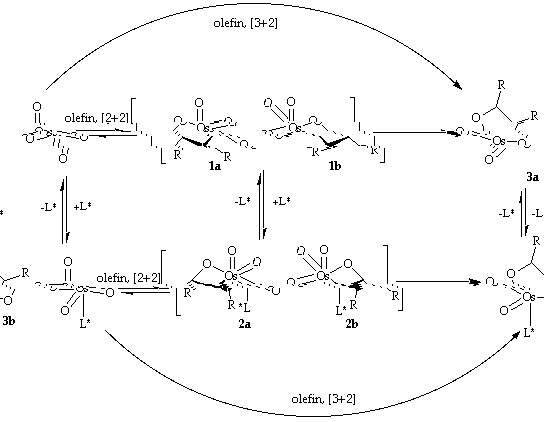
Scheme 2: Postulated mechanisms of the dihydroxylation
In the [2+2] mechanism, the olefin is first coordinated to the osmium atom and rearranges to the osmaoxetane 1. Then rearrangement to the five membered cyclic glycolate 3a takes place . Coordination of an amine ligand L* results in 2, which rearranges to the glycolate 3b much easier than 1. This explains the acceleration of the osmylation by addition of an amine ligand. The [3+2] mechanism proceeds via a concerted formation of the glycolate (3a resp. 3b) without the formation of an osmaoxetane. In the case of the catalytic process hydrolysis of the glycolate and reoxidation of the Os(VI) species takes place [11],[18].
SHARPLESS and GÖBEL [9] investigated the temperature dependence of the enantioselectivity for the stoichiometric process. The use of the stoichiometric variant has the advantage that consecutive processes like hydrolysis of the glycolate ester and reoxidation do not influence the selectivity of the process. The investigation was performed using different olefins and ligands. It is obvious that in all cases two linear regions appear in the corresponding Eyring plots. This means that the observed enantioselectivity results from two levels of selectivity. The results are consistent with a stepwise mechanism (which could be the [2+2] mechanism), but rule out the concerted [3+2]-mechanism the way it is proposed now, because this is dependent only on the difference of activation energies of the two diastereomeric transition states. The two levels of selectivity are proposed to be (i) the formation of the two diastereomeric oxetanes 3a and 3b and (ii) the rearrangement of the osmaoxetanes to the glycolates 4a and 4b. Dependent on the reaction temperature one of the two reaction steps is dominant in each temperature region.
The evaluation unit enables the user to perform the calculations necessary
for the Eyring plots. After measuring the temperature-dependent values, monitoring the relative amounts of the products and the temperature, the chemist enters the measured values into a WWW form.
Depending on whether he or she expects an inversion point, the number
of linear areas can be set to 1 (no inversion point) or 2 (one inversion point). The system then calculates the corresponding parameter values
and displays the Eyring plot in results in pairs of parameters,
After having finished the prototypical implementation of the evaluation component, we are currently working on the database that is to contain the relevant data. Due to the fact that different users will have different needs concerning the way they retrieve data from the database model that has been
formalized with the aid of 1. Kethers, S. ECCC 941994.
2. Buschmann, H. Thesis RWTH Aachen 1992.
3. Hoffmann, N. Thesis RWTH Aachen 1992.
4. Buschmann, H. Scharf, H.-D.; Hoffmann, N.; Esser, P. Angew. Chem. Int.
Ed. 1991, 477.
5. Buschmann, H.; Scharf, H.-D.; Hoffmann, N.; Plath, M.W.; Runsink, J. J.
Am. Chem. Soc. 1989, 111, 5367.
6. Buschmann, H.; Hoffmann, N.; Scharf, H.-D. Tetrahedron Asym.
1991, 2, 1429.
7. Jorgensen, K.A.; Schiott, B. Chem. Rev. 1990, 90,
3329.
8. Norrby, P.O.; Kolb, H.C.; Sharpless, K.B. J. Am. Chem. Soc.
1994, 116.
9. Göbel, T.; Sharpless, K.B. Angew. Chem. Int. Ed. Engl.
1993, 32, 1329.
10. Mc Grath, D.V.; Makita, A.; Sharpless, K.B. manuscript in preparation.
11. Kwong, H.L.; Sorato, C.; Ogino, Y.; Sharpless, K.B. Tetrahedron
Lett. 1990, 31, 2999.
12. Kolb, H.C.; Andersson, P.G.; Sharpless, K.B. J. Am. Chem. Soc.
1994, 35, 1278.
13. Lohray, B.B.; Bhushan, V.; Nandanan, E. Tetrahedron Lett.
1994, 35, 4209.
14. Corey, E,J.; Noe, M.C. J. Am. Chem. Soc. 1993, 115,
12579.
15. Corey, E,J.; Noe, M.C.; Sarshar, S. Tetrahedron Lett. 1994,
35, 2861.
16. Corey, E.J.; Noe, M.C.; Grogan, M.J. Tetrahedron Lett.
1994, 35, 6427.
17. Becker, H.; Ho, P.T.; Kolb, H.C.; Loren, S.; Norrby, P.-O.; Sharpless,
K.B. Tetrahedron Lett. 1994, 35, 7315.
18. Wai, J.S.M.; Markó, I.; Svendsen J.S.; Finn, M.G.; Jacobsen, E.N.;
Sharpless, K.B. J. Am. Chem. Soc. 1989, 111, 1123.
[19] Brunne, J.; Hoffmann, N.; Scharf, H.-D.: Tetrahedron Lett. 1994, 50, 6819.
[20] Brunne, J.: Thesis RWTH Aachen 1994.
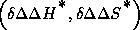 . The consideration of several systems and calculation of their corresponding
. The consideration of several systems and calculation of their corresponding 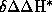 and
and 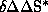 yields the
compensation diagram which can also be calculated with the aid of the computer system.
yields the
compensation diagram which can also be calculated with the aid of the computer system.
Notes
1. We plan to make a prototypical version of the system available during the ECTOC conference.
2. Theoretically, it is possible to have more than one inversion point [19-20].
3.Clicking on the plot results in a monochrome or color postscript version of the plot (which could then be printed or saved easier from Mosaic).