Electronic structure of tetrahydro-v-tetrazines
Institut für Organische Chemie, Universität GH Essen, Germany
Introduction
Photoelectron (PE) spectroscopy [1]
We have measured the
He(I) photoelectron spectra of the tetrazines
1 [2],[3] and 2.
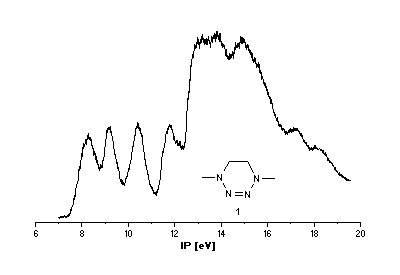
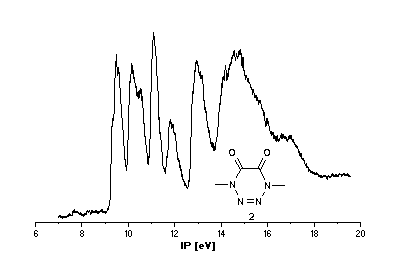Interpretation of PE spectra usually requires correlation of measured
ionization potentials and calculated orbital energies using
Koopmans' approximation [4]. Molecular orbital energies are taken from
semiempirical quantum chemical calculations like PM3 [5]. For tetrazines
1 and 2, this approach does not give satisfactory results.
Tetrazine 1
Semiempirical Calculations
PM3 calculations
lead to two conformers for
1, the half-chair is more stable by 0.84 kJ mol-1. In both, lone pairs
on N(1) and N(4) occupy axial positions which shows that the 2-tetrazene moiety
is only little affected by the conformational change. Therefore, its orbital energies should
not be influenced much either. However, this expectation is not met by the PM3 results.
Calculated spectra of the two conformers differ considerably (Scheme 1) and correlation
coefficients R2 of a linear regression with ionization potentials
are rather poor (0.9077 for the half-chair, 0.9333 for the boat).
With respect to the enthalpy difference, the experimental spectrum
should be that of the mixture of both conformers and according
to PM3 should be complex in the low energy region.
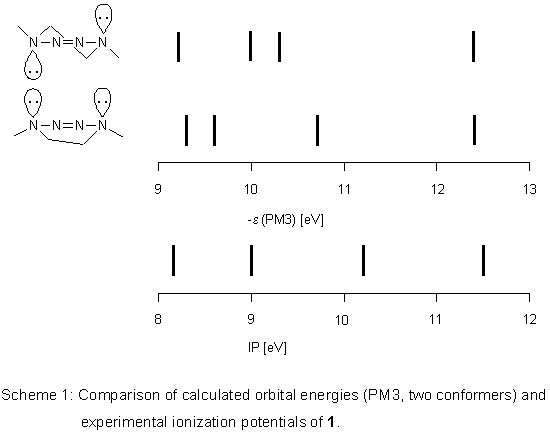As this is not the case,
we undertook higher level calculations in order to better explain the experimental data.
Ab initio calculations
For the hypothetical,
unsubstituted tetrahydro-v-tetrazine 1h, we performed
ab initio
HF and - assuming electron correlation could be important - MP2 calculations
with the basis set 6-31+G*.
Again, unexpectedly, we obtained similar results regarding orbital
energies of the conformers (as for PM3 calculations on 1).
For MP2, the differences in orbital energies of the conformers
were even more pronounced. When we employed the hybrid method
Becke3LYP
[6] of the density functional theory (DFT) using the
same basis set as above, the situation changed. In contrast to
HF and MP2, the two conformers of 1h have almost the same
orbital energies (Scheme 2).
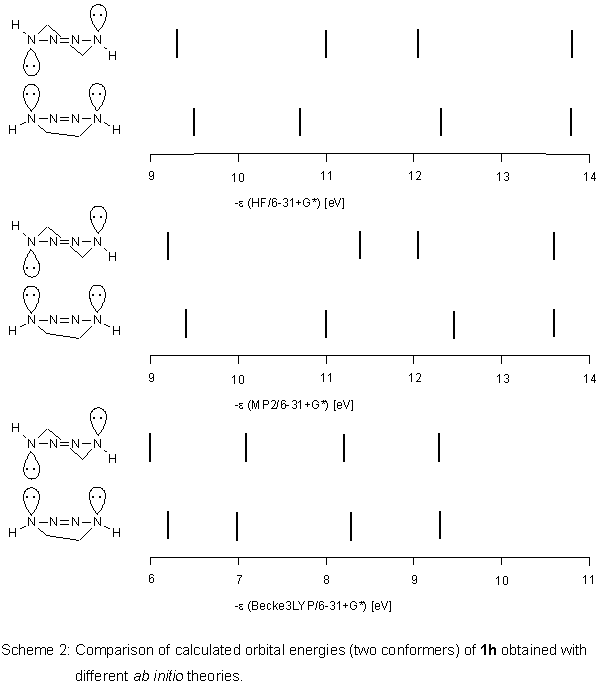This positive result was transferred to 1. According to
Becke3LYP/6-31+G*, the
two conformers of 1 are very close
in total energy, the unsymmetrical boat being more stable by 1.09
kJ mol-1. Between the conformers, there is a maximum difference
in orbital energies of about 0.2 eV (Scheme 3), correlation with
ionization potentials is good: R2 is 0.9717 (0.9987) with a slope
of the straight line of 0.9583 (1.0025) for the half-chair (boat).
Differentiation between the conformers by photoelectron spectroscopy
is not possible because the Ei values are so similar.
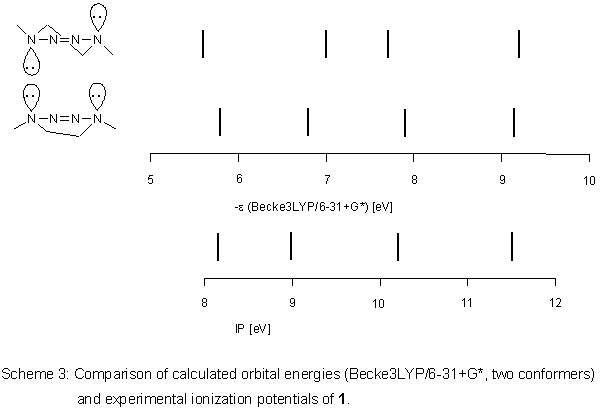The orbital sequence [2] is the same as in other cyclic 2-tetrazenes: lone pairs on N(1) and N(4) are included in a
system which leads to orbitals 3
to 1.
Lone pairs on N(2) and N(3) interact to give
n-NN and n+NN:
3 >
2 >
n-NN > n+NN >
1.
Tetrazine 2
Problems in assigning ionization bands cannot be due to different
geometrical structures because all calculations predict 2
to be planar. Rather, there is the possibility of complete conjugation
over the heteroatoms which is not taken into account properly
by semiempirical or HF ab initio methods. Becke3LYP calculations
on the other hand give orbital energies
in good agreement with ionization potentials taken from the PE spectrum (Scheme 4).
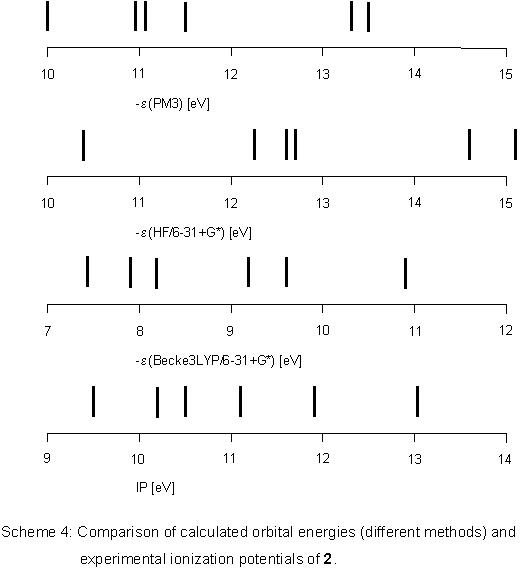In comparison to 1, the 2-tetrazene orbitals are stabilized
due to the carbonyl substitution. The lone pairs on the oxygen
atoms combine to n+O and n-O
and are included in the tetrazene orbital sequence:
3
> n+O >
2 >
n-NN > n-O > n+NN >
1.
Conclusion
Tetrazines 1 and 2 are small molecules with multiple
vicinal electron lone pairs. Semiempirical methods (PM3) reveal
difficulties in describing their molecular orbital energies correctly.
Ab initio calculations based on HF or perturbation theory
(MP2) do not perform better. Good correspondence with experimental
ionization potentials is achieved with Becke3LYP (DFT).
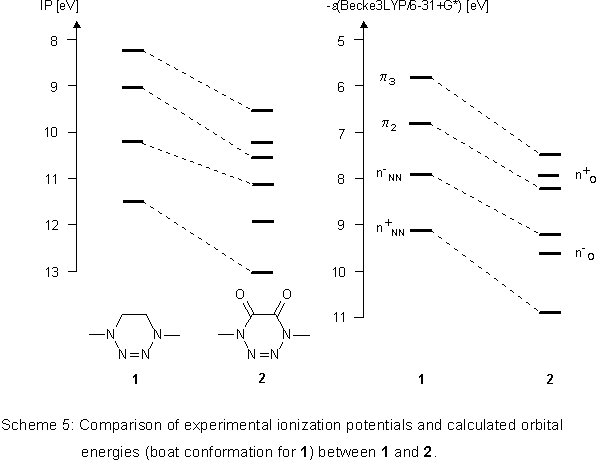
The quality of the Becke3LYP calculations can best be estimated
when both ionization potentials and orbital energies of 1
and 2 are compared with one another (Scheme 5).
References
[1] J.H.D. Eland, Photoelectron Spectroscopy, Butterworth,
London 1984; C.R. Brundle, A.D. Baker (Eds.), Electron Spectroscopy:
Theory, Techniques and Applications, 5 volumes, Academic Press,
London 1977-1984.
[2] P. Heymanns, P. Rademacher, Tetrahedron 1986,
42, 2511.
[3] S.F. Nelsen, R. Fibiger, J. Am. Chem. Soc. 1972,
94, 8497.
[4] T. Koopmans, Physica 1934, 1, 104.
[5] J.J.P. Stewart, J. Comp. Chem. 1989, 10, 209.
[6] A.D. Becke, J. Chem. Phys. 1993, 98, 5648;
C. Lee, W. Yang, R.G. Parr, Phys. Rev. B 1988, 37,
785.
