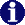To work with a particular MO pick labels first (on the right frame) and then proceed with the operations.
In this exercise symmetry properties of Molecular Orbitals are explored.
C2H4 : symmetry adapted LCAO-MO combinations for the 1s orbitals of the four equivalent hydrogens of ethylene are given. The D2 subgroup of D2h can be used to find to which irreducible representation each of the LCAO-MO "belongs" (i.e. to which irreducible representation of the group any one of the MO is a base ). A "g" (gerade or symmetric) or a "u" (ungerade or antisymmetric) subscript can be added by studying the symmetry properties of each MO with respect to inversion.
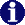To work with a particular MO pick labels first (on the right frame) and then proceed with the operations.
For this exercise you will need a character table. You should try to convince yourself that the MO's given are correct. A good starting point is to work out (pen and paper work) the reducible representation spanned by the four 1s orbitals of the Hydrogens in ethylene and then express it in terms of the irreducible representations of D2h.
Check the choice of coordinates in the character table that you are using.( Because there are three mutually perpendicular C2 axes in D2h, the choice of x,y and z is arbitrary. A relabelling of this axes will lead to an interchange of the labels B1,B2 and B3).
C2H6 staggered : similar to the previous exercise.Look at the symmetry properties of the given MO's with respect to inversion to distinguish between the Eg and Eu sets.
Back to Main Menu