Möbius bis and tris-Spiroaromatic Systems

David Hall and Henry S. Rzepa^*

Department of Chemistry, Imperial College London, SW7 2AY

Summary: We propose that a general class of bis and tris-spiro 7-membered ring systems with a common atom X, of which there are a number of examples characterised crystallographically, can in fact be considered as spiroaromatic molecules in which each ring exhibits some degree of Möbius 4np-electron aromaticity. The aromaticity is probed as a function of the spiro-atom using ab initio calculations of the NICS(0) values, which indicate that the Möbius-aromaticity increases as the spiro-atom is changed e.g. from Al to P, and from e.g. P to As.

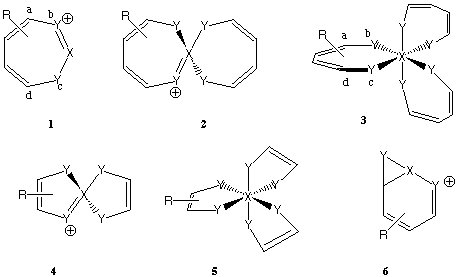
Heilbronner was the first to suggest¹ that a 180^o phase shift in the p_p-p_p overlap of a cyclic array of such orbitals, delocalised over the entire ring, would form a so-called Möbius aromatic system if the resulting closed shell p molecular orbitals were occupied by 4n electrons. Following the proposal by Schleyer and co-workers² 34 years later that the conjugated 4n p_p C₉H₉⁺ cation exhibits such aromaticity, an increasing number of diverse systems exhibiting in variable degree Möbius aromaticity have been identified.^3-7. We recently suggested⁸ potential metal ligands of the general formula 1 (Y=NR, O; X=C^-,Si^-) which as 4n p_p systems exhibit predicted geometrical distortions towards C₂ symmetry, driven by concomitant reduction of Hückel anti-aromaticity and increase in Möbius aromaticity. We subsequently argued⁷ that if the atom X is capable of 4- or higher coordination, then conjugated ring systems joined at the single atom X become possible. We used the term spiroaromatic to indicate those cases where each ring was itself capable of sustaining aromaticity, and suggested several examples where the spiro atom comprised a group V element such as phosphorus⁹ or arsenic. The analogy to the Möbius aromaticity present in the co-called coarctate transition states^10,11 was also noted. In the present article, we extend the motif of 1 to the series 1-3, where both bis and tris Möbius spiroaromaticity might be revealed. Hexacoordinated systems of type 3 in particular constitute an important class of complex involved in asymmetric two-center catalysis¹² for which Möbius aromaticity has not hitherto been previously studied or recognised.

Computational Procedure.

Molecular structures were normally optimised without symmetry constraints using Gaussian98¹³ at the closed shell B3LYP/6-31G(d) level. The aromaticity of these systems was quantified using a NICS ¹⁴ probe placed at the ring centroid. Coordinates are available via the electronic supplemental data (ESI) at http://www.rsc.org/...

Results and discussion.

A search of the Cambridge crystal database¹⁵ reveals a number of examples of the structural motifs of either 2 and 3, or the 6p (4n+2) analogues 4 and 5. The diversity includes examples of the heteroatoms Y=O, S and N and the spiro atom X spans the main group IIIB-VIB elements and the analogous transition series group IIIA-VIA. Typical (but not exhaustive) examples are shown in Table 1, for which we note that for the main group elements, the oxidation state implied by XY_n^(z-n) (z = group number) tends to be followed. In the transition series, the oxidation state of X can be lower, e.g. Cr(III) rather than Cr(VI). Amongst the closest analogues are those for 2 and particularly 3 (for which X=Al,In, P, Y, Cr(III); R=dinaphthyl). Where examples are missing we suspect it may be because of lack of synthetic incentive rather than instability. We note that in general these types of compound, and in particular the series 2 and 3 have not hitherto been analysed in terms of their potential Möbius aromaticities, which is the purpose of the current article. Here we report spiro-systems derived from main group elements, which are adequately described by single reference wavefunctions. We found that calculations on the group IIIA-VIA transition metal analogues require multi-reference wavefunctions due to the ground states having several electronic configurations of similar energy. The MCSCF convergence for such systems tend to be problematic, and currently no MCSCF-NICS procedure¹⁴ is implemented.¹³ For these reasons, calculations for the transition series are not included here.

The Dicoordinate Series 1.

We previously reported³ that for the hetero-rings 1 with X=C^-,Si^- a C₂ distortion from planarity is predicted to occur, accompanied by a reduction in the planar anti-aromaticity. Here we tabulate the analogous properties of the X=N and P series (Y=O,NH,NF, R=H, F, Table 2), which we include for comparison with the four and six coordinated analogues 2 and 3. As was previously noted for R=H, the C₂ distorted geometry is a true minimum in the potential surface, revealing no negative roots for the force constant matrix. The only exceptions are when Y=NF, for which the C₂ geometry exhibits a small imaginary normal mode corresponding to a distorsion to a lower energy bicyclic form 6.

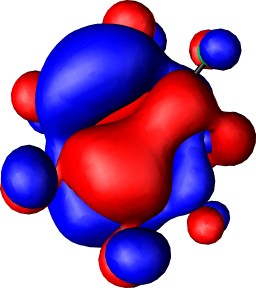
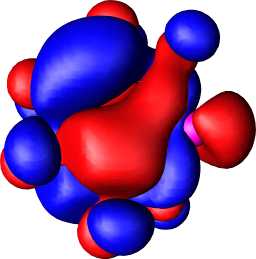
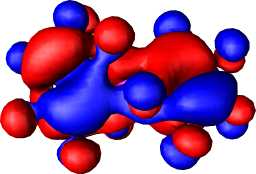
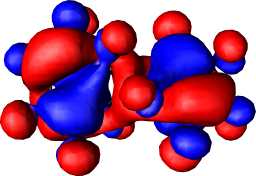
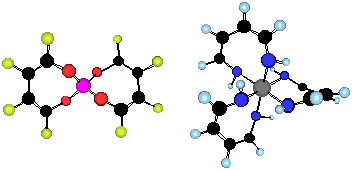
The computed (positive) NICS(0) values reveal the basic ring system 1, X=N or P to be strongly anti-aromatic, despite a moderate degree of Möbius-aromatising C₂ twisting. This anti-aromaticity is reduced (or the aromaticity increased) by replacing the ring hydrogens with fluorine, and the degree of ring twist is also increased (Table 2) by this substitution. This "Möbius-fluorine" effect appears to be stronger when Y=NF than when Y=O, but the effects of changing from X=N to X=P are small. The Möbius character can be qualitatively illustrated in the form of the highest occupied molecular orbitals (Figure 1a and b). For both X=N and X=P, the HOMO takes the form of a catenane or rotaxane-like interlinking of the two phases of the wavefunction, characteristic⁴ of Möbius aromatic rings.

The Tetracoordinate Series 2 and 4.

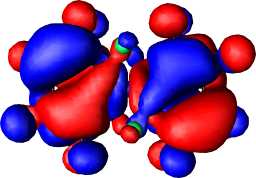
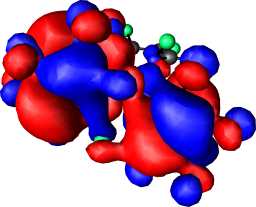
The next issue to resolve is whether the reduction of Hückel anti-aromaticity can be sustained when two heterocyclic rings 1 are spiro-fused via the central atom X, and whether the greater ability of the 2nd period elements (X=Al-P) to involve in some degree the 3d orbital shell could promote the ability of the ring to sustain Möbius aromaticity. Each individual ring again has local optimised C₂ symmetry; attempts to find other ring conformations all converged to this form. The modestly negative NICS(0) values for Y=O, NH and the high degree of ring twist indicate that even for X=N, each ring has lost the anti-aromaticity associated with planar 1. One possibility is that X=N is acting as an insulator, inhibiting p conjugation across it, and hence creating a formally non (or homo) aromatic system. The form of the molecular orbitals suggests otherwise (Figure 1). The HOMO for 2, X=N, Y=NF contains nodes for each ring essentially identical that for the single ring in 1. Using rotaxane terminology, the two orbital phases are associated respectively with the "eye" and "thread" of the needle for one ring and become reversed for the other ring (i.e. what was the eye becomes the thread, and vice versa). The HOMO reveals a node at the X=N atom, indicating little cross-ring conjugation. With X=P however an increased contribution from the P-3d orbitals indicates the HOMO and HOMO-1 for this system (Figure 1e and f) to be more strongly coupled across the rings; the HOMO shows an eye/thread:thread/eye motif for the two rings, whilst the HOMO-1 reveals a eye/thread:eye/thread nodal pattern. When fluoro substituted, each ring becomes modestly aromatic (compared to e.g. benzene which has a NICS(0) value of approximately -10 ppm) with a concomitant increase in the ring twisting.

The other noteworthy feature is that the twist of each ring can have either the same or opposite chirality, resulting in the possibility of chiral diastereomers for the overall molecule. The calculations indicate that these differ insignificantly in energy (Table 2).

Changing the 7-membered 8p (4n) ring to a five membered 6p (4n+2) system as in 4 reveals the latter ring to be entirely planar and untwisted, with NICS(0) values which indicate significant (Hückel-like) aromaticity. A similar observation of ring aromaticity was made previously by Wang and Schleyer⁹ for tetracoordinate phosphabenzene systems.

The Hexacoordinate Series 3 and 5.

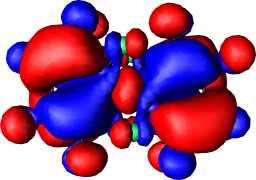
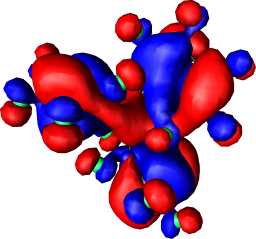
In 3, the central atom is octahedrally coordinated, and with each of the 7-membered rings being capable of a C₂ chiral distortion, two chiral diastereoisomers become possible. With X=P^- and Y=O, the parent ring appears to favour the RRS/SSR chiral isomer; the combination X=P^- and Y=NH in contrast favours the RRR/SSS form. Compared with 2, the NICS(0) value is slightly more negative (aromatic) and the degree of ring twist slightly greater, both suggesting a slight increase in Möbius character. As before, ring fluorination increases the NICS(0) value to a similar magnitude to that for benzene (~-10ppm) and again increases the degree of ring twist. By these criteria at least, these rings are now amongst the most Möbius-aromatic systems yet identified. The form of the degenerate HOMO for 3, X=P, Y=NF and HOMO-2 reveal a similar nodal pattern as previously described for 2.

We also explored variation of X to see how this might influence any Möbius characteristics. The series X=Al, Si, P reveals an increase in the negative NICS(0) values and this is also true in moving down a column, i.e. from Si to Ge, and from P to As; thus the latter system is predicted to carry the greatest degree of Möbius aromaticity of the systems studied. Finally in the hexacoordinate series, we note that the five membered 6p (4n+2) system as in 5 appears to sustain lower (Hückel) aromaticity compared to the four-coordinate analogue.

Conclusions

We have studied a series of 4- and 6-coordinate systems containing a main group atom (X) which can act as a spiroaromatic bridge across two aromatic ring systems. When these rings correspond to 8p systems, a C₂ distortion can occur to alleviate the formal planr anti-aromaticity. As components of the bisspiro rings 2, the effect is to create mildly Möbius-aromatic rings, and the aromaticity is enhanced by ring fluorination, and by the nature of X, with lower row or higher main group elements favouring aromaticity. The form of the computed molecular orbitals shows a significant degree of cross-conjugation between the spiro-rings. Examples of this type of compound are also known to occur in the transition metal series (e.g., V, Cr, etc) for which variable oxidation states add a further level of subtlty. Calculations on these systems currently present technical challenges which we anticipate will find solution in the future.

Table 1. Representative examples in the Cambridge Database exhibiting structural features of 2 - 5.^a

^aCambridge reference code and oxidation state of X as determined from the charge on the counter ions (not shown). 3D models of each structure are available via the ESI. ^b K. Ishihara, M. Miyata, K. Hattori, T. Tada and H. Yamamoto J. Am. Chem. Soc., 1994, 116, 10520. ^cT. Arai, H. Sasai, K. Yamaguchi and M. S. Hibasaki J. Am. Chem. Soc., 1998, 120, 441. ^dT. Arai, H. Sasai, K. Aoe, K. Okamura, T.Date and M. Shibasaki Angew.Chem.,Int.Ed.Engl., 1996, 35, 104. ^eS. Chitsaz and B. Neumuller Organometallics, 2001, 20, 2338. ^fS. Matsunaga, J. Das, J. Roels, E. M. Vogl, N. Amamoto, T. Iida, K.Yamaguchi and M.Shibasaki J. Am. Chem. Soc., 2000, 122, 2252. ^g R. Tacke, A. Stewart, J. Becht, C. Burschka and I.Richter, Can.J.Chem., 2000, 78, 1380. ^h R. R. Holmes, S. Shafieezad, V. Chandrasekhar, A. C. Sau, J. M. Holmes and R. A. Day J. Am. Chem. Soc., 1998, 110, 1168. ⁱH. Wunderlich, Acta Crystallogr.,Sect.B, 1981, 37, 995. ^jD. J. Sherlock, A. Chandrasekaran, T. K. Prakasha, R. O. Day and R. R. Holmes Inorg. Chem., 37, 93. ^kH. R. Allcock and E. C. Bissell J. Am. Chem. Soc., 1973, 95, 3154. ^lB. A. Borgias, G. G. Hardin and K. N. Raymond Inorg. Chem., 1986, 25, 1057. ^mJ. Wegener, K. Kirschbaum and D. M. Giolando J. Chem. Soc., Dalton Trans., 1994, 1213. ⁿG. Smith, A. N. Reddy, K. A. Byriel and C. H. L. Kennard Aust. J. Chem., 1994, 47, 1413. ^oK. von Deuten, W. Schnabel and G. Klar Cryst. Struct. Commun., 1980, 9, 161. ^pO. Lindqvist Acta Chem.Scand., 1967, 21, 1473. ^qT. Nemoto, T. Ohshima, K. Yamaguchi and M. Shibasaki J.Am.Chem.Soc., 2001, 123, 2725. ^rH. C. Aspinall, J. F. Bickley, J. L. M. Dwyer, N. Greeves, R. V. Kelly and A. Steiner Organometallics, 2000, 19, 5416. ^sTing-Bin Wen, Bei-Sheng Kang, Cheng-Yong Su, Da-Xu Wu, Li-Ge Wang, Sen Liao and Han-Qin Liu Bull.Chem.Soc.Jpn., 1998, 71, 2339. ^tB. A. Borgias, S. R. Cooper,Y. B. Koh and K. N. Raymond Inorg. Chem., 1984, 23, 1009. ^uM. Cowie and M. J. Bennett Inorg.Chem., 1976, 15, 1595. ^vBei-Sheng Kang, Xiu-Jian Wang, Cheng-Yong Su ,Han-Qin Liu, Ting-Bin Wen and Qiu-Tian Liu Transition Met.Chem., 1999, 24, 712. ^wP. R. Challen, D. H. Peapus and K. A. Magnus, Polyhedron, 1997, 16, 1447. ^xM. Cowie and M. J. Bennett, Inorg. Chem., 1976, 15, 1589. ^yR. J. Cross, L. J. Farrugia, D. R. McArthur, R. D. Peacock and D. S. C. Taylor, Inorg.Chem., 1999, 38, 5698. ^zHo-Chol Chang, S. Kitagawa, M. Kondo and T. Ishii, Mol. Cryst. Liq. Cryst. Sci. Technol.,Sect.A, 1999, 335, 183. ^aaC. Lorber, J. P. Donahue, C. A. Goddard, E. Nordlander and R. H. Holm, J. Am. Chem. Soc., 1998, 120, 8102.

^aNICS(0) value, ppm (dihedral angle a-b-c-d). ^b The designation RR/RS or RRR/RRS indicates relative rather than absolute chiral configurations for the 7-membered rings. ^c Wavenumber for imaginary normal mode corresponding to distortion to 6. ^d Dissociates to C₄F₄O₂ and C₄F₄NO₂⁺. ^e Energy (kcal/mol) relative to chiral diastereomer.

Figure 1. RHF/6-31G* computed molecular orbitals, contoured at 0.01 Hartree for (a) HOMO of 1, X=N, Y=NF, (b) HOMO of 1, X=P, Y=NF, (c) HOMO of 2, X=N, Y=NF, (d) HOMO-1 of 2, X=N, Y=NF, (e) HOMO of 2, X=P, Y=N, (f) HOMO-1 of 2, X=P, Y=NF, (g) HOMO of 3, X=P, Y=NF, (h) HOMO-1 of 3, X=P, Y=NF

(a)	(b)
(c)	(d)
(e)	(f)
(g)	(j)

References

1. E. Heilbronner, Tetrahedron Lett., 1964, 29, 1923.
2. M. Mauksch, V. Gogonea, H. Jiao and P. von R. Schleyer Angew. Chemie Int. Edition, 1998, 37, 2395.
3. C. Kastrup, S. Oldfield and H. S. Rzepa, ChemComm., 2002, 642-643; W. L. Karney, C. J. Kastrup, S. P. Oldfield and H. S. Rzepa, J. Chem. Soc., Perkin Trans 2, 2002, 388-392.
4. S. Martin-Santamaria and H S. Rzepa, ChemComm., 2000, 1089; idem, J. Chem. Soc., Perkin Transactions 2, 2000, 2372-2377
5. C. Castro, C. M. Isborn, CW. l. Karney, M. Mauksch, P. von Schleyer, Organic Letters, 2002, 4, 3431-3434. �
6. R. P. Johnson and K. J. Daoust, J. Am. Chem. Soc.,, 1996, 118, 7381-7385; R. W. A. Havenith, J. H. Van Lenthe L. W. Jenneskens, Int. J. Quant. Chem, 2001, 85, 52-60.
7. H. S. Rzepa and K. Taylor, J. Chem. Soc., Perkin Trans 2, 2002, in press
8. C. Kastrup, H. S. Rzepa and S. V Oldfield, Dalton Trans., 2002, 2421.
9. Z.-X. Wang, and P. von R. Schleyer, Helvetica Chimica Acta, 2001, 84, 1578-1600.
10. R. Herges, Angew. Chem. Int. Ed., 1994, 33, 255; C. Berger, C. Bresler, U. Dilger, D. Geunenich, R. Herges, H. Rottele and G. Schroder, idem, 1998, 37, 1850.
11. F. Hernandez Blanco, D. C. Braddock, S. Martin-Santamaria, and H. S. Rzepa, Internet J. Chem., 2001, 4, article 10.
12. M.ÊShibasaki , M.ÊKanai and K.ÊFunabashi, ChemComm, 2002, 1989-1999.
13. Gaussian 98 (Revision A.11), M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian, Inc., Pittsburgh PA, 1998.
14. P. von R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao, and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317; H. Jiao and P. von R. Schleyer, J. Phys. Org. Chem., 1998, 11, 655.
15. F. H. Allen and O. Kennard, Chemical Design Automation News, 1993, 8, pp 1 & 31-37.