An approach is presented which starts from two fundamental concepts in organic chemistry, chirality and aromaticity, and combines them into a simple rule for stating selection rules for pericyclic reactions in terms of achiral Hückel-aromatic and chiral Möbius-aromatic transition states. This is illustrated using an example which leads to apparent contradictions if treated using more conventional selection rules, but is readily understood in terms of the aromatic transition state model.
The electronic theory of organic chemistry underpins one of the most interesting, but subtle, concepts currently taught in the subject, that of the "stereoelectronic control" of reactions. For a particular mechanistic type known as the pericyclic reaction, other concepts fundamental to organic chemistry such as stereochemistry, chirality, aromaticity and quantum mechanics are interwoven. The impact of this fusion of ideas on organic chemistry has been recognized with the award of a Nobel prize in 1981 to one the original architects, Roald Hoffmann (the other, Robert Woodward, had died in 1979 and was ineligible to receive the prize posthumously). In this article, these diverse concepts are brought together via an illustration of transition states for one specific pericyclic reaction which played a key role in the first experimental synthesis of a new type of molecule, a Möbius annulene.
The discoverer of the electron itself, J. J. Thomson, was amongst the first to also develop models using the electron to account for chemical bonding. In 1921, just before the dawn of quantum mechanics, he published1 an exploration of the bonding for the archetypal aromatic molecule benzene. In his scheme, each C-C region in this species was bonded using three electrons (Figure 1, left). Reading his description, it is evident that the electron was still very much regarded as a point particle, and that there was yet hardly a glimmer of recognition that the group of three electrons might have differing spatial (3D) characteristics. The advent of quantum mechanics and the formulation of the Schroedinger wave equation brought with it an understanding of the spatial and energetic properties of electrons, more formally described by wavefunctions. This allowed a segregation of two of Thomson's three electrons in each C-C region of benzene into a low energy σ set, which form what is now called a C-C σ bond, and the third electron as contributing to a spatially distinct band of six rather higher energy electrons not directly associated with any single C-C bond but with the aromatic ring itself, and which became widely known as the aromatic π sextet (Figure 1, right).2
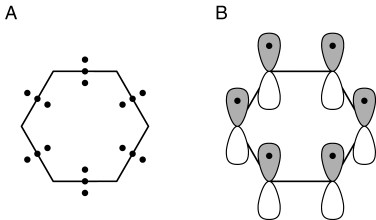
Figure 1. (left) Thomson's three electron bonds in benzene and (right) the segregation of these 18 electrons into six pairs of two electron C-C bonds and a π aromatic sextet following Hückel.
The first person to formalize this separation was Erich Hückel in 1930.3 He used the new theory of quantum mechanics to derive a principle of σ/π separability, which he used to explain the restricted rotation in alkenes. Hückel in 1931 extended this concept to benzene itself, predicting particular stability for a cyclic arrangement of six π electrons in wavefunctions (Molecular Orbitals) formed by overlapping carbon-centered 2p atomic orbitals into a planar ring. The concept of atomic orbitals themselves had previously been derived by solving the quantum mechanical Schroedinger wave equation for a hydrogen atom. It took little while longer for organic chemists to properly generalize and understand Hückel theory as a useful, albeit approximate theoretical basis for the wider concept of aromaticity. The emergent Hückel rule (first succinctly coined not by Hückel himself but by William Doering as late as 19513), is conventionally applied to planar molecules containing cyclically conjugated π electrons (referred to below as having Hückel topology) and is now enumerated as the following;
Rules 2 and 4 were added in the 1960s, as the quantum mechanical understanding of photochemically excited states (open shell systems with two molecular orbitals each singly occupied) developed. These nowadays are regarded as a much more approximate heuristics than the thermal rules 1 and 3.
A particularly characteristic feature of what might be called "classical" aromatic chemistry is the planarity (two-dimensionality) of the ring. When the representation of a planar molecule is reflected in a mirror, the three dimensional arrangement of atoms can be exactly superimposed on the original unreflected set; such molecules are said to be achiral. A small class of aromatic molecules are forced to be non-planar for steric reasons. A good example are the helicenes, which adopt a helical arrangement of the rings (Figure 2). When reflected in a mirror plane, such a helicene cannot be superimposed upon the original and the system is said to exist as a pair of chiral or disymmetric enantiomers. Of course, aromatic molecules can support chiral groups as substituents on the rings, but we exclude this class in our argument here, since we are concerned only with the nature of the aromatic structures themselves.
Figure 2. A heptahelicene and its non-superimposable mirror image.
Thus these two great concepts of organic chemistry, aromaticity and chirality, remained mostly exclusive. Edgar Heilbronner in 19644 and Howard Zimmerman in 19665 both came up with radical new suggestions which allow a fusion of these concepts. Rather than distributing π electrons in a planar ring comprising precisely parallel overlap of 2p atomic orbitals, Heilbronner considered what might happen if this array were instead distributed along a Möbius strip bearing a single half (left or right) twist (Figure 3).
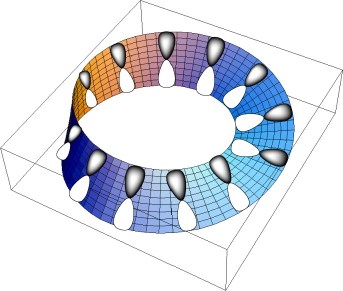
Figure 3. Heilbronner's suggestion for a π-Möbius conjugated system obtained by π electrons located in molecular orbitals resulting from 2p atomic orbitals distributed around a Möbius strip bearing a single half-twist, rather than a planar Hückel ring bearing no twist in the orbital basis.
Heilbronner applied Hückel 's equations3 to such a cyclic Möbius ring, finding that a 4n π electron system would be a closed shell species like benzene, with no loss of π-electron resonance energy compared to the equivalent untwisted Hückel ring. A closed shell 4n+2 π electron Möbius ring was predicted to be less stable than the untwisted Hückel counterpart.
Like Hückel before him, Heilbronner did not derive a succinct rule of aromatic stability from these results. Zimmerman5 was the first to clearly associate the π-electron stability of such Möbius rings with an inversion of the aromaticity rules 1 and 2 above. Specifically, populations of 4n π electrons result in closed shell (two electrons per π energy level) molecules if the 2p atomic orbitals are distributed along a Möbius strip (rule 1 inverted), whereas 4n+2 π-electrons will adopt an open shell (photochemical) distribution in which two of the electrons will now each occupy a separate molecular orbital (rule 2 inverted).5 By adding a corollary for the anti-aromatic cases, rules 5-8 to complement 1-4 can be listed;
A useful visual mnemonic first proposed by Frost and Musulin6 for orbital energies of π-electron rings based on inscribing a polygon with one vertex down for the Hückel rules, was memorably extended by Zimmerman5 to Möbius systems by redrawing the polygons with one edge down (Figure 4).
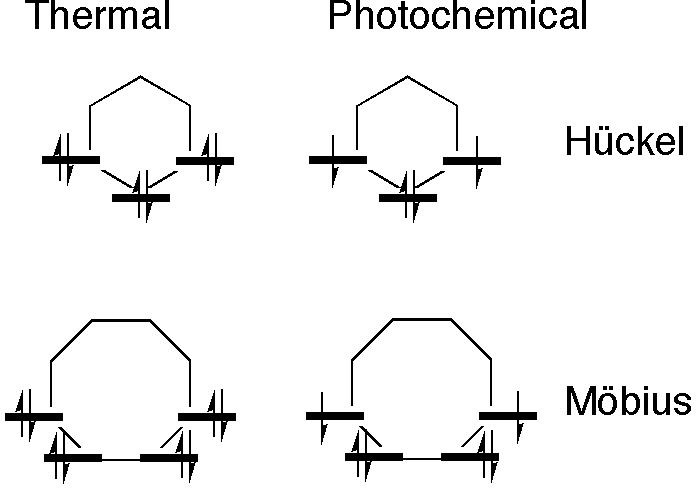
Figure 4. Frost-Musulin/Zimmerman mnemonics for aromaticity selection rules. A six sided polygon is shown for the Hückel case to coincide with the example shown later in Scheme III (red arrows) and an eight-side polygon is shown for the Möbius case to coincide with the blue arrows in Scheme III.
Another aspect of Möbius systems which was not directly commented upon by Heilbronner is that a Möbius strip bearing one half-twist is also chiral, in the sense noted above for the heptahelicene molecule (Figure 2). An ideal Möbius strip has only a C2 axis of symmetry present. The specific absence of a plane of symmetry means the mirror image of a Möbius strip is not superimposable upon the original. In contrast, an ideal planar aromatic molecule of the Hückel type does have at least one plane of symmetry, referred to here as a Cs mirror plane, which means that its mirror image is superimposable with the original. Thus in Möbius ringed molecules, we do now have a fusion of two seminal concepts in organic chemistry, that of aromaticity and of chirality!
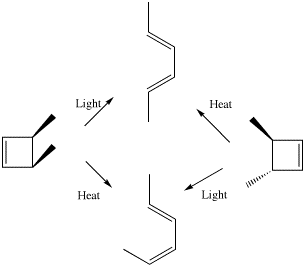
Scheme 1. An example from Woodward and Hoffmann illustrating how the outcome of a pericyclic reaction depends on stereoelectronic control mediated by heat or by light.
The next intellectual leap involves a class of organic reaction known as pericyclic, and the recognition by Woodward and Hoffmann7 that the stereochemical outcome of such reactions was quantum mechanical in origin (Scheme 1). The original Woodward and Hoffmann argument was based on the symmetries of a subset of the molecular orbitals called frontier orbitals. This analysis was extended by Longuet-Higgins and Abrahamson7 to a more formal diagram showing the correlation of the symmetries of the reactants and product molecular orbitals, and particularly whether either of the C2 or the Cs symmetry elements noted above were preserved during the course of the pericyclic reaction. A difficulty in applying such symmetry arguments was the experimental observation that most pericyclic reactions involved no formal symmetry at all! This difficulty can be overcome by the following procedure.
The first person to associate the π-electron stability (aromaticity) of Möbius and Hückel rings with the "allowed" or "forbidden" nature of the transition states for pericyclic reactions was Zimmerman,5 via the mnemonic shown above (Figure 4). Thus the preferred outcome of a pericyclic reaction can be predicted by analyzing whether the transition state might exhibit Hückel or Möbius aromaticity.7 This simple statement carries some of the most profound and powerful concepts in modern organic chemistry.
Before introducing a pericyclic reaction which can be used to embody and illustrate these concepts, one more tool is needed. How does one quantify, or measure, the concept known as "aromaticity". Although much of the discussion above is couched in terms of the (theoretical) π-electron energy, it turns out that accurate measures of aromaticity in terms of (theoretical or experimental) energies are frustratingly elusive. Many other criteria have been proposed, and the consensus seems to be that that no single experimental measurement or theoretical calculation can fully, accurately and uniquely represent aromaticity. It is also evident that experimentally measuring aromaticity for a transition state will be particularly difficult given its very short lifetime (≈ 10-15s)! Instead, recourse has to be taken to a quantum mechanical calculation rather than direct measurement. Instead of using energies, two other property calculations are used here for this purpose.
The example we have chosen is derived from a remarkable recent synthesis inspired by Heilbronner's 1964 proposal. From rule 5 above, one can see that a 4n cyclic aromatic (or annulene) is predicted to be Möbius aromatic. Herges9 and colleagues Ajami, Oeckler, and Simon set out to synthesize a [16] Möbius annulene (n=4) in the laboratory, with the purpose of subjecting it to experimental tests to see if it really were aromatic. The synthetic route is set out in Scheme II, and involves a series of consecutive pericyclic reactions. Herges was able to isolate the intermediates labeled E in this scheme, and these when subjected to light formed a mixture from which was isolated one specific product. X-ray crystallography showed that this isomer had the C2 axis of symmetry required of a Möbius annulene.
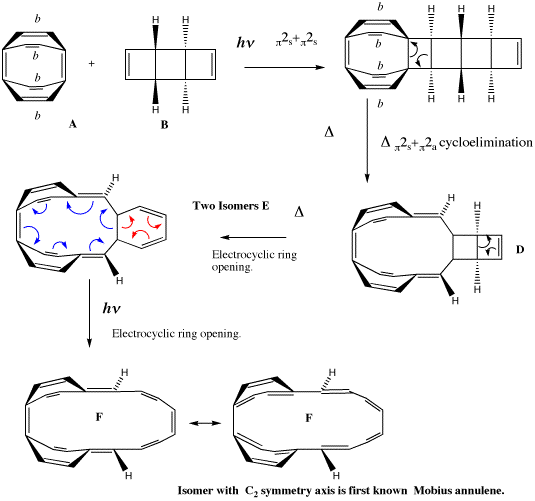
Scheme II. Herges' scheme for the synthesis of a [16] Möbius ring. Bonds marked with b carry a benzo substituent, omitted here for clarity. Isomer F with a C2 symmetry axis is the first known Möbius annulene. Note the either the red or blue arrows are used in E to form the resonance structures of F.
This synthesis was set as an undergraduate problem class associated with a course on pericyclic reaction given by the present author, and the students were invited to "push arrows" illustrating the mechanism, the total number arrows for each step then being used to derive which of the 4n/4n+2 rules listed above is applicable for that step. One characteristic feature of pericyclic problems is that often, two or more alternatives to the arrow pushing can be proposed, and normally these alternatives all result in the same analysis of the overall reaction step. So although it was no surprise that the majority of students in the class illustrated step E to F with the arrows shown in red (examples of such reactions were contained in the lecture notes for the course), a significant number of students instead chose to use the arrows shown in blue for this step. The stereochemistry at the bicyclic ring junction in E had been left undefined in the question, in the hope of provoking the students (and the present author!) to think about the implications.
A tutorial, in which this problem and possible answers to it were discussed with students, soon revealed that those students who had invoked the red arrows were led to analyzing the consequences of a 4n+2 rule (n=1), whilst those who had used the blue arrows were obliged to use the 4n rule (n=3) for this electrocyclic ring opening reaction. It seemed that for either route, one could regard the reaction as simultaneously following one rule and breaking the other, and that a contradiction seemed to exist. This certainly led to a lively tutorial.
Further thought reveals that this specific example can be used to concisely encapsulate many of the concepts required to fully understand pericyclic reactions. To illustrate these, a reasonably accurate quantum mechanical model of the two possible transition states for this reaction was computed, and is analyzed in detail below. Several simplifications of the system was undertaken to enable a practical model to be constructed.
Two transition states were located for the ring opening reaction. This was done at a level of theory summarized as B3LYP/6-31G(d), which means use of a density functional procedure with an orbital basis set for the atoms known as 6-31G(d). This combination is frequently employed nowadays and its properties are well understood.
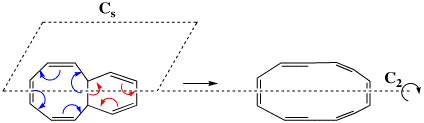
Scheme III. A simplified model electrocyclic reaction, showing the plane (Cs) or axis (C2) of symmetry which can be preserved during reaction. Note the either the red or blue arrows are used to open the ring.
The first transition state in fact corresponds to the three red arrows, maps to the 4n+2 rule, and hence is deemed to correspond to a Hückel type in which a plane of symmetry (Cs) is maintained throughout the reaction. This implies that the six-membered ring formed by the transition state is Hückel aromatic (rule 1 above). The second transition state corresponds to the four blue arrows, maps to the 4n rule, and implies that the eight-membered transition ring has C2 symmetry and is Möbius aromatic (rule 5 above). Are these properties are reflected in the two quantitative measures of aromaticity described above?
|
Cs:
Activation barrier from reactant: 29.6 |
C2:
Activation barrier from reactant: 17.9 |
|---|---|
Figure 5. Geometries and transition normal modes for electrocyclic ring opening shown in Scheme III for transition states with Cs and with C2 symmetry. The latter shows the same helical features as previously illustrated in Figure 2. Java must be installed on your system to view the animated transition states.
Shown in Figure 5 are 3D models visualized using the Jmol applet11 illustrating the calculated geometries of the two transition states. The model is animated to illustrate the form of the reaction mode. This is computed from a full vibrational analysis of the system, and shows in each case the central C-C bond periodically breaking or making, in one direction leading to the monocyclic [12] annulene, and in the other direction to the bicyclic starting material. Various properties of these transition states will be discussed individually.
These various measures of aromaticity clearly illustrate how the concept can be applied to transition states for pericyclic reaction. It also enables one to reconcile how a reaction can apparently both follow one rule, but break the other in this hybrid electrocyclic reaction. The answer is that only one ring is aromatic in each case, whilst the other ring essentially just spectates as a non-aromatic participant. In effect, stabilization due to cyclic π conjugation occurs only in the aromatic ring, whilst the spectating ring retains conventional unconjugated bonds.
The reaction shown in Scheme III illustrated how the stereochemistry at the ring junction (cis or trans) determines which of the two differently sized rings becomes aromatic in the reaction transition state. In effect, the stereochemistry defines whether the electrons represented by the blue or the red arrows are the more appropriate for the pericyclic outcome. But what if the two rings are the same (Scheme IV)?
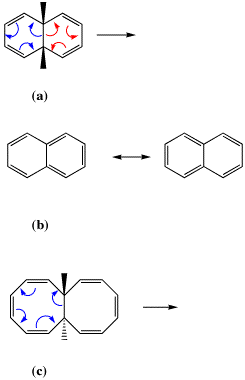
Scheme IV. Pericyclic reactions involving two identical six-membered rings (a), compared to naphthalene (b) and for eight-membered rings (c).
In Scheme IVa for example, the outcome of the blue or red arrow pushing is predicted to be identical. What does that imply about the aromaticity of the pericyclic transition state rings? Recourse can be sought to an analogy with naphthalene (Scheme 6b). This species is known to be symmetrical, which implies an electronic structure which can be represented by equally probable contributions from the two valence forms shown (along with others). Such equal resonance contribution is thought of as implying that both rings in naphthalene are equally aromatic, but that aromaticity is also associated with the larger 10-membered ring rather than just the two 6-membered rings. Since the two resonance forms in 6b are equivalent to the red and blue arrows shown for the reaction 6a, such an analogy leads us to conclude that both the 6-membered rings will be equally (and Hückel) aromatic in the pericyclic transition state for ring opening. Similarly for the 8-membered case as in 6c, the two transition state rings should also be equally Möbius aromatic. These hypotheses can be tested using the same computational procedure as described above.
|
B3LYP Method
NICS(0) -12.1, -12.1 ppm |
KMLYP Method
NICS(0) -16.6, -10.2 |
|---|---|
Figure 6. Calculated (B3LYP/6-31G(d) or KMLYP/6-31G(d)) Geometries and transition normal vibrational modes for the electrocyclic ring opening shown in Scheme IV (a).
|
(a) B3LYP Method, no symmetry NICS(0) -9.6, 1.3 ppm |
(b) KMLYP Method no symmetry NICS(0) -10.7, 0.0 ppm |
|---|---|
| B3LYP Method, C2 symmetry, NICS(0) -10.8, -2.0 | |
|
(c)
First imaginary frequency: 312i |
(d)
Second imaginary frequency: 35i |
Figure 7. Calculated (B3LYP/6-31G(d) or KMLYP/6-31G(d)) Geometries and transition normal modes for the electrocyclic ring opening shown in Scheme IV(c).
A new phenomenon is clearly manifesting here, whereby the aromaticity tends to localize in a single transition ring, rather than distributing equally across the two rings. Such an effect was first noted for stable molecules by Clar, who suggested that in polybenzenoid planar aromatic molecules, the most probable valence bond resonance forms were those that localized as many aromatic sextets as possible.13 The above example might be the first example of the "Clar effect" applied to aromatic transition states, but before so concluding, a check on whether it may instead just be an artifact of our theoretical model must be made.
There is indeed a finger of suspicion pointing at the B3LYP method used. A number of people have suggested14 that for larger rings containing 10π or more conjugated electrons, B3LYP can overemphasize the degree of bond length equality, and hence underestimate any "Clar" effect. An alternative density functional method known as KMLYP15 is thought to be more reliable in this regard. The results of using this procedure to build our models are shown in Figures 6 and 7.
The KMLYP model (with ten participating electrons) therefore shows one ring to be rather more aromatic than the other, whilst with 14 participating electrons this imbalance is fully tipped over into non-aromaticity for one ring. The smaller system could be said to be "on the edge of chaos".14c It is important to realize this effect is not due to the stereochemistry of the systems, or indeed their Möbius/Hückel nature, but to the "Clar" effect, which tends to promote clusters of smaller aromatic rings rather than delocalization on a larger scale, and which can be quite challenging to model computationally.
Chemical reactivity is a complex process, controlled by a variety of influences. Pericyclic reactions are a class which also often exhibit highly stereospecific behavior, and which are now understood to be subject to quite clear stereoelectronic influences. These in turn can be traced back to quite simple derivations of the Schroedinger wave equation, and related to another concept known as aromaticity. To do so fully, requires an understanding of selection rules expressed in terms of two different forms of aromatic species, the ubiquitous planar Hückel aromatic, and the relatively new type of Möbius-aromatic. In illustrating the first synthesis of such a stable Möbius system, we uncover one step in the sequence where the mechanism can be explained in terms of either Hückel or of Möbius aromaticity of the transition state for the reaction. This exposes a very rare example of a pericyclic reaction which at first sight appears to simultaneously obey one selection rule, and to disobey another. Reconciling this apparent discrepancy requires a deeper understanding of how aromaticity as a concept can be applied to such reactions.