The Berry pseudorotation is a classical mechanism for interchanging axial and equatorial ligands in molecules with trigonal bipyramidal geometry. It presents particular pedagogic problems due to both its dynamic and its three dimensional character. We present here an approach to illustrating such processes, which overcomes limitations of the printed page by using interactive animations. These were created using the opensource Jmol Java applet as a component of a scripted Web page, and are based on density functional (B3LYP/6-31G[3d] or B3LYP/TZVP) molecular orbital calculations applied to seven molecules; PF5, IF5 SF4, ClF3, SF4Cl2, IF7 and Sn(amidinate)2. Our calculations hold some surprises which uniquely emerge from this visual/dynamic treatment. IF5 shows fluxional behavior with characteristics of Berry and two other modes; one termed turnstile rotation and the other, a lever mechanism. In recognition of the mixed character of this exchange mechanism, we christen this a "chimeric pseudorotation". The "pure" forms of the three mechanisms are illustrated with PF5 for the Berry pseudorotation, SF4 that has a known lever mechanism as one of the pathways for terminal atom exchange, ClF3 that also exchanges terminal atoms via a lever mechanism, and with SF4Cl2 that has been shown computationally to undergo a cis/trans isomerization via a turnstile rotation. Apical/equatorial exchange in IF7, first analysed by Bartell, shows fluxional behavior of mixed character, similar to that observed for IF5. We conclude by animating the fluxional behavior of a simple model for a chiral metal catalyst Sn(amidinate)2, in which axial/equatorial exchange within the amidinate rings occurs via a Berry pseudorotation resulting in interconversion of the enantiomers.
In XY5 trigonal bipyramidal molecules with D3h symmetry (PF5, VF5, Fe(CO)5, etc), the mechanism of the exchange of the axial and equatorial terminal groups has been the source of great interest for some fifty years now, making its way into many textbooks, but not entirely without pedagogic confusion. Although, several possible mechanisms had been proposed for this fluxional behavior of XY5 molecules,1-3 examination of physical and spectroscopic data4 indicated that exchange occurred in a pairwise-fashion, with two axial atoms exchanging with two equatorial atoms in a process which did not involve any bond breaking or bond reforming (although exchange mechanisms in condensed phases that involve bond breaking and bond reforming are well known5).
The now accepted mechanism was indeed correctly, albeit briefly, described by Berry in 1960,1 and has become famously known as the Berry pseudorotation (BPR). The isomerization of trigonal bipyramidal systems was subsequently and rigorously formalised using Petersen graphs.6 In the BPR, as described by chemists, the angle (initially 120°) between one set of any two equatorial atoms in a trigonal bipyramidal molecule (A, Figure 1) increases at the same rate as the angle (initially 180°) between the two axial atoms decreases. At the maximum in the potential energy curve (the transition state, Figure 1), the four atoms in question become equivalent, and the symmetry of the molecule changes to C4v. Progressing further along the reaction pathway, the angle between the atoms that were originally axial continues to decrease and the angle between the atoms that were originally equatorial continues to increase, until the once axial atoms are now in equatorial positions and the once equatorial atoms are now in axial positions (B in Figure 1). This motion of four atoms involves only bending about the fifth central atom and no rotational components, although a simple rotation of the entire molecule by 90o would appear to take A to B, hence the term pseudorotation. In another famous article, Ugi et al3 argued that in some systems where BPR invariably leads to disfavored isomers, an alternative mechanism they named turnstile rotation (TR), might instead be preferred. Although we could find no clear cut examples of a pure TR process for unconstrained XY5 molecules, the possibility of both BPR and TR is discussed in pedagogic articles describing this type of fluxional behaviour7.
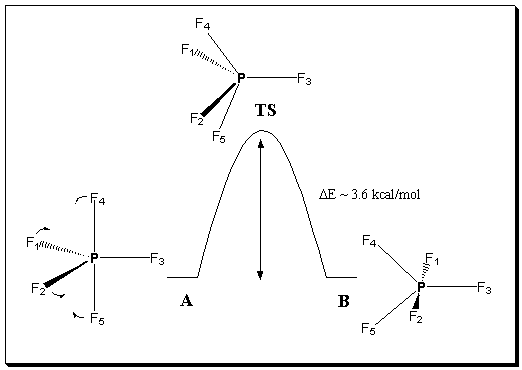
Figure 1. Potential energy diagram for the transposition of axial (atoms 4 and 5 in A) and equatorial atoms (1 and 2 in A) via a transition state in which 1,2,4,5 are all equivalent.
Our examination of several recent text-book descriptions of the Berry pseudorotation found them to be surprisingly confusing. Two different texts describe the axial/equatorial exchange in XY5 as involving a C4v symmetric intermediate or isomer (sic)8,9 and in one text the 2-dimensional representation of the mechanism would suggest it is a two-step process, first opening the angle between the equatorial atoms, and then closing down the angle between the once axial atoms.8 We suggest that a more precise description of the exchange would be to replace the term intermediate or isomer by transition state,3 in which the motion of the atoms at this geometry is best described by the normal vibrational reaction mode on the potential energy path connecting reactants and products.
We have also argued10 that in the Internet age, presenting a pedagogic interpretation of such processes should not be bound by the limitations of the printed page, whether in research journal or text book. Here we present an alternative more dynamic approach to teaching the Berry pseudorotation mechanism, together with an exploration of two other fluxional processes; the "chimeric" pseudorotation for fluxional behavior in square pyramidal molecules (using IF5 as an example) and the relatively unknown Bartell mechanism11 for the exchange of apical and equatorial atoms in the pentagonal bipyramidal molecule IF7. Neither of these latter examples appears to have been previously discussed in a pedagogic context, and both molecules appear to have surprising features with respect to apical/equatorial atom exchange. Both the "chimeric" and the Bartell mechanism show behavior characteristic of a "lever" mechanism, the "turnstile" mechanism and the Berry mechanism. To illustrate simple examples of the lever mechanism and the turnstile mechanism, we have animated the fluxional processes for SF4 which exhibits one pure lever mode (in addition to one lower energy Berry pathway), for ClF3 that also exhibits a pure lever pathway, and for SF4Cl2 which has been shown computationally to interconvert cis/trans isomers via a turnstile mechanism.
Our first example illustrates the PF5 molecule, since it is the quintessential example used in texts, has well known ground and transition state structures, and is a small molecule constructed from atoms for which high quality basis sets for computation exist. In a recent article, Montgomery7 discusses the possibility of both BPR and TR mechanisms for this system, but draws conclusions based on relatively low level energy calculations, and without the formal location of transition state structures. We present here an approach to studying the mechanism using visualisation tools, with animations based on formal calculation of the transition state and its vibrational modes using reasonably high level modern density functional-based molecular orbital theory.
The D3h ground state structure of PF5 is very well predicted at the B3LYP/6-31G(3d) level (The B3LYP calculation, a variant of density functional theory, was used in combination with a set of atomic basis functions describing each atom known as 6-31G(3d)).12 We next assumed that a square pyramidal initial geometry of C4v symmetry might form a good initial guess for a possible transition state structure for interconverting a pair of axial and equatorial fluorines. The geometry of this species was optimised by invoking a transition state locating algorithm which inter alia ensures that all the first derivatives of the calculated energy with respect to the nuclear coordinates are zero. To show that this does indeed result in the location of a transition state, the second derivative matrix (of energy with respect to coordinates, also called a Hessian matrix) was calculated and diagonalised. A true transition state will have one negative root representing an imaginary frequency ( which is an eigenvalue, also called a force constant) for this matrix, although at this stage we do not yet know if it is the transition state which connects our desired reactants and products on the potential energy surface. The process of matrix diagonalization also associates a set of displacement eigenvectors with each eigenvalue of the matrix, including one set corresponding to the single negative root. Displacing the nuclear coordinates along these particular vectors (in a harmonic approximation, the displacement is the same whether the vectors are all pre-multiplied by either +1 or -1) will necessarily lower the energy of the molecule. Following either the positive or the negative displacement along the potential surface would eventually lead to either the reactant or the product of the reaction. In case of PF5 of course, if the correct transition state has been found, the reactant and product would be identical, but with two axial and two equatorial ligands transposed.
Examination of this normal mode for the C4v transition state (Figure 2) is best achieved by animation, and we used the program Jmol13 to achieve this. The magnitude of the displacement vectors has no absolute physical significance (they are normalised so that the sum of all the squared displacements equals 1), but equating their numerical value with Angstroms turns out to be fairly similar to the actual vibrational motions of the atoms. At the resulting points of maximum displacement from the transition state, the geometries emerge as being essentially identical to the ground state structures (Figure 2, structures A and B). Examination of this vibrational mode also clearly demonstrates oscillation between the two forms and axial/equatorial exchange in pairwise fashion as described in a Berry pseudorotation and hence the vibration clearly lies on potential energy surface linking the two ground states. This established beyond doubt that the C4v transition state is indeed the correct one for this process.
Two orientations of the ground state structure are shown to the left and to the right of the calculated transition state structure in Figure 2 A and B respectively. The calculated transition state structure is displayed in the center frame of Figure 2. Any of the three structures may be moved with the mouse, one of many features of the Jmol program. Tools which enhance visualization as well display the vibrational modes of the molecule were created using "buttons" with scripts from Jmol. As you can see in Figure 2, we have scripted buttons to color code the atoms, label the atoms, turn the vibrational mode on or off, add vectors, etc, and students may choose from these selections to enhance their ability to visualize the desired message in our pedagogy. Ultimately, in this example, we hope that by viewing each orientation of the ground state, turning the vibration on and then off, and then carrying out one oscillation of the vibration, from the first point in maximum displacement to the second point of maximum displacement, that students can see that one oscillation essentially steps the molecule along the potential energy curve from one ground state, through the transition state to the to the next ground state. This motion, from one ground state structure (A) to the second (B) going through the transition state is one Berry pseudorotation. PF5 is a wonderful example with which to illustrate the BPR. In part this is because the relatively low energy barrier for the process of 3.6 kcal/mol in our calculation (c.f. a value of 3.7 kcal/mol previously reported14) means that the displacement of the atoms away from the transition state along a purely harmonic normal mode in fact nicely approximates the potential energy surface linking the two equilibrium species and the transition state.

Figure 2. Interactive diagrams illustrating the pseudorotation process for PF5, and generated using the Jmol applet. Click on the thumbnail above to activate the diagram. Ensure beforehand that you have Java installed on your computer. This can be obtained from the following location: http://java.sun.com/j2se/.
The IF5 molecule represents an interesting inversion of the geometry of PF5. The square pyramidal C4v symmetric shape for the equilibrium state of IF515 (Figure 3, Structures A and B) is actually the structure of the transition state for PF5 (Figure 2). There are other differences. The barrier for intramolecular axial(apical)/equatorial exchange in PF5 is small, whereas for IF5 (and also in BrF5 and ClF5) it is thought to be substantial.16 Thus the 19F NMR spectrum of this species shows two distinct lines at room temperature in the integral ratio of 1:4, with mutual coupling, indicative of a significant barrier.16 Rather surprisingly, these differences from e.g. PF5 have been little commented upon; we have found no educational articles that discuss the nature of the exchange mechanism and the magnitude of the barrier in IF5 for example, although the graph-theoretical aspects of such systems have been described.6b
The equilibrium structure of IF5 was calculated at the B3LYP/TZVP level (TZVP, or triple-zeta-valence-polarization is a similar, indeed rather better, basis set to 6-31G[3d]), and is shown in Figure 3 as Structure A and in a second orientation in Structure B. The transition state geometry for exchange of the apical F with one of the four equatorial groups is illustrated, and the transition mode vibration animated, in the center frame of Figure 3. This transition state has only a plane (Cs) of symmetry, and is reached by a barrier of 26.7 kcal/mol from the equilibrium geometry, which is indeed substantial (that for ClF5 is calculated to be even greater).17 The transition state vibration also has a substantial associated wavenumber of 151i cm-1. Slowly stepping from one maximum (which is close in geometry to the calculated ground state structure A) in the vibrational mode through the transition state, and on to the second maximum in the vibrational mode (again close in geometry to the ground state structure B) clearly illustrates how the mechanism interchanges apical and equatorial atoms. Unlike the Berry PF5 mechanism, where two pairs of fluorines are involved in the process whilst both the P and the fifth F remain static, for IF5, all five fluorine atoms and the iodine more or less equally participate in the IF5 exchange. Three separate views of this mode (Figure 3) show how it has characteristics of a turnstile mechanism, a lever mechanism and the Berry-like bending motions. In recognition of this, we christen this mode the "chimeric pseudorotation". Chimeric stems from Chimera, the mythological Greek demon of the mixed and "monstrous" character of a goat, snake and lion. Recently, chimeric has become "a byword for fabulous and fantastic - but utterly mixed-up - ideas".18 We also retain the use of the descriptive term "pseudorotation", as it would appear that the two ground state structures are related by a simple rotation of the entire molecule (in this case by a rotation of approximately 45o).
Figure 3. Interactive diagrams illustrating the chimeric pseudorotation process for IF5, and generated using the Jmol applet. Click on the thumbnail above to activate the diagram. The transition mode for exchange of apical and equatorial F atoms in IF5 is shown, in which atom F(1) is apical in reactant, atom F(2) becomes apical in the product, and F(1) and F(2) are symmetrically equivalent at the transition state. The plane of symmetry passes through the I and F(5) atoms. The vectors shown are the (mass weighted) displacements for the transition normal mode. The vector for the iodine is rather smaller because of the greater mass of this atom. View 3 shows that the angle at F(1)-I-F(3) is opening whilst that at F(2)-I-F(4) is closing (Berry pseudorotation). A different view (View 1) showing how atoms F(1), F(2) and F(5) are rotating clockwise, whilst F(3) and F(4) are rotating anti-clockwise (Turnstile rotation). View 2 shows "lever-like" character reminiscent to that calculated for SF4 shown in Figure 4b below.
In the context that IF5 shows some "lever-like" character in the mechanism that exchanges apical and equatorial terminal atoms, we illustrate the pure "lever mechanism" that has been proposed19 as one of the two mechanisms for terminal atom interchange in SF4 and related AX4 systems. The equilibrium shape for such systems (which have C2v symmetry, illustrated in Figure 4a and/or 4b) has been given many names; distorted tetrahedron, see-saw, truncated trigonal bipyramidal, truncated square pyramidal, and disphenoidal. The "lever" transition mode was reported as retaining only a plane of symmetry (Cs) and to co-exist with, but to be about 10 kcal/mol higher in energy than, a second transition mode corresponding to true Berry pseudorotation. Because no animated diagrams illustrating the "lever" mechanism were included with the original report19, we have repeated those calculations here. Comparing the animated "lever" mode (See Figure 4b) for SF4 with our chimeric pseudorotational mode for IF5 allows one to clearly perceive the similarity between these two modes; the difference being that one of the basal fluorines in IF5 is replaced by a lone pair in SF4. Although we have used SF4 as our example to illustrate a lever mechanism, note that Berry pseudorotation is the lower energy pathway for axial/equatorial exchange in SF4 and certain other reported disphenoidal molecules.19,20 We have therefore also presented animations of the BPR for SF4 (See Figure 4a).


Figure 4. Interactive diagrams illustrating the fluxional processes for SF4, ClF3 and SF4Cl2, and generated using the Jmol applet. Click on the thumbnails above to activate the interactive diagrams. Illustrated are (a) The conventional Berry pseudorotation for SF4, (b) the less conventional "lever" mechanism for SF4, (c) the lever mechanism for ClF3 and (d) the turnstile rotation in SF4Cl2.
A simplier example of the lever mechanism is animated in Figure 4c. ClF3 has an equilbrium geometry described in VSEPR terminology as T-Shaped, with two terminal F atoms occupying axial positions, and one terminal F atom and the two lone electron pairs in equatorial positions. Apical(axial)/equatorial atom exchange occurs through a lever mechanism for this molecule.21
The next animation that we present came from our search for a molecule that might interchange axial (or apical) and equatorial atoms via the elusive turnstile mechanism noted in our introduction. Although Ugi et al3 proposed early on that some trigonal bipyramidal molecules might interchange axial and equatorial atoms using a turnstile mechanism, we had hitherto found no known examples of molecules with D3h symmetry that undergo this type of exchange via a pure turnstile mechanism. The dynamic processes that interchange coordination sites in some six coordinate organometallic compounds have been observed to involve an intramolecular non-dissociative turnstile mechanism in competition with dissociative ligand exchange mechanisms22, one calculational study indicates that a turnstile rotation leads to isomerization in some Pd(II)L5 complexes23, and one experimental study proposes that a turnstile rotation is responsible for intramolecular exchange in the square pyramidal intermediate found in the isomerization of a square planar Pd(II) complex.24 Octahedral molecules such as SF6 can also undergo a TR-like twisting motion of three F atoms with respect to the other three that interchanges the positions of the terminal atoms, but since all the terminal atoms in this particular system are symmetry equivalent to begin with, there is no simple way to detect this process experimentally. However, the mixed halogen system SF4Cl2, which rather curiously is an unknown molecule, can have either a cis or a trans relationship of the two Cl atoms. To illustrate how a turnstile rotation would in principle interconvert such isomers, we include the calculated transition state and animation for this process in Figure 4d. The computed barrier for this process of 65 kcal/mol is remarkably large.
The pentagonal bipyramidal IF7 molecule with D5h symmetry25 proved equally interesting. B3LYP/TZVP calculations reveal surprising aspects of the transition state vibrational normal mode (Figure 5). The process was first suggested by Bartell11 and serves to interchange one set of two equatorial atoms with the two apical atoms. The barrier for this process we calculate to be 2.7 kcal/mol. The transition normal mode (which has an energy corresponding to 72i cm-1) can be viewed from the following four different orientations, and we were again surprised at how dependent the perception of this mode can be on the selected orientation.
Like IF5, the transition state vibrational mode is chimeric with characteristics of the TR, the BPR and lever modes. This again serves to emphasize how a written or even a static diagrammatic description of the mode can fail to reveal the true dynamic character of the vibration. There is one subtle difference between the previous IF5 chimeric pseudorotation and that for IF7; in the former the central iodine atom fully participated in the vibration, with IF7 the participation is much decreased, along with that of one fluorine.
Figure 5. Interactive diagrams illustrating the pseudorotation process for IF7, and generated using the Jmol applet. Click on the thumbnail above to activate the diagram.
We conclude with one final example that illustrates how fluxional processes are relevant to understanding the structure and reactivity of important new classes of molecules. The Sn(amidinate)2 molecule (amidinate= RN=CR'-NR-) we have chosen as our example, serves as a simple analogue of Sn(II) compounds that are being investigated as potential catalysts.26 Calculation of the ground state structure (in agreement with X-ray crystallographic results for similar molecules and with published calculational results)27, shows that the Sn has a coordination geometry of a distorted trigonal-bipyramid in which a lone pair of electrons occupies one equatorial position. The coordination geometry around tin (disphenoidal or "see-saw") is similar to that observed for SF4, although distorted by the geometric constraints imposed by the chelating amidinate ligands. Furthermore, the geometric constraints of the chelating ligands and the coordination geometry about the Sn(II) center result in a chiral molecule of C2 symmetry. The two ground state structures, shown in Figure 6, Structures A and B, are enantiomers. Consistent with published results27c our calculated transition state (Center frame in Figure 6) that links the two ground states is of C2v symmetry. Racemization of the two enantiomers via the mechanism animated in Figure 6 shows the "Berry-like" character of the exchange mechanism. A further examination of the literature revealed Berry pseudorotation as a well established mechanism for the racemization of several P, Sn, Ge and Si compounds.28, 27c
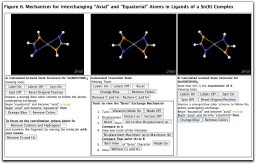
Figure 6. Interactive diagrams illustrating the pseudorotation process for a Sn(amidinate)2 complex and generated using the Jmol applet. Click on the thumbnail above to activate the diagram.
To create the images and animations we built each molecule in CS Chem3D Ultra (Version 7.0)29 and minimized it using the MNDO-d semi-empirical method. We then carried out a Density Functional calculation using Gaussian 03 (typically using the keyword B3LYP/6-31G(3d) or B3LYP/Gen to read in the cc-pVTZ basis set) to optimise the geometry (minimising the energy for the ground states and solving for zero first derivatives of energy for the transition states)12. Vibrational frequencies were calculated for each located transition state, one of which corresponded to the single negative root of the second derivative matrix. The Gaussian output file was read into Jmol Version 9 (which supports normal mode analysis rather better than version 10) and the negative (imaginary) mode was selected.13 This mode was then saved as an xyz file to be visualized using the Jmol 10 applet.13 Equilibrium geometry structures were created by reading the Gaussian output files in Gaussview and re-saving the files in MDL format (mol files).30 To create different views of the equilibrium state structures the mol files were opened in CS Chem3D and rotated to the desired orientation and re-saved.29 All commands to move, manipulate, turn vibrations on and off, label and color the atoms/molecule are scripts supported by the Jmol 10 applet13 with the exception of the process by which we stepped a transition state through one cycle of a vibration from one point of maximum amplitude to the opposite point of maximum amplitude. In this case we simply stepped the molecule though a set of frames within the xyz file with delays between each step. The result appears as a movement in slow-motion through one cycle of the vibration. To enable "web-discovery" of the molecules contained within this article, we have linked each coordinate file within the Web page.
We argue here that an important aspect of teaching about fluxional behavior such as that observed in intramolecular axial/equatorial ligand exchange processes in systems like XY5 and XY7, is for students to be able to view the actual dynamic process, and to be able to move the vibrating molecule into alternative views which corresponds to their own ideal perception of the process. These techniques have led to new insight into how several relatively unstudied molecules undergo such dynamic exchange.
MEC would like to thank Charles "Jim" and Marjorie Kade for their generous support of Carleton College and H. Rzepa and the Department of Chemistry at Imperial College London for sponsoring her while on sabbatical leave.