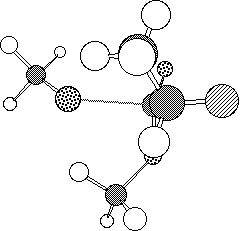
The model reaction between methyl 2-fluoropropionate and methoxide or hydroxide
anion was studied at the PM3 or ab initio 6-31G* SCF-MO levels
respectively, methods which have been successfully applied to stereoelectronic
rationalisation of several other reactions.[8] It can be
envisaged that in the anti transition state (1, Figure 1a) there
is an n-[sigma]* stabilising interaction of the Ahn-Eisenstein type[9], between the active site serine hydroxide nucleophile of
the enzyme and the low energy [sigma]* orbital anti-periplanar to the C-F
bond of the substrate. This interaction is absent in the syn
conformation (2, Figure 1b).

The calculated discrimination in favour of 1 (Figure 1a) is 2.4 or 2.8 kcal mol[-1] at the PM3 or 6-31G* levels respectively (Table). The calculated PM3 entropy difference between 1 and 2 of 0.4 cal K[-1] mol[-1] results in a free energy difference of 2.5 kcal mol[-1 ]at 300K.[ ]Energy differences of this magnitude correspond to a anti/syn ratio of ~100:1. The enthalpy and free energy differences reduce to 1.3 and 0.7 kcal mol[-1] respectively when the PM3-COSMO aqueous solvation model[10 ]is applied, implying a significant reduction in specificity. The origins of these effects are evident in the PM3 energies of the oxy-anion lone pair HOMO orbitals. Those for 1 ~ 0.17 - 0.21 eV more stable than 2 as a result of stabilisation by interaction with the [sigma]* orbital, which also induces a small contraction in the O-C forming bond. The orbital energy differences are reduced to ~ 0.05 eV when the PM3-COSMO model is applied, largely because the oxy-anion orbital is considerably stabilised by the solvation model (Table). This in turn increases the energy difference between this orbital and the unoccupied C-F [sigma]* orbital from ~ 10 eV to ~ 11.5 eV, thus reducing the perturbational stabilisation. It can be expected that a substrate bound to the enzyme will be essentially desolvated at the active site[11], and therefore such stereoelectronic control will be maximised under these conditions.
Models of the common hydrolytic enzymes e.g.(C. cylindracea,[12] pig liver[13] etc.) have been proposed on the basis of substrate/activity profiles which attempt to map the steric constraints of the active sites. In the light of the current study, the efficacy by which individual lipases resolve a-fluorinated esters should afford additional spatial information deduced from the stereoelectronic interactions allowed at that active site.
Theoretical calculations were carried out at the restricted Hartree-Fock level (RHF) PM3 semi-empirical method, as implemented in the MOPAC 93 program,[8 ]using a relative permittivity of 78.4 for water and 60 surface segments per atom for the COSMO model. Ab initio calculations were performed using the Gaussian-92 program. All structures were optimised using the eigenvector following algorithm, followed by a vibrational analysis to characterise the transition state. Use of the COSMO option approximately doubles the computation time compared with a gas phase calculation. Computer readable files for Apple Macintosh and Microsoft Windows systems in Quicktime(TM) video animation format illustrating the three dimensional properties of 1 and 2 are available for general access from the Gopher+ server gopher.ch.ic.ac.uk. These files will reside in the rzepa/Royal_Society_of_Chemistry/Perkin_Trans_2/3_ZZZZZZ directory for a period of at least two years from the publication of this paper. A description of how to visualise such material, together with appropriate programs is available from the same source.
References
1. D. Seebach, Angew. Chem. Int. Ed. Engl., 1990, 29, 1320; J. Mann, Chem. Soc. Rev., 1987, 16, 361; J. T. Welch, Tetrahedron, 1987, 43, 3123.
2. K. Iseki, T. Nagai and Y. Kobayashi, Tetrahedron Letts., 1993, 34, 2169; R. W. Lang, Drug News and Perspectives, 1991, 4, 13; G. L. Hann and P. Sampson, J. Chem. Soc. Chem. Commun., 1989. 1650; E. Differding and R. W. Lang, Tetrahedron Letts., 1988, 29, 6087.
3. D. O'Hagan, N. A. Zaidi and R. B. Lamont, Tetrahedron Asymmetry, 1993, 4, 1703; D. O'Hagan and N. A. Zaidi, J. Chem. Soc. Perkin Trans I, 1992, 947; T. Yamazaki, N. Okamura and T. Kitazume, Tetrahedron Asymmetry, 1990, 1, 521; T. Yamazaki, T. Ohnogi and T. Kitazume, Tetrahedron Asymmetry, 1990, 1, 215; J. T. Lin, T. Yamazaki and T. Kitazume, J. Org. Chem., 1987, 52, 3211; T. Kitazume and J. T. Lin, J. Fluorine Chem., 1987, 34, 461.
4. T. Fujisawa, I. Ichikawa and M. Shimizu, Tetrahedron Asymmetry, 1993, 4, 1237.
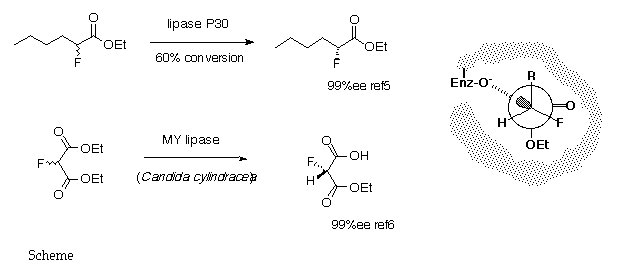
5. P. Kalaritis, R. W. Regenyne, J.J. Partidge and D. L. Coffen, J. Org. Chem., 1990, 55, 812.
6. T. Kitazume, K. Murata and T. Ikeya, J. Fluorine Chem., 1986, 31, 143.
7. L. Dasaradhi and D. O'Hagan, Bio. Med. Chem. Letts., 1993, 3, 1655.
8. O. Casher, D. O'Hagan, C. A. Rosenkranz, H. S. Rzepa and N. A. Zaidi, J. Chem. Soc., Chem. Commun, 1993, 1337; M. S. Baird, J. R. Al Dulayymi, H. S. Rzepa and V. Thoss, J. Chem. Soc., Chem. Commun, 1992, 1323; B. Halton, R. Boese and H. S. Rzepa, J. Chem. Soc., Perkin Transactions 2, 1992, 447
9. S.S. Wong and M. N. Paddon-Row, J. Chem. Soc. Chem. Commun., 1990, 456; N. T. Anh and O. Eisenstein, Nouv. J. Chem, 1977, 1, 61.
10. A. Klamt and G. Shürmann, Perkin Transactions, 1993, 799; H. S. Rzepa, and G. Suñer, J. Chem. Soc., Perkin Trans 2, 1994, 1397; H. S. Rzepa, and G. Suñer, unpublished results
11. M. J. S. Dewar, Enzyme, 1986, 36, 8; W. N. Lipscomb, Acc. Chem. Res., 1982, 15, 232.
12. T. Oberhauser, K. Faber and H. Griengl, Tetrahedron, 1989, 45, 1679; R. J. Kazlauskas, A. N. E. Weissfloch, A. T. Rappaport and L. A. Cuccia, J. Org. Chem., 1991, 56, 2656; K. Hult and T. Norin, Pure & Appl. Chem., 1992, 64, 1129.
13. P. Mohr, N. Waespe-Sarcevic, C. Tamm, K. Gawronska, J. K. Gawronski, Helv. Chim. Acta., 1983, 66, 2501.
Table. Calculated Properties of Transition States 1 and 2.
Figure 1. Calculated PM3 geometry of transition state 1 (a) and
2 (b).