Tri-indenotriphenylene 1 is predicted to be a highly non-planar molecule, with a calculated barrier to inversion of >300 kJ mol[-1] at three different levels of semi-empirical theory. [2] Our own MNDO and PM3 SCF-MO calculations suggest that the origins of this large barrier are largely electronic, since molecular mechanics force fields (e.g. MM3) predict much lower barriers (~ 136 kJ mol-1), arising largely from angle strain. We also note that a barrier of this magnitude appears not to be an artefact of the restricted Hartree-Fock procedure, since in our hands a PM3 spin-unrestricted (UHF) biradical calculation also predicts a significant barrier (383 kJ mol-1). The negative component of the calculated molecular electrostatic potential of 1 is significantly distorted towards the convex face, an effect arising from a decreased p[pi]-p[pi] overlap destabilising the [pi] system on this side, a distorsion which indeed may be a general phenomenon in inducing an electrophilic [pi]-facial preference.
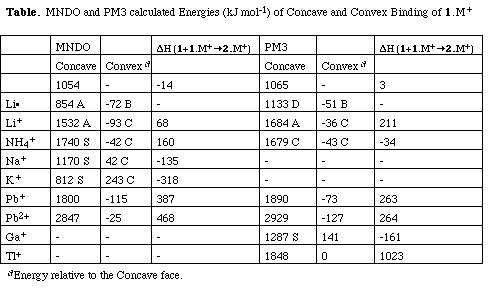
The original reported preference for Li+ binding to the convex face[2] is also reproduced using recently recently published PM3 lithium parameters (Table)[7]. Geometry optimisations starting with Li+ bound to the concave face of any of the four rings A-D result in the ion "creeping" to the outer rim of the system. Calculations on the convex face always gave u[6 ] structures localised to any of rings A-D. The phenomenon did not depend on the oxidation state of the metal, the doublet Li[*]complex showing the same behaviour.[4] The metals Li+,[4] Na+and K+[9] all have a precedent for coordination exclusively by [pi]-carbon ligands and hence the calculated preference of Na+ and K+ for a symmetrical structure with the ion lying in the concave face along the C3 symmetry axis of the molecule did not seem unreasonable, particularly since the MNDO parameters published by Bock[8 ] for Na and K are reported to reproduce molecular geometries well. Only one experimental gas phase benzene binding energy to an alkali metal is available, for Na+ ([Delta]Hexp 117 kJ mol-1)[10 ]. Whilst the predicted MNDO binding energy to benzene for Li+ ([Delta]Hcalc 207 kJ mol-1) appears reasonable in this context, that for Na+ ([Delta]Hcalc 301 kJ mol-1) and K+ ([Delta]Hcalc 362 kJ mol-1) are excessive. This is confirmed by the results at the RHF ab initio level; Li+ 170, Na+ 113 (6-31G* basis) or Na+ 83, K+ 58, Rb+ 49 (ECP-LAN1LDZ basis) and at the MP2/ECP-LAN1LDZ level; Na+ 87, K+ 58, Rb+ 48 kJ mol-1. We note that the LAN1LDZ basis does not include polarisation functions, and hence probably underestimates the binding energies.
We therefore investigated other metals ions likely to bind to the [pi]-face of 1 for which MNDO or PM3 calculations are possible. Several particularly well characterised examples of Ga+ binding are known, including a cyclophane in which tris u6 coordination is the only binding to the metal [11]. Only PM3 parameters are available for this metal, for which a clear concave preference is revealed (Table). As with K+ however, the calculated binding enthalpy of Ga+ to benzene appears excessive (400 kJ mol-1) in comparison to the ab initio values (Ga[+ 97 at RHF/LECP-LAN1LDZ, 124 kJ mol-1 at MP2/ECP-LAN1LDZ, the corresponding values for Tl+ being 80 and 117 kJ mol-1). The magnitude of these values do indicate that Ga+ may bind much more strongly than K+ to a [pi]-face, and hence may be the most likely candidate for encapsulation. Both thallium[12] and ammonium[13] ions are known to exhibit bis u6 coordination to benzene rings, and mono u6 coordination for Pb[2+]is known[14]. For Pb+ there is also an experimental gas phase binding energy to benzene,[10] which is reproduced at the PM3 level ([Delta]Hcalc 100, [Delta]Hexp 109 kJ mol-1). The calculated semi-empirical preference for all these ions is convex binding. The result for thallium reveals the lowest energy isomer to be effectively bound to the rim rather than the edge (Table).
Since 1 can potentially dimerise to C60H24 via a series of six [2+4] Diels Alder cycloadditions, we considered it of interest to calculate the energy of this reaction. In the absence of a metal ion, the dimerisation is approximately thermoneutral (Table). With the exception of Na,+, K+ and Ga,+ the larger metal ions are not predicted at the semi-empirical level to strongly enhance the dimerisation reaction (Table). In particular, Tl+ inhibits the dimerisation, presumably because of its steric bulk. We suggest that Ga+ may be the best candidate for encapsulation, both because of the strength of its [pi]-ligand interactions, and its relatively small size.
Acknowledgements: We thank the European Erasmus scheme for a travel grant (to FS and SS).
MNDO or PM3 calculations were carried out at the restricted Hartree-Fock level (RHF) using the MOPAC 93 program. Parameters for sodium and potassium were those recently reported[8]. Structures were optimized using the eigenvector following method and the XYZ keyword. Ab initio calculations were carried out using the Gaussian-92 program.[15] Searches of the Cambridge structural database for coordinated metal cations were performed using release 5.6 of the Quest software.[16 ] Computer readable files for Apple Macintosh and Microsoft Windows systems in Quicktime(TM) and MPEG video animation format illustrating the three dimensional molecular electrostatic isopotential calculated for 1 are available for general access from the Gopher+ server gopher.ch.ic.ac.uk. These files will reside in the Royal_Society_of_Chemistry/Perkin_Transaction_2/3_07186C directory for a period of at least two years from the publication of this paper. A description of how to visualise such material, together with appropriate programs is available from the same source. An on-line version of this paper is available via world-wide-webb server http://www.ch.ic.ac.uk/RSC/P2/3_07186C.html
Calculated RHF (MP2) energies using the LAN1LDZ/ECP basis set for metal.benzene complex in Hartree; Na -230.6727 (231.1697), K -230.6631 (-231.1588), Rb -230.6594 (-231.1551), Ga -232.4177 (-232.9442), Tl -280.6299 (-281.2270). The size of 1 precludes such calculations.
2. A. J. Edwards, R. Faust, K. P. C. Vollhardt, J. Chem. Soc., Chem. Commun., 1993, 1471.
3. W. N. Setzer and P.von R. Schleyer, Adv. Organomet. Chem., 1985, 24, 353; C. Schade and P. von R. Schleyer, ibid, 1987, 169.
4. D.Bladauski, W.Broser, H.-J.Hecht, D.Rewicki, H.Dietrich, Chem.Ber., 1979, 112, 1380; Hong Chen, R.A.Bartlett, H.V.R.Dias, M.M.Olmstead, P.P.Power, Inorg.Chem., 1991, 30, 2487; D.Bladauski, D.Rewicki, Chem.Ber., 1977, 110, 3920
5.J.L.Seela, J.C.Huffman, G.Christou, J.Chem.Soc.,Chem.Comm., 1987, 1258; R.A.Bartlett, P.P.Power, S.C.Shoner, J.Am.Chem.Soc., 1988, 110, 1966; R.Hunold, J.Allwohn, G.Baum, W.Massa, A.Berndt, Angew.Chem.,Int.Ed.Engl., 1988, 27, 961; H.Hoberg, V.Gotz, R.Goddard, C.Kruger, J.Organomet.Chem., 1980, 190, 315; A. Moezzi, M.M.Olmstead, P.P.Power, J.Am.Chem.Soc., 1992, 114, 2715,; K.M.Waggoner, P.P.Power, Organometallics, 1992, 11, 3209.
6. J.J.Brooks,W.Rhine, G.D.Stucky, J.Am. Chem. Soc., 1972, 94, 7346;.W.E.Rhine, J.Davis, G.Stucky J.Am.Chem.Soc., 1975, 97, 2079. A.Sekiguchi, K.Ebata, C.Kabuto, H.Sakurai J.Am.Chem.Soc., 1991, 113, 1464; T.A. Bazhenova, R.M.Lobkovskaya, R.P.Shibaeva, A.K.Shilova, M.Gruselle, G.Leny, E.Deschamps, J.Organomet.Chem., 1983, 244, 375; A. Sekiguchi, K.Ebata, C.Kabuto, H.Sakurai, J.Am.Chem.Soc., 1991, 113, 1464.
7. E. Anders, R. Koch, P. Freunscht, J. Comp. Chem., 1993, 14, 1301.
8 H.Bock, K.Ruppert, Z.Havlas, D.Fenske, Angew.Chem., Int.Ed.Engl., 1990, 29, 1042; H.Bock, C. Nather and K. Luppet, J. Chem. Soc., Chem. Commun., 1992, 765.
9. K.Hoffmann, E.Weiss, J. Organomet. Chem., 1974, 67, 221; J.L.Atwood, D.C.Hrncir, R.D.Priester, R.D.Rogers, Organometallics, 1983, 2, 985.
10. B. C. Guo, J. W. Purnell, A. W. Castleman, Chem. Phys. Lett., 1990, 168, 1
11. H.Schmidbaur, R.Hager, B.Huber, G.Muller, Angew.Chem., Int.Ed.Engl., 1987, 26, 338,; H.Schmidbaur, W.Bublak, B.Huber, G.Muller, Z.Naturforsch., Teil B, 1987, 42, 142;; H.Schmidbaur, W.Bublak, B.Huber, G.Muller, Organometallics, 1986, 5, 1647.
12. H.Schmidbaur, W.Bublak, J.Riede, G.Muller, Angew.Chem.,Int.Ed.Engl., 1985, 24, 414; S.H.Strauss, M.D.Noirot, O.P.Anderson, Inorg.Chem., 1986, 25, 3850; C.Bianchini, D.Masi, K.Linn, C.Mealli, M.Peruzzini, F.Zanobini, Inorg.Chem., 1992, 31, 4036.
13. W.J.Westerhaus, O.Knop, M.Falk, Can.J.Chem., 1980, 58, 1355.
14. A.G.Gash, P.F.Rodesiler, E.L.Amma, Inorg.Chem., 1974, 13, 2429.
15.Gaussian 92, M. J. Frisch, G. W. Trucks, M. Head-Gordon, P.M.W. Gill, M. W. Wong, J. B. Foresman, B.G. Johnson, H. B. Schlegel, M.A. Robb, E. S. Replogle, G. Gomperts, J. L. Andres, K. Raghavachari, J. S. Binkley, C. Gonzalez, R. L. Martin, D. J. Fox, D. J. Defrees, J. Baker, J. J. P. Stewart, and J. A. Pople, (Gaussian, Inc., Pittsburgh PA, 1992) .
16. F. H. Allen, J. E. Davies, J. J. Galloy, O. Johnson, O. Kennard, C. F. Macrae, E. M. Mitchell, G. F. Mitchell, J. M. Smith and D. G. Watson, J. Chem. Inf. Comp. Sci., 1991, 31, 187.
