Molecular Möbius Strips and Trefoil Knots

With the current interest in so called "nanoscale" devices with dimensions reaching down to molecular sizes, there exists a fascinating boundary between the shapes that materials (i.e. a large collection of molecules) and molecules themselves can adopt. Understanding how molecular building blocks can be used to construct nanoscale devices is the key to understanding nanotechnology. A second boundary exists, between idealised shapes, or topologies, defined by mathematical equations, and the actual shapes adopted by the collections of atoms (nuclei and electrons) we call molecules. The Trefoil Knot and the Möbius Strip are two such topologies which span both boundaries. Here we tell the story from the molecular and electronic perspective. To view the molecular models, you will have to install a program capable of viewing molecule coordinate files.

The Boundary with Mathematics

As a mathematical concept, trefoil knots have many fascinating properties (see the Wolfram MathWorld page from which the adjacent diagrams are taken). The one we concentrate on here is that the trefoil knot also has the property of being a Möbius strip. This topology was first proposed by August Möbius in the 19th Century, and is easily constructed by cutting a closed band into a single strip, giving one of the two ends thus produced a half twist, and then re-attaching the two ends. The mathematical properties of Möbius strips are both fascinating and complex, but of equal interest (to a chemist!) is whether a molecule or a nanoscale material can be induced to adopt such a shape, and if so, what its properties might be.

As it happens, two somewhat different kinds of molecular Möbius strip can be envisaged; those where the nuclear framework itself is twisted into a Möbius strip and those where only the electronic component of the molecule, described by a wavefunction, has this property.

Molecules with Nuclear Möbius strips

Trefoil knot The first step to constructing a Möbius strip using molecules is to create the molecular equivalent of a strip of paper. This is done by starting with benzene, and extending it by adding a series of benzo groups to turn it into napthalene, anthracene and so on, forming what is called a poly-acene. The two ends of this strip are then twisted and joined to form what is called a Möbius cyclacene. Models for such systems containing one, two or three twists can be constructed.¹ Although these molecules contain far too much strain induced by the twisting to be likely to be actually made, their properties can be modelled using quantum mechanics. Unlike a true Möbius strip, where the "twist" is evenly distributed along the entire length of the ring (see the Mathworld models) these molecular strips appear to "localise" the twist to a relatively small region of the molecule. The implications of this unexpected property are still being investigated.

Molecules with Electronic Möbius strips

To twist just the electrons in a molecule into a Möbius strip requires some way of persuading them that it is in their (energetic) interest to do so. The story of how this can be done dates back to another August, this time August Kekulé. In middle of the 19th century he suggested that the then recently discovered (and unexpectedly stable) benzene molecule had a structure consisting of a cyclic arrangement of the atoms. Following suggestions by the discoverer of the electron J. J. Thompson (Phil. Mag, 1921, 41, 510) and E. C. Crocker (J. Am. Chem. Soc.,, 1922, 44, 1618) and --> Armit and Robinson (J. Chem. Soc., 1925, 1604) of the special significance of an "aromatic sextet", Erich Hückel developed theories of molecular quantum mechanics which were eventually used to show that such cyclic molecules, known as aromatics, were particularly stable when 2,6,10,14,18 etc (generally 4n+2, where n is zero or a positive integer) electrons occupied a cyclic and parallel overlapping arrangement of atomic p-orbitals (the "Hamburger" model. The two buns can be thought of as representing the electrons in the molecule and the meat patty the nuclei). The resulting electronic stability imparts to such molecules a property known as aromaticity, of which benzene remains the best known example. In 1964 Edgar Heilbronner² worked out that cyclic molecules with 4,8,16,20 etc (generally 4n) electrons could be equally aromatic, but only if a twist was given to the otherwise parallel overlap of the p-orbitals, a twist which corresponds exactly to the Möbius twist! Amazingly, it has taken some 40 years for chemists to actually propose candidates for such molecules. Some of the newly discovered (or invented) Möbius electronic systems include: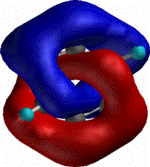

a ring of 16 CH units known as [16]-annulene³ (benzene for example has 6 such units and could be called [6]-annulene)
a ring containing four selenium atoms⁴
an allotrope of nitrogen with 12 atoms⁴, which if it were ever to be made, would no doubt be highly explosive!
and systems consisting of three Möbius rings sharing a single central atom (phosphorus).⁵

These molecules all exhibit (see right) a cyclic Möbius-like twisting of the electrons (or more accurately, of the electronic wavefunction).
Knotted protein

The last example above, in which three twisted rings were joined at a single atom, brings us to the mathematical shape known as the Trefoil Knot. By imagining a molecular chain of 36 carbon atoms, but this time not joining it at a central atom, a molecular Trefoil knot can be constructed. Such an isomer of carbon, were it possible to make, would join the list of known carbon allotropes such as graphite, diamond and buckyballs. A more realistic chemical model can be made by attaching benzo groups to the outside to make a hydrocarbon (benzo groups are derived from the molecule that started this story, benzene). This "invented" molecular trefoil knot has both the characteristics of a nuclear and an electronic Möbius strip.

Nature is, unsurprisingly, ahead of us in invention. Although they are only nuclear and not nuclear-electronic Möbius strips, some molecules have indeed been persuaded to wind themselves into a trefoil knot!⁶ Nature is also capable of knotting proteins (large molecules or biopolymers, made of long chains of connected amino acids). The active site of one such protein (shown on the left) is constructed right on a trefoil knot!⁷

The Boundary with Nanoscale materials

To complete the scaling up of this concept, some Japanese workers have recently reported⁸ that the inorganic conductor NbSe₃ can grow tiny crystals which take the form of Möbius strips. The authors write at the end of their article that "Our crystal forms offer a new route to exploring topological effects in quantum mechanics as well as to the construction of new devices", which could probably be said for several of the other usual Möbius systems described here. Thus an area of chemistry 180 years old, started with Faraday's discovery of benzene in 1825, continues into the 21st century!

Molecular Möbius Strips and Trefoil Knots

The Boundary with Mathematics

Molecules with Nuclear Möbius strips

Molecules with Electronic Möbius strips

The Boundary with Nanoscale materials

Further Reading