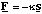3.1 Simple Harmonic Motion

We will now go on to examine how the conservation of energy can be used to solve the equations of motion for an oscillating diatomic molecule.

Imagine a molecule made of two atoms of mass m1 and m2, held together by a bond of equilibrium length r0 and bond stiffness κ. The force which will be exerted if we stretch or compress the bond will act in such a way as to return the molecule to its equilibrium bond length. If the extension s is relatively small the force will obey Hooke's Law

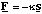(3.1.1)

where the negative sign ensures the force always acts in the opposite direction from the extension, figure 3.1.1.

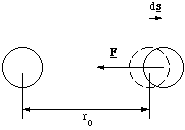
Figure 3.1.1. The restoring force.

Then the potential energy for extension or compression of the bond is given by the negative of the integral of the force with respect to extension

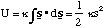(3.1.2)

(U = 0 at s = 0). The total energy of the system is composed of the potential and kinetic energies, so we will now determine the kinetic energy. Since we are looking at an internal motion of a system of particles, the total kinetic energy of the molecule is given by

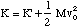(3.1.3)

where K' is the kinetic energy of the oscillating molecule and the second term is the translational kinetic energy of the molecule, total mass M = m1 + m2, and centre of mass velocity v0. At present we will assume v0 = 0. K' is given by the sum of the kinetic energies of each atom.

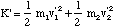(3.1.4).

We will now go on to find a more convenient way of expressing K', which you will find used in spectroscopy. We begin by writing down the relative velocity, vr, between the atoms

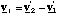(3.1.5).

Now since no external forces, Fext, are acting on our two atoms, but only the internal spring like force, we can invoke the laws of conservation of momentum

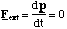(3.1.6)

and hence

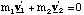(3.1.7).

We can find the velocities v1' and v2' in terms of vr.

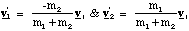(3.1.8).

Substitution of these velocities into our equation for K' gives us

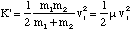(3.1.9)

where μ is called the reduced mass of the diatomic molecule.

On the assumption that no external forces are acting on the diatomic molecule the First Law of motion tells us that even if v0 is non zero, it will be constant. We already know that changes in the potential energy due to bond extension will be accompanied by compensating changes in kinetic energy. These can only therefore occur due to variations in K' . In this way the energetics of the translational motion of the molecule are de coupled from the internal energy.

In this centre of mass frame the conservation of energy becomes

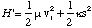(3.1.10),

where H' is the total energy. The relative velocity in this frame is simply ds/dt, and hence we have

(3.1.11)

which is a first order differential equation. We could stop at this point and ask Mathematica to solve this, but the equation is sufficiently simple that we can solve it without. To do this we re-express (3.1.11) as

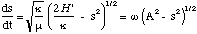(3.1.12)

with ω = [[radical]](κ/μ) and A = [[radical]](2H'/κ). Equation (3.1.12) can then be re-arranged to give us the following integral to solve

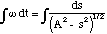(3.1.13)

The solution to which is

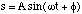(3.1.14)

where ω is called the circular frequency and φ is the initial phase, i.e. the displacement of the atoms at t = 0, figure 3.1.2. The period, T, of the oscillations (the time it takes for the system to return to its initial position) is given by T = 2π/ω. It is important to note that the period of the oscillations is entirely independent of the amplitude of the oscillations A.

From the graphs it can be seen that increasing the bond stiffness increases the oscillatory frequency and decreases the amplitude. From the definitions of ω and A it is clear that an increase in κ by a factor of four doubles the frequency and halves the amplitude. Increasing the reduced mass decreases the frequency, but leaves the amplitude unchanged. A quadrupling of the reduced mass will halve the frequency. As expected, changing the internal energy only changes the amplitude, but not the frequency of the oscillating molecule.

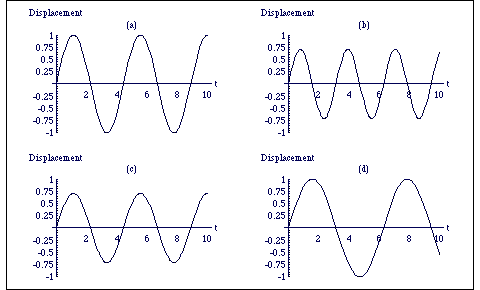
Figure 3.1.2. Plots of the diatomic separation as a function of time; all scales are arbitrary and the phase is always zero. In (a) H' = 1, κ = 2, m = 1, in (b) H' = 1, κ = 4, m = 1, in (c) H' = 0.5, κ = 2, m = 1 and in (d) H' = 1, κ = 2 and m = 2. (For code see "Physical Chemistry:Molecular Interactions: SHM").

3.1.1 Conditions for Simple Harmonic Motion

A sensible question to ask is why SHM explains the oscillatory motion of so many different chemical systems? We begin by imagining a potential energy curve, which will have a minimum at the position r0, i.e. one in which a chemical bond exists. Now we may not now the mathematical form of our potential energy curve, but we do know that some polynomial expansion about r0 will fit the potential energy curve over some range of displacements, figure 3.1.3.

This expansion will have the general form

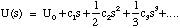(3.1.15).

The force is found by differentiating U(s) with respect to s

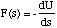(3.1.16),

which gives

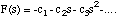(3.1.17).

Since F(0) = 0 we have that c1 = 0 and so

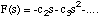(3.1.18),

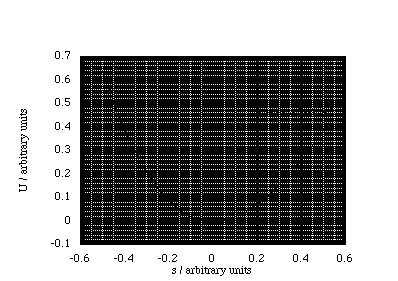
Figure 3.1.3. A polynomial expansion can always be created to accurately model the potential energy as a function of displacement. Note the steeper repulsive slope at negative displacements (bond compression).

so in some suitable range of s the s² term will always be insignificant with respect to the linear term and the force will follow Hooke's Law. This will generally be when the displacements are small. Here

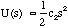(3.1.19).

If s gets large, you can see that higher order terms will become important. Furthermore the coefficient c2 is the bond stiffness κ which is therefore given by

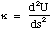(3.2.20).

3.1.2 Stable and Unstable Equilibrium

It is evident from the shape of the potential energy curve of the harmonic oscillator that any perturbation of the system, i.e. displacement of the atoms, will lead to the system wishing to return to the equilibrium position, because this is the point of minimum potential energy, figure 3.1.3.

Another way of putting this is to say that the gradient of the potential energy is zero and hence so is the force. However, this does not establish the crucial point, that any small perturbation away from equilibrium gives rise to a negative, restoring force. In other words it does not establish the fact that this position is one of stable equilibrium. For this to be true k must be positive and hence we can say,

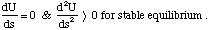
In cases where the second derivative of U with respect to displacement is less than zero the potential energy surface slopes downhill as we move away from equilibrium. In other words this is a state of unstable equilibrium, any small perturbation from equilibrium leads to a decrease in potential energy. This sort of situation frequently characterises the energetic barriers which need to be overcome for a reaction to occur, whereas the situation of stable equilibrium characterises the bonded state.