2 Particle Dynamics
Molecular dynamics is the study of how and why molecules move in the way that they do. Before Newton, Aristotle said that bodies move only because other bodies cause them to do so. This perfectly reasonable suggestion was turned on its head by Newton who said that bodies would continue to move at a uniform velocity unless acted upon by a force which produces an acceleration on the body.
2.1 Measuring Motion - Kinematics
Before we can grapple with Newton's ideas and apply them to the motions of things like atoms, ions and molecules we will need to learn how we can measure their motion.
2.1.1 The Centre of Mass
All atoms and ions consist of a nuclear core made of protons and neutrons, surrounded by a number of electrons. Although it is rather difficult to say what the exact size of very small objects is, we do know that the nucleus is about 10-15 m in diameter, and the atom is of the order of 10-10 m across. Estimating the electron's size is rather difficult, and rather dubious, nevertheless it's diameter is roughly the same as the nucleus'. This makes it rather obvious that atoms are not mathematical points of mass, they are extended objects. Indeed on their own scale they are extremely spread out over space. If this is so for atoms it is clearly even truer for molecules.
It might therefore seem that in order to describe the motion, or kinematics, of atoms and molecules we will be forced into the complex task of specifying the position of every component as it speeds through space. In fact later on in this course we will prove that there is a single, special point within the molecule whose motion is very easy to describe. This point is called the centre of mass, and it is the point where all the mass of the atom or molecule might be considered to reside.
For example the position of the centre of mass, X, of the diatomic molecule shown in figure 2.1.1 is given by
(2.1.1).
By using the centre of mass to describe the motion of a molecule we have lost the ability to describe the rotational and vibrational movements, we are only able to describe the motion of the entire molecule as if it were a point particle. This means that we can only explain molecular movement caused by forces external to the molecule using this particulate picture. The vibrational and rotational motions, which are internal to the molecule, have no effect on the overall trajectory of the molecule through space. In the language of physics the internal motions are said to be de coupled from the external ones. This will turn out to be a very powerful idea which we will use repeatedly.
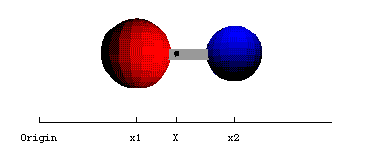Figure 2.1.1. The
centre of mass of a diatomic molecule (for code see "Physical
Chemistry:Molecular Interactions: Diatomic Centre of Mass").
2.1.2 Defining Position, Velocity and Acceleration - in One Dimension
To study the motion of a particle we must be able to track its position with respect to time. We will do this by setting up a measuring line parallel to the particle's trajectory, let this be the x axis, and start a clock running to record the time t. The origin of the x axis and the zero point for our timing are entirely arbitrary.
We can now create a graph of position along the x axis as a function of time, figure 2.1.2.
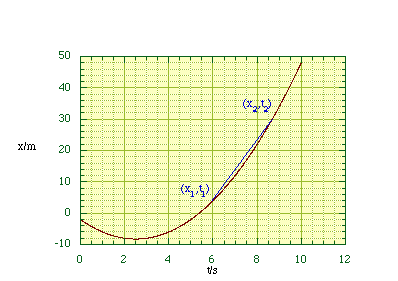Figure
2.1.2. A graph of particle position as a function of time.
The average velocity in moving from position x1 to position x2 in the elapsed time t2 - t1 is given by
(2.1.2)
The velocity has both magnitude and direction, e.g. in figure 2.1.2 the particle is moving in the negative x direction for the first 2.5 s before subsequently moving in the positive x direction. In the language of mathematics this means that the velocity is a vector quantity, it has both magnitude and direction. The speed, which is only the magnitude of the velocity, is called a scalar quantity.
In general plotting x as a function of time does not result in a straight line, i.e. uniform velocity. In these more general cases we define the instantaneous velocity at some specified position to be given by reducing the interval Δt to an infinitely small value, dt.
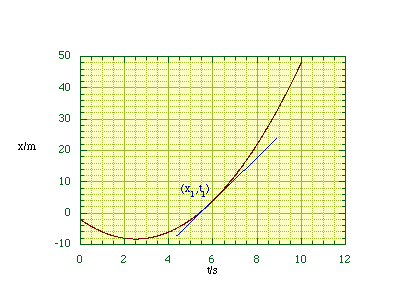Figure 2.1.3.
Determining the instantaneous velocity.
We are therefore measuring the slope or tangent at (x1, t1), figure 2.1.3. In mathematical terms this is symbolised
(SI units ms-1)
(2.1.3)
where dx/dt is the instantaneous rate of change of distance with respect to time. By measuring the slope of our graph at all x as a function of t we can construct a graph of v against t, figure 2.1.4. In many cases there may be a mathematical relationship between x and t , symbolised x = x(t), and we can then find an expression for the velocity by differentiation of x with respect to t.
If the velocity has been varying with time, as it does in our example, then we can also measure the instantaneous rate of change of velocity, or acceleration, a
(SI units ms-2)
(2.1.4).
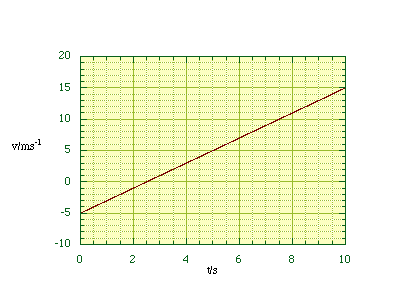Figure 2.1.4. The
velocity - time graph.
Again this is a vector quantity, and as we will see it plays the primary kinematic role in Newton's description of particle dynamics. If, as is the case in our example, the velocity is linearly proportional to the time then the acceleration is constant, figure 2.1.5.
Figure 2.1.5. The
graph of acceleration against time. Acceleration is constant at 2 ms-2
in this example.
2.1.3 Linear Motion under Constant Acceleration
The particle under constant acceleration, shown above, is a simple, but useful case, of particle kinematics with an analytic expression.
If a is constant then by definition so is dv/dt and v = v(t) will be a straight line. A generic straight line graph has the simple form y = mx + c. In this case y is the velocity and x is the time, and the gradient m is a, whilst the constant c is v0, the velocity at t = 0. Hence
(2.1.5).
We can derive this more formally by integration. By definition, after a small interval of time dt the accompanying change in velocity dv will be given by dv = a dt. If we want to know the total change in velocity from t = 0 to t = t, we must add up each little change in velocity between 0 and t (and hence between v = v0 and v = v). This is formally expressed as follows
(2.1.6)
and for constant acceleration the result of this simple integral is given
by
(2.1.7)
which is identical to (2.1.5). However, you should note that the integral expression is extremely powerful since it can solve our equation of motion even when a is not constant. This situation is the general rule in atomic and molecular interactions.
We now re-write the expression for the velocity replacing v by dx/dt
(2.1.8).
We can find x as a function of time by solving the integral
(2.1.9)
where x = x0 at t = 0. Solving the integral gives us
(2.1.10).
Equations (2.1.7) and (2.1.10) express the time dependence of the velocity and position. The dependence of the velocity on position may also be found by substituting for t in equation (2.1.10) using (2.1.7). This gives
(2.1.11).
2.1.4 Motion in Three Dimensions
So far we have confined ourselves to motion in one dimension. We will now extend our description to the three dimensions of space. In doing this you should appreciate that everything we have so far done has in fact been expressed in such a way that its use in three dimensions will require no change to the form of the fundamental equations, we simply need to know how to express position, velocity and acceleration as three dimensional vectors.
The position vector r, defining the position of a particle can be thought of as an arrow pointing from the origin to the particle
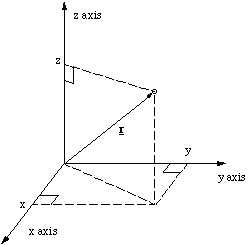
Figure 2.1.6. The position vector.
To get from the origin to the particle we have to walk x steps along the x axis, y steps in the y direction and z in the z direction. We can express this in a compact form as
(2.1.12)
where 
are vectors of
length 1, called unit vectors, directed along the x, y and z axes respectively
and x, y and z are simply the multipliers which tell us how far to move along
each axis (the magnitude) and in which direction (the sign). In the one
dimensional case described in [[section]]2.1.2 and 2.1.3 we effectively set y =
z = 0.
If we now wish to determine the velocity of the particle we must measure the position of the particle at time t, r(t), and a small time Δt later, r(t+Δt). The vector Δr = r(t+Δt) - r(t) is therefore the movement made by the particle in Δt.
In the limit that Δt becomes infinitely small we can determine the instantaneous velocity v = dr/dt
(2.1.13).
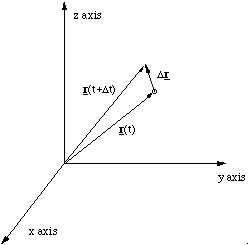
Figure 2.1.7. The displacement vector.
Expanding the vector out into components we get
(2.1.14)
which results in the simple expression
(2.1.15).
Without going into the details, it is clear that we will get exactly the same sort of expression for the acceleration.
(2.1.16)
The most important aspect of these expressions for velocity and acceleration is that the vector is composed of three mutually independent components. This means that if a force is applied to an atom or molecule along the z axis, only the velocity in this direction will be changed. Since no force acts along the other directions Newton's laws of motion tell us that these components of the velocity will remain unchanged.
This makes it clear that choosing the orientation of ones co-ordinate system for a given problem can make its solution far easier than it might otherwise be. In many atomic and molecular systems the natural co-ordinate system is not Cartesian as here, but spherical or cylindrical. Nevertheless such a co-ordinate system and its associated vectorial description will always consist of three mutually independent component (a radial distance and two angles for spherical co-ordinates).
2.2 Force and Momentum
2.2.1 Newton's Laws
Newton hypothesised that there were three fundamental laws of motion.
Law 1
"A particle not acted upon by other bodies moves with uniform velocity."
This statement is extremely counter-intuitive. Our general experience is that we must push or pull things to make them move, but when we discontinue exerting such forces it stops moving. Newton hypothesised that this everyday experience demonstrated that additional forces were acting on the particle to slow it down. These are of course the frictional forces!
Law 2
"The application of a force to a body gives rise to an acceleration in inverse proportion to its mass."
This means that if we apply a force to an object we will cause its velocity to change. According to the first law we can only cause the velocity to change while applying the force. Once we stop applying the force the object carries on its way at constant velocity. The second law further states that if we apply a given force to an object we will cause it to accelerate less the greater its mass. In other words the more massive an object the harder it is to get it to change velocity. With this picture in mind the mass is often called the inertial mass. This also underlines the difference between the mass of an object, which relates to the amount of matter it is composed of, and its weight, which relates to the gravitational force exerted on the object. In chemistry, the gravitational force plays no significant role in molecular and atomic behaviour, so we will always be interested in inertial mass, not weight.
Clearly the force is a vectorial quantity. Pushing an object in the positive x direction has a different kinematic result from pushing it in the negative z direction. This leads us to the following compact mathematical form
F = ma (SI units Newton (N) = kgms-2) (2.2.1)
The second law is seemingly very simple, indeed it is this very simplicity that gives it its universal applicability. This of course means that it is in fact an extremely profound expression!
Law 3
"For every action there is an equal and opposite reaction."
This rather obscure statement means that if a body A acts on body B with force FAB then B acts on A with a force FBA = - FAB. Again this is very counter-intuitive. We are used to pushing something and watching it move away from us, whereas in fact both objects are pushing against each other and hence moving apart. We remain fixed with respect to the ground as we push a chair, only because of the friction between us and the floor.
2.2.2 Electrostatic Force
The use of forces is an everyday experience which we rarely think of. We push or pull an object and we can make it accelerate, as Newton's second Law predicts. We feel direct contact between us and the object being accelerated, but is this picture helpful on the molecular scale? The answer is, strictly speaking, no.
As we have already seen atoms and their kin are for the most part empty space. Forces on this scale act not by direct contact, but through some rather mysterious action at a distance. In fact when you push an object the contact you feel is these forces acting across the regions of empty space between the molecules on the surface of your hand and the molecules on the surface of the object.
The predominant source of the forces acting between atoms and molecules are electrostatic. In 1785 Charles Augustin de Coulomb made an experimental determination of the force between two charged particles. He found that the force was proportional to the product of the charge, being attractive if the particles had opposite sign and repulsive if they had the same sign, and that the force decayed in magnitude in proportion to the inverse square of their separation. Furthermore, the force experienced between the charged particles was always directed along the straight line connecting the two particles.
The electrostatic force between two ions is therefore
(2.2.2)
where F12 is the force exerted by particle 1 on particle 2, q1 is the charge on particle 1 and q2 that on particle 2, r is the distance separating the particles and ê12 is a radial unit vector pointing from 1 to 2. The constant of proportionality is also a universal constant, ε0, the permittivity of the vacuum. The factor 1/4πε0 is equal to 8.99x109 Nm2C-2. The Coulomb (C) is the SI unit of charge and the electron has a charge of -1.6x10-19 C. The charge on the proton, the charged component of the nucleus, has the same magnitude, but is positive.
If q1 and q2 have the same sign their product will always be positive. Since ê12 points from 1 to 2 the force is both repulsive and acting along the line joining the ions, as required by Coulomb's observations, figure 2.2.1.
We have expressed Coulomb's law using a spherical co-ordinate system and hence a radial unit vector, because this is the most compact form we can write. It is however possible to write Coulomb's law using the Cartesian co-ordinate system. If particle 1 is at position r1 and particle 2 is at position r2, the vector pointing from 1 to 2 is then r12 = r2 - r1. The square of the ionic separation is then r12.r12 (the vector dot product) and the unit vector pointing from 1 to 2 is r12/[[radical]](r12.r12). Hence
(2.2.3).
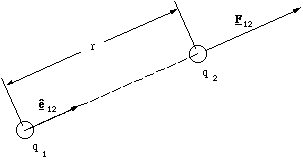
Figure 2.2.1. The Coulomb interaction.
2.2.3 A Collision Between Two Ions
We are now apparently in a position to predict the dynamical behaviour between interacting charged particles. As an example of what we can do, let's look at what would happen in a very simple collision between two ions. The collision we will look at is one in which two ionised hydrogen atoms are approaching each other head on. We set up our x axis to lie in the same direction as the flight path of the protons.
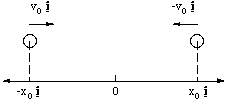
Figure 2.2.2. The colliding protons.
The protons have the same speed v0 at t = 0, but in opposite directions , and are separated by a distance 2x0 at this time. Since both particles have the same mass, m, and charge e it is clear that they will behave as mirror images of each other, so we will simply investigate the dynamics of the proton on the right hand side.
What we will determine is the behaviour of x(t) and v(t). To do this we will have to solve Newton's law for this system. In this case setting up the initial equation is rather trivial, the force, given by Coulomb's Law is equal to the proton's mass times the acceleration on the proton and is in the positive x direction.
(2.2.4)
At this point we are stuck! This is a second order differential equation which has no analytical solution. However, we can solve the equation using numerical method and the results are shown below .
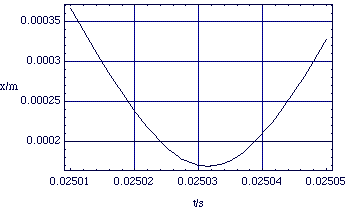
Figure 2.2.3. x(t) for the colliding proton, using m = 1.7 x 10-27 kg, x0 = 0.5 m and v0 = -20 î ms-1 (for code see "Physical Chemistry:Molecular Interactions: Colliding Ions").
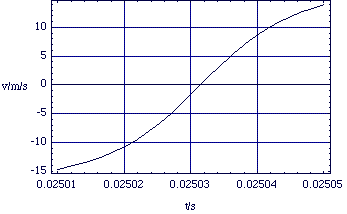
Figure 2.2.4. v(t) for the colliding proton using the same values as above.
The first thing to notice is that the simple dynamical equation (2.2.4) gives rise to quite complex kinematics; this is not a case of constant acceleration. Nor indeed do the ions ever come into contact; the Coulomb repulsion is extremely strong.
This is all fine and well, but must we always do these complex calculations if we want to examine the effects of molecular collisions? Fortunately, the answer is no, as long as we are not too concerned with the details of what goes on when the molecules are close together and interacting strongly. We can see this if we look at the previous collision experiment, but over longer time scales.
At these scales we can see some simple behaviour. The magnitude of the velocity (20 ms-1) before and after the collision is the same and the position as a function of time is a straight line function either side of the collision. We now go on to see how we can formalise these experimental observations.
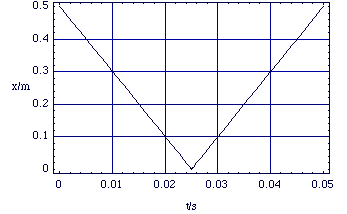
Figure 2.2.5. x(t) over longer time scales.
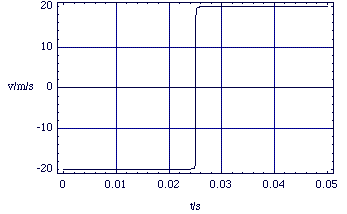
Figure 2.2.6. v(t) over longer time scales.
2.2.4 The Conservation of Linear Momentum in Collisions
During a collision a force due to particle 1 acts on particle 2. This force must vary with time, so we will call it F12(t) (you may be able to determine what the form of this is in the ion collision in [[section]]2.2.3). According to the second law of motion this force will cause an acceleration in proportion to the mass m1
(2.2.5).
If we integrate this force over the duration time for the interaction, t, we get
(2.2.6)
where u1 is the first particle's velocity at t = 0 and v1 is its velocity at t = t. Of course particle 2 exerts an equal and opposite force on particle 1 giving us a second relation
(2.2.7)
but since F12 = -F21 we get
(2.2.8)
and hence
(2.2.9)
which is re-arranged to give us
(2.2.10).
The product of a particle's mass and velocity is called the linear momentum, and it is the total momentum of the system of particles which is conserved before and after a collision. Returning to our ionic collision the fact that the initial and final velocity were equal and opposite is predicted correctly. It was able to make this prediction without needing to know anything at all about the interaction between the ions. It is interesting and important to note that the conservation of linear momentum holds even when the interactions are quantum mechanical. Indeed the law has never been found to be contradicted in any experiment.
We can generalise the law of conservation of momentum by noting that mass may be exchanged during collisions, i.e. a chemical reaction. We therefore give the momentum the symbol p and take this to mean that both mass and velocity may have been altered during the collision. Equation (2.2.10) then becomes
(2.2.11)
where superscript i means initial state and f means final state.
We can extend the conservation law further to include more than two bodies in a rather straightforward manner
(2.2.12).
Notice that the summations on either side of the equality do not necessarily extend over the same number of particles. This takes into account the possibility that new species have been destroyed or created during the collision. Furthermore you will find that in the quantum mechanical world even massless particles like the photon (a corpuscle of light) has momentum and this must be included in order for the equality to hold.
We can re-express this in words.
"The total momentum of a system of colliding particles remains unchanged by the collision. The total linear momentum is conserved."
Surprisingly Newton did not discuss the concept of momentum in Principia. Momentum and its use in understanding collisions was the result of a meeting held in 1668 (the year after Principia was published) at the Royal Society, in which John Wallis (a mathematician), Christopher Wren and Christian Huygens presented papers on collision phenomena. This work led to a reformulation of Newton's Second Law in a more general form
(2.2.13).
2.3 Electrostatics
We have already looked at the force between two point charges in our discussion on collision theory. We now turn to a more general discussion of electrostatics theory.
2.3.1 The Superposition Principle and the Electrostatic Dipole
If we wish to determine the net force exerted by a collection of charged particles on one other, which we will call the test particle, we do this simply by determining the vector sum of electrostatic forces. An important example of this idea in Chemistry is the force exerted by an electrostatic dipole on a charged particle. (Dipolar molecules abound in Chemistry, e.g. HCl or NaCl in the gas phase.)
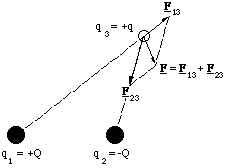
Figure 2.3.1. The principle of superposition using the dipole as an example. The dipole, is made of the charges +Q and -Q.
Figure 2.3.1 illustrates the principle of superposition pictorially. A rather simple example of how the net force is actually calculated is to determine the force on a positive charge placed along the axis of the dipole as shown below.
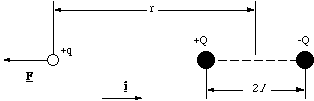
Figure 2.3.2. The dipolar force acting along the molecular axis.
We will set the origin for the x axis at the middle of the dipole. The test charge +q is therefore at the position -rî. Measuring the other distances similarly, the net force on the charge +q is given by
(2.3.1).
Using 2l = 1.5 Å and q = Q = 1.6 x 10-19 C we can plot the force exerted by the dipole on +q along the dipole axis, figure 2.3.3. In most physical situations r is much larger than l and then one can simplify (2.3.1) by using the binomial theorem to expand the denominators and then discarding all terms greater than first order in l/r.
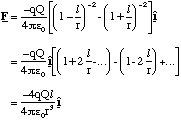(2.3.2)
Data points calculated using (2.3.2) have been plotted as circles on top of the force calculated from (2.3.1), plotted as a solid line. The vertical lines around r = 0 Å are due to problems in calculating the force close to the dipole charges.
Conventionally we define the dipole moment vector 
.The vector points from the negative to the
positive charge and has a magnitude given by the product of the dipole charge
and distance between the charges. Hence the axial force at large distances from
the dipole is given by
(2.3.3).
So here we have an intermolecular interaction which, at least along the molecular axis and at long distances, has a 1/r3 dependence rather than 1/r2. This makes the forces exerted by dipoles shorter range and in general weaker than those due to single ions.
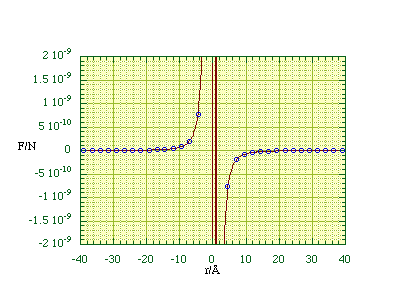Figure 2.3.3.
The axial force due to an electrostatic dipole.
2.3.2 The Electrostatic Field
You may have noticed that the charge +q of our "test" particle factored out of the determination of the force on it. This is a general phenomena when making calculations using superposition and suggests that one can define a new vector quantity, the electrostatic field E, defined by
(SI units of NC-1)
(2.3.4)
In other words the electric field at a position r represents the force that a unit positive charge would experience at that position. This is of course extremely convenient since we can, in principle, determine the field due to any collection of charged particles, which will subsequently allow us to determine the forces which would be experienced by a particle moving in this field. It should however be realised that this assumes that the particle moving in the field has little or no effect on the positions of the charges creating the field. In some situations this is a fair approximation to the truth, for example the conduction electrons in a solid do not disturb the lattice greatly, in other cases it is a severe distortion, for example in the solvation of ions.
For the example of a dipole and the force it exerts at relatively large distances along the molecular axis, we can sensibly calculate the field
(2.3.5)
2.3.3 Representing the Field - Field Lines
It is very informative to make visual representations of fields. They allow one to build up a qualitative picture of both the magnitude and the direction of the force another charged particle might experience in the presence of the field. We look at the field from a positive point charge first. The electrostatic field vectors must all be pointing away from the positive charge, since the field is defined for a positive test charge. If we draw the field vectors tail to head originating from the point charge we also know that they follow a straight line and decrease in magnitude in inverse proportion to the square of the distance. If we look at such a field representation in a plane that bisects the positive charge it should look something like, figure 2.3.4.
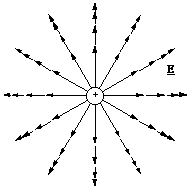
Figure 2.3.4. Field lines around a positive point charge. First style.
This suggests the simpler and more standard representation, where the end to end field vectors are drawn as continuous field lines. The density of the field lines then represents the magnitude of the field.
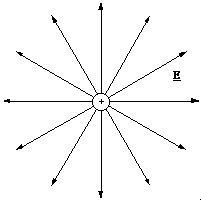
Figure 2.3.5. Field lines around a positive point charge. Second style.
The rules for drawing field lines for an arbitrary collection of charged partices can be summarised as follows.
* Lines start at a positive charge and finish at a negative charge and
must be continuous and smooth.
* Lines do not cross. The field is single valued at all points in space.
* The line density is proportional to field strength.
* Close to any point charge the field is always radial.
We can therefore sketch the appearance of the field around a dipole in the plane running through each charge, by using these rules.
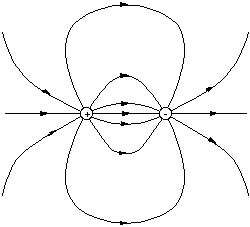
Figure 2.3.6. Sketch of the dipole field.
Three dimensional vector field representations can be generated on Mathematica (for code see "Physical Chemistry:Molecular Interactions: E Fields").
2.3.4 Van der Waals Forces
Van der Waals forces are even weaker than the forces exerted by dipoles on ions. They are present in all atomic and molecular interactions, but because they are weak they are often masked by other forces which are also at play. However, they play important roles in many chemically interesting systems, for example in the stabilisation of bilayer membrane stacks and the binding of anaesthetics. Van der Waals forces actually cover three different types of inter atomic and intermolecular interactions: dispersion forces, dipole-dipole forces and dipole-induced dipole forces. We will deal with the first of these, leaving you to read about the others.
If we consider an electrically neutral and chemically inert atom, such as Xenon, we would imagine that the electron cloud would be disposed entirely symmetrically around the positively charged nucleus, and therefore there would be no net field from such an atom. This however is not the case. The distribution of electrons fluctuates over time, because of quantum mechanical effects. In other words, although the electron distribution is on average spherically symmetrical, much of the time the distribution will be asymmetrical or dipolar and will produce an associated dipolar field.
(2.3.6).
Let us now consider a second Xenon atom at a distance r away from our instantaneous dipole. The effect of the field due to the fluctuational dipole will be to pull the negatively charged electron cloud towards it and repel the positively charged nucleus away. For obvious reason this second dipole is called an induced dipole and it has a dipole moment, P, which need not necessarily be the same as that of the fluctuational dipole.
Figure 2.3.7. The fluctuational dipole on the left hand side of the picture induces a dipole momentr in the molecule to the right.
The field acting on -q' is E(r - l'), meaning E at a distance r - l', similarly the field acting on +q' is E(r + l'). The net force on the induced dipole is therefore
(2.3.7)
where the origin of the term ΔE/Δr is shown in figure 2.3.8 and for r >> l', ΔE/Δr becomes dE/dr.
Remembering that the induced dipole, P', points in the opposite direction to the field from the fluctuational dipole we get
(2.3.8)
where I have removed the vector notation to simplify the problem. Doing the differentiation we get
(2.3.9.
The negative sign means the force is in the opposite direction to the field, i.e. towards the fluctuational dipole.
Figure 2.3.8.
The slope approximation.
The final step in deriving the van der Waals dispersion force is to say that in trying to pull the electrons and protons of an atom apart it behaves like a spring. This means that the extension l' and hence P' would be proportional to the applied force, i.e. proportional to 1/r3. Substituting this dependence for P' we find
(2.3.10).
The same dependence on distance is found for dipole - dipole interactions and for dipole - induced dipole interactions.
2.3.5 Other Inter-Atomic and Inter-Molecular Forces
So far we have been able to use classical electrostatics and the theory of superposition to explain ion - ion, dipole - ion, dipole - dipole, dipole - induced dipole and dispersion interactions. A number of important, ubiquitous interactions remain, which are not explicable in terms of classical Physics.
The first, best known and most common of these is the covalent bond. This is intermediate between ionic bonding and van der Waals bonding. In the former charge is transferred between atoms and in the latter there is no such transfer. Instead the electrons which form the bond never quite get completely transferred between the atoms, but spend much of their time in between the two nuclei. The positively charged nuclei are both attracted to the electrons which are interposed between them, but feel some net repulsion from each other as well. The mean atomic separation is of course set by the balance between these forces.
You might think that the covalent bond force was a power law somewhere between being proportional to 1/r2 and 1/r7. In fact the partial transfer of charge can only be explained quantum mechanically and when the calculations are done, a simple power law dependence for the force is never found.
Another, common bonding force which can only be explained in terms of quantum mechanics is the hydrogen bond, where a hydrogen atom interposes itself between two atoms or ions, e.g. HF2.
Finally, we should mention the so called steric forces of repulsion between atoms. You should notice that our description of the van der Waals force would predict attraction between all atoms. Yet we know that at least at small separation there is very strong repulsion. We think of this as describing the steric size of an atom or molecule. This strong steric repulsion arises because of the Pauli exclusion principle, a quantum mechanical law, which states that two electrons may not occupy the same quantum state.
2.3.6 Models of Interatomic and Intermolecular Forces
We often wish to predict the behaviour of atomic and molecular systems where the interactions are too complex to calculate directly from fundamental principles. In such cases we fall back on heuristic models of atomic and molecular interactions.
The best known of these models is due to Lennard and Jones, which is almost always used to describe systems with a force of attraction which is given by the van der Waals interaction. In this case the net force is given by
(2.3.11)
where r0 is the equilibrium separation (F(r0) = 0) and ε is related to the strength of the interaction. The first term in the brackets is the attractive component to the net force, i.e. the van der Waals attraction, and the second is the hard core repulsion. The vector êr is a radial unit vector pointing from the molecule exerting the force towards the molecule under consideration.
2.3.7 The Electrostatic Potential Energy and Potential
We begin our discussion of the potential energy in electrostatic fields by making a general definition of work. We define, dW, the work done in moving a particle a small distance ds under the application of a force F by
(SI units of Joules
(J) = Nm) (2.3.12)
where the angle θ is indicated in figure 2.3.9. This definition makes intuitive sense, since the work is clearly proportional to the force and the distance moved, but also if the force does not act in the direction of motion no work has been done. A neater way of expressing this, which retains the vectorial nature of the force and displacement, is to use the vector dot product
(2.3.13).
Figure 2.3.9. Defining the work done in moving a particle.
Let us now look at the work done in moving a particle of charge q around in the electrostatic field of a point charge, Q.
(2.3.14).
Now since êr is a radial vector only the component of motion which is also
radial will result in any work, figure 2.3.10. This means that the work done depends only on radial displacements, dr, in this electrostatic field.
(2.3.15).
To determine the total work done to get from a radial distance r1 to r2 we simply sum up all increments dr, i.e. we integrate the expression above.
(2.3.16).
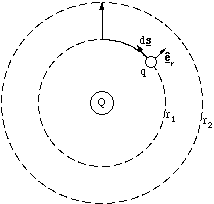
Figure 2.3.10. In following the the path indicated by the heavy line, only for the section from radius r1 to r2 is any work done, since along the circumference of r1 the force and displacement are always perpendicular.
As we would anticipate, this integral depends only on the endpoints of path we take, any route we choose will take an equivalent amount of work. The route shown in figure 2.3.10 is only one of an inifinite set which begins and ends at the points shown, and all of them require equal amounts of work. Furthermore if we take any route which starts and ends at the same position the total work done is zero. This property characterises a conservative field.In fact it can be shown that because electrostatic field lines do not cross, all electrostatic fields are conservative. It therefore makes sense to define a new scalar quantity, the electrostatic potential energy, U, which has well defined values in every region of space. By convention this is the negative of the work. For the point charge
(2.3.17)
All potential energy measurements must be made relative to another (U2 - U1) and we conventionally choose to set the potential energy to zero at infinite separation, hence
(2.3.18).
By analogy with the field we also define the potential V(r) for a point charge Q
(SI units of Volts
(V) = JC-1) (2.3.19).
Now we can plot the potential as a function of radial distance, figure 2.3.11. Here we have determined the potential for Q = -1.6x10-19 C. Since the test charge we use in determining V is defined to be positive we see that an attractive interaction is represented by a potential "well".
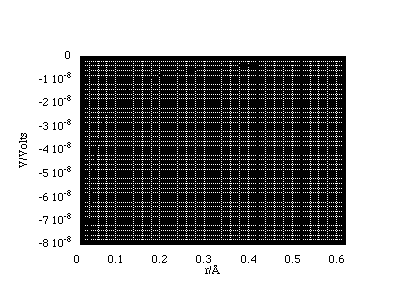Figure 2.3.11.
The potential for a point charge Q = -1.6x10-19 C.
Of course the potential is a spherically symmetric function (the potential has the same value on the surface of a sphere whose origin lies at the position of the point charge Q), so we have plotted a contour map of lines of equal potential in a plane intersecting the point charge, Figure 2.3.12. This contour plot should be read just like an ordinary map, each contour is plotted at equal increments in V and the darker the shading the more negative the value of V.
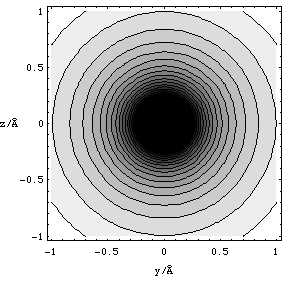
Figure 2.3.12. The plot of equipotential contours for point charge Q = -1.6x10-19 C in the y-z plane, with the charge at x=y=z=0.
If we wish to determine the potential from a dipole all we need to do is add
the potential from a positive and a negative charge, placed a distance 2l apart,
together. If we use Cartesian coordinates, and place the positive charge, +q,
at 
and the negative
charge, -q, at 
then the
potential is given by
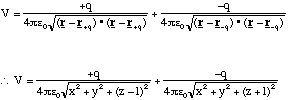(2.3.20).
We have plotted this as a contour plot in figure 2.3.13. A three dimensional representation of the dipole potential landscape in the y-z plane has been plotted in figure 2.3.14.
We can make a number of observations about the equipotential contour plot for the dipole. It is clear that the line bisecting the dipole momentum vector is also a line of equipotential, and that by symmetry this most be the equipotential line where V = 0. From our definition of V we have the following relationship between the field and the potential,
(2.3.21)
which indicates that the vector field can be recovered by finding the negative of the gradient of the potential. The gradient of the potential is simply the steepest slope at the point of interest on the potential surface. This gives the gradient of V both a magnitude and a direction, which is of course -E. The direction of the field lines for the dipole can quite easily be determined for the plane shown in figure 2.3.13, when it is appreciated that the steepest gradient must always be perpendicular to the equipotential contours (think of the contours on an Ordinance Survey map).
Figure 2.3.13. The equipotential contour plot for a dipole with 2l = 1.4Å, q = 1.6x10-19 C, plotted in the y-z plane with x = 0 (for code see "Physical Chemistry:Molecular Interactions: Dipole potential").
This recovery of the field from the potential map (which is normally quite straightforward to calculate) is a general property and leads to the following conclusion.
The potential (or potential energy) also allow one to visualize a landscape which is directly related to the field (or force). A positive charge (which the conventional definition of the field states is the test charge) can then be imagined to be a marble moving on the potential surface. Clearly the marble will fall into the "holes" created by negative point charges, whereas a positive point charge will look like a hill and will repel the positive test charge.
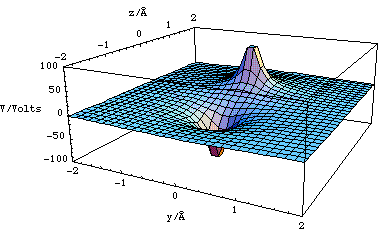
Figure 2.3.14. The potential surface for a dipole with 2l = 1.4Å, q = 1.6x10-19 C, plotted in the y-z plane with x = 0 (for code see "Physical Chemistry:Molecular Interactions: Dipole potential").
2.4 The Conservation of Energy
Energy is what has to be paid to do work. Energy comes in a variety of currencies and physical processes represent the conversion from one currency to another. Now this is not a definition, but it gives a flavour of what we conceive energy to be. It is a strangely wishy washy concept, but as the Physicist Kramers said
"The most important and most fruitful concepts are those to which it is impossible to attach a well defined meaning."
The value of energy as an idea, is the hypothesis that it is always conserved. It is transformed, but never lost. It is the single most important idea in thermodynamics, and probably the most powerful tool in the quantitative sciences. Curiously Newton never mentioned it!
2.4.1 The Kinetic Energy
It is implicit in what we have already done that energy is conserved in an electrostatic field, since the total work done if we take a path starting and finishing at the same point is zero. If energy was being dissipated this would not be the case.
However, we would like to know what energy is being traded if the path we take is not a loop. We do this by determining the "integral of motion" in the field. Here we consider a particle of charge q moving in the field of a particle of charge Q, along a radial direction between a radial distance r1 and r2.
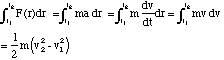(2.4.1)
where 1/2 mv2 is called the kinetic energy of the particle and v1 is the speed at r1 and v2 is the speed at r2. Now if no energy has been dissipated, we can equate this to the difference in potential energy between these points
(2.4.1)
and find that the sum of the kinetic energy, K, and the potential energy, U, must be a constant.
(2.4.2).
So this means that the total energy of the particle is constant, kinetic energy and potential energy are traded and we can start making predictions about the dynamic behaviour of charged particles in fields.
2.4.2 Molecular Dissociation
The simplest reaction we can study using the conservation of energy is the dissociation of a diatomic molecule. In our case let us model the dissociation of the dipolar diatomic molecule, NaCl. In NaCl the bonding is almost entirely ionic, so we already have an expression, (2.3.18), for the attractive interaction term between the ions. However, we do not have an expression for the stabilizing repulsion. The reason for this is that the repulsion is largely due to quantum mechanical effects as the ions overlap. Theory would suggest an exponential repulsive force exp(-kr), where k is a constant and r is the radial distance. Unfortunately this expression is mathematically inconvenient and in fact calculations are rather insensitive to the repulsive term, as long as it is quite steep. In the tradition of much Physical Chemistry we therefore model the repulsive interaction as a function of inter atomic separation, r, as V [[proportional]] 1/r9 (see [[section]] 2.3.5 and 2.3.6). The total potential energy then has the form
(2.4.3)
where A and B are constants. A of course is known, but B is not. To find B we determine the equilibrium separation r0 using the fact that dU/dr = 0 at this position.
(2.4.4).
Hence we find B to be
(2.4.5).
So we can re-express (2.4.3) in terms of r0 and electrostatic terms
(2.4.6)
and with r0 = 2.5 Å for a NaCl molecule we find the potential energy as a function of distance, figure 2.4.1.
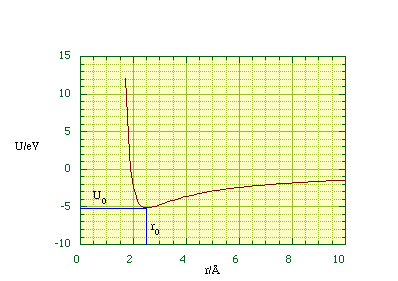
Figure 2.4.1. The potential energy function of an NaCl molecule.
The energy needed to pull the Na+ and Cl- ions apart is the difference in the potential energy at infinite separation and at equilibrium. Since U at infinity is by definition zero the dissociation energy is simply -U(r0) = 8.2 x 10-19 J (5.1 eV) which is within four percent of the experimentally measured value.
In this calculation we have assumed that at infinite separation the potential energy is zero, and so is the kinetic energy. That is, we just put enough initial kinetic energy in to the system to break the bond. Since the total energy is conserved before and after the reaction, and we assume no other energy losses or gains, the initial total energy must also be zero, i.e. Ki = -U(r0).
So the total initial kinetic energy is 8.2 x 10-19 J, but this is shared between two ions. To find out in what proportion we use the conservation of momentum. To break the bond the ions must move apart in exactly opposite directions (any motion not in this direction does not contribute to bond breaking). Since we assume the molecule to be at equilibrium the initial momentum is zero and hence so is the final momentum. Therefore the conservation of momentum gives us
(2.4.7)
and the conservation of energy gives us
(2.4.8).
Substituting into (2.4.8) from (2.4.7) we find
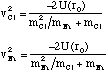(2.4.9).
Hence vCl = 2.7 kms-1 and vNa = 8.2 kms-1 and it is clear from (2.4.9) that the initial kinetic energies are not equal (KCl = 2.0 x 10-19 J and KNa = 6.2 x 10-19 J).
2.4.3 Can Reactions Occur?
Let us imagine a large container holding a single dissociated NaCl molecule, i.e. U = 0 and K >= 0. Now consider what will happen as time elapses. One might be tempted to say that the Na+ and Cl- ion will eventually meet as they bounce around inside the box and when they do they will react to form NaCl.
In the light of the discussion in [[section]]2.4.2 we can see that this is in fact entirely fallacious. The total energy of the system of 2 particles is greater than or equal to the binding energy, so it is impossible for any reaction to occur. The problem we have is that we need to carry off the excess energy from the two particles as they react. To do this we need a third body. A simple example would be if we had one KCl molecule and a single Na+ ion in our box. Now when the ion collides with the molecule it can react, because the excess kinetic energy can be transferred to the liberated K+ ion. Even here we can see that if we wait long enough another collision will occur and the reaction may reverse. It seems that the only way we can ensure the reaction has come to completion is to ensure that the excess energy actually escapes from the box!
So we are left with the interesting result that chemical reactions will not occur unless we have some way of wasting energy, and to do this in practice we require large numbers of particles so that three body collisions can occur.