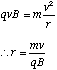This course introduces a number of fundamental physical principles which are used to predict, describe and analyse the behaviour of molecular systems.
Course Objectives
By the completion of the course you should be able to:
Key Concepts
Forces, fields, potential energy, potential, conservation of linear and angular momentum, conservation of energy.
Important Dates
Chemistry test - Friday 12th January 1996, 2 - 4.45 pm.
Physical Chemistry examination - provisionally Monday 17th June, am.Course Outline
"The Principles of Physics", Frank J. Blatt, 3rd edition, Allyn and Bacon.
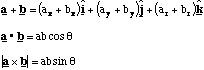
Cartesian Coordinates: Cylindical Coordinates:
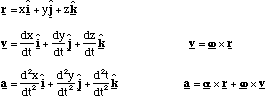
Linear (constant a):
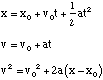
Rotational (constant α)
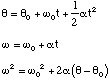
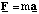
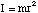

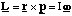
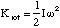
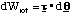
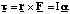

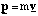
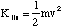
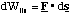
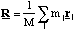
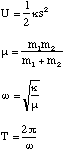
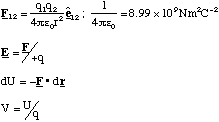
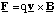
Question
Answer part (a) and EITHER (b) OR (c). If you answer both (b) and (c) only the first one you have answered will be marked.
(a) Shown below is a graph of the potential energy, U, as a function of interatomic separation, r, of two, different homonuclear diatomic molecules, X2 and Y2.
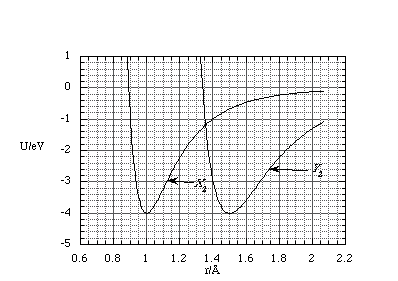
(i) What is the equilibrium separation of the atoms in X2?
[2 marks]
(ii) For what range of separations is the force between the atoms in X2 repulsive?
[2 marks]
(iii) What is the minimum energy needed to dissociate the molecule X2?
[2 marks]
(iv) If a photon with energy 6 eV is absorbed by the molecule X2, what is the final kinetic energy of each atom? You should assume that the molecule is at rest, i.e. it is not vibrating or rotating. State any further assumptions you have made.
[5 marks]
(v) Which molecule has the greater bond stiffness for small perturbations from equilibrium? Give a brief (1 paragraph) explanation of your reasoning.
[4 marks]
(b) A hydrogen atom travelling with initial velocity uî strikes a hydrogen molecule which is at rest, as shown below. After it has struck, the molecule has a velocity vî and the atom is at rest
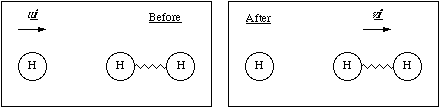
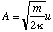
where κ is the bond stiffness of the hydrogen molecule.
[7 marks]
(c) An ion of charge q and mass m travels in a region of uniform magnetic field B. With B perpendicular to v, where v is the velocity vector of the ion, explain why the ion will follow a circular path and derive an expression, involving the variables referred to above, for the radius of the circular path.
[7 marks]
Answers
(a) (i) Equilibrium separation of the atoms X occur where the potential energy is at a minimum. Measuring from the graph this gives an equilibrium separation of 1Å.
(ii) The force is given by the negative of the gradient of the potential energy, i.e. dU = -F.dr, hence the interatomic force is repulsive wherever the gradient of U is positive. From the graph this is true for r < 1Å, and r cannot be less than 0Å.
(iii) The minimum dissociation energy can be found if we assume that at infinite separation the H atoms have zero kinetic energy (this can only occur if they separated by moving in exactly opposite directions). Then the dissociation energy is simply the difference in potential energy at equilibrium and as r tends to infinity. From the graph this means the dissociation energy is 4eV.
(iv) If we assume that the photon is absorbed and causes the atoms to fly apart in opposite directions, as in (iii), then the excess kinetic energy is 2eV. Since the molecule is homonuclear each X has the same mass and by the conservation of momentum each must carry equal but opposite momentum, i.e. they have the same kinetic energy. The kinetic energy is therefore 1eV for each atom.
In fact the photon has a momentum given by the de Broglie relationship, p = h/λ, which must be conserved after the absorption. This gives the molecule, initially at rest, a very small component of velocity in the direction of the photon's flight path and this may result in a small difference in the kinetic energy of each atom. For example if the atoms dissociate along the same line as the photon followed the one travelling in the same direction as the photon will have slightly more kinetic energy than the one travelling in the opposite direction.
(v) The bond stiffness of X2 is greater than that of Y2. This can be seen if we consider a small extension / compression about equilibrium. For the same displacement the potential energy in X2 has risen by a greater amount than Y2 and hence the energetic cost for a small displacement is greater, i.e. the bond is stiffer.
(b) The hydrogen atom travelling at velocity uî has a kinetic energy
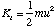
where m is the mass of a hydrogen atom. Since there is no interaction potential between atom and molecule and the molecule is at rest, the initial energy of the system is simply this kinetic energy. Subsequently the atom is at rest and the molecule has a linear velocity vî giving it a kinetic energy of
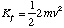
The energy taken up in the molecule's oscillations is given by the difference in the initial and final kinetic energy of the system. We can find this by determining v in terms of u by conservation of linear momentum
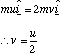
and then total energy of the oscillations, Eosc is given by
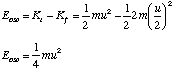
To find the amplitude, A, of the oscillations we simply note that during simple harmonic motion the kinetic energy is zero when the molecule is at its maximum and minimum extension and that the potential energy is at this point given by

which after re-arrangement gives

and hence
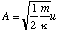
as required.
(c) The force, F, acting on the ion is the Lorentz force given by
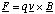
This means that the force always acts at right angles to the plane defined by the instantaneous velocity and magnetic field vectors. Since the force is always perpendicular to the direction of motion, the magnitude of the velocity cannot be altered (no work is being done since F.ds = 0 in this case). By definition this means that the motion must be circular and the acceleration on the particle is centripetal.
Hence we can equate the magnitude of the Lorentz force to the product of the centripetal acceleration and the particle's mass, m.