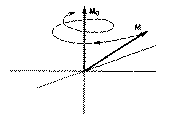
A collection of spin 1/2 nuclei (Protons) all with identical chemical environments.
A collection of
identical nuclei will all precess with the Larmor frequency but with
random phases relative to each other such that on average the overall
(macroscopic) magnetisation vector Mo remains along the z axis
(a).

Imagine now
some electromagnetic energy (in the radio-frequency region of the spectrum)
produced by an oscillator (transmitter) and continuously applied to
this system in such a way that its magnetic component B1 is orientated
along the x axis, ie perpendicular to the applied magnetic field. If
this electromagnetic field has a specific oscillation frequency, this can be
resolved into two rotational components +w and -w with
respect to the z axis. If we adjust things such that +w of the
applied field matches the Larmor frequency wo exactly, it
is said to be in resonance with the precession of our group of
protons. Two things can be thought of as happening when this resonance
occurs;
- The resonance provides the energy to "flip" some of the
proton nuclei from the ground to the excited state
- energy can only be
transferred to any individual precessing proton if its relative phase is the
same as that of +w, ie the precession of the magnetisation vectors
becomes coherent.
If the phases of a proportion of the
precessing protons are coherent, the individual magnetisation vectors no
longer cancel each other (b above). Instead the overall macroscopic
vector "tips" away from Mo to a new value M by some angle
q (defined later in eqn 6) with respect to the z axis. Because
the population in the ground (spin +1/2) state is very slightly greater than
the opposing state, M is shown as a positive component in the z axis
in the diagram above. The new magnetisation vector M now precesses
about about the z axis and produces a new non-zero magnetisation
component in the xy plane which did not exist before B1 was
applied. Note that if M tips away from Mo by an angle q of
90, the populations of the ground (M) and the excited (-M) states become
equalised. If the angle q is 180, the populations effectively invert,
ie there is a slight preponderance of the excited state. At this
point, it is not possible for the nuclei to absorb any more energy. There are
however several mechanisms whereby the nuclei can loose energy, or
relax. The first involves transfer of energy from the nucleus to
surrounding molecules as thermal motion (heat) by a process known as
spin-lattice or longitudinal relaxation (see below) and the second involves
energy transfer to nuclei of a different type (ie with a different
chemical shift) referred to as spin-spin or transverse relaxation. The
rate of relaxation is exponential and is defined by time constants
called T1 and T2 respectively (for protons these have values of ca 0.2
- 5 seconds).
This relaxation phenomenon will have implications for the "width" of
the subsequent spectral lines we will measure (see later).
We are
now in a position to measure experimentally the frequency of the process
leading to the non-zero magnetisation
component in the xy plane which did not exist before B1 was
applied. This is done by placing a coil
(receiver) along the y axis of our coordinate system and
measuring the y component magnetisation of the precessing vector
M. When resonance occurs, the oscillating current induced in the
receiver is detected, amplified and displayed as an "NMR signal". Note
particularly that we measure only the xy component magnetisation of
M, and NOT absorption or emission of energy by the protons. [Actually,
we could measure the excited state relaxation by microcalorimetry, ie
the solution warms up slightly when resonance occurs!].
Return to Index page
Copyright (c) H. S. Rzepa and ICSTM Chemistry Department, 1994, 1995.


