Principles of NMR.

The nuclei of all elements carry a charge. When the spins of the protons and neutrons comprising these nuclei are not paired, the overall spin of the charged nucleus generates a magnetic dipole along the spin axis, and the intrinsic magnitude of this dipole is a fundamental nuclear property called the nuclear magnetic moment, µ. The symmetry of the charge distribution in the nucleus is a function of its internal structure and if this is spherical (ie analogous to the symmetry of a 1s hydrogen orbital), it is said to have a corresponding spin angular momentum number of I=1/2, of which examples are 1H, 13C, 15N, 19F, 31P etc. Nuclei which have a non-spherical charge distribution (analogous to e.g. a hydrogen 3d orbital) have higher spin numbers (eg 10B, 14N etc) outside the scope of this particular lecture course. 

In quantum mechanical terms, the nuclear magnetic moment of a nucleus can align with an externally applied magnetic field of strength Bo in only 2I+1 ways, either re-inforcing or opposing Bo. The energetically preferred orientation has the magnetic moment aligned parallel with the applied field (spin +1/2) and is often given the notation a, whereas the higher energy anti-parallel orientation (spin -1/2) is referred to as b. 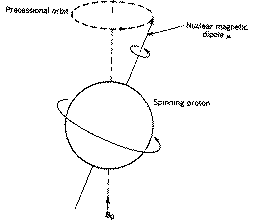The rotational axis of the spinning nucleus cannot be orientated exactly parallel (or anti-parallel) with the direction of the applied field Bo (defined in our coordinate system as about the z axis) but must precess about this field at an angle (for protons about 54š) with an angular velocity given by the expression;

wo = gBo ...(1) (the Larmor frequency, in Hz) 

The constant g is called the magnetogyric ratio and relates the magnetic moment m and the spin number I for any specific nucleus;

g = 2pm/hI ...(2) (h is Planck's constant) 


For a single nucleus with I=1/2 and positive g, only one transition is possible (D I=1, a single quantum transition) between the two energy levels; 



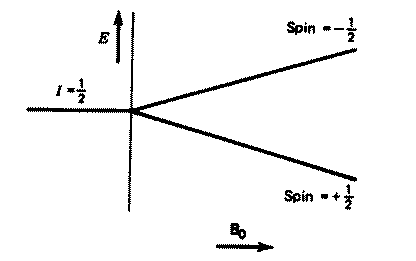
NMR is all about how to interpret such transitions in terms of chemical structure. We will first consider the energy of a typical NMR transition. If angular velocity is related to frequency by wo = 2¼n, then

n = gBo/2¼ ...(3) 

It follows that proton NMR transitions (DI=1) have the following energy; 

hn = DE = hgBo./2p ...(4) 

For a proton g = 26.75 x 107 rad T-1 s-1 and Bo ~ 2T, DE = 6 x 10-26 J. The relative populations of the higher (n2) and lower (n1) energy levels at room temperature are given by the Boltzmann law;

n2/n1 = e-DE/kT ~ 0.99999. ...(5) 

For NMR, this means that the probability of observing a transition from n1 to n2 is only slightly greater than that for a downward transition, ie the overall probability of observing absorption of energy is quite small. This relationship also explains why a larger Bo favours sensitivity in NMR measurements, increasing as it does the difference between the two Boltzmann levels, and why NMR becomes more sensitive at lower temperatures.