Practical Aspects.

To obtain good spectra free from too much electronic noise, it is common to add together between 8 - 800 FIDs, a process which takes between ~30 seconds to 24 hours. Over that sort of period the field frequency may drift slightly, resulting in poor averaging. To compensate for this, most FT spectrometers have special "lock circuitry" based on detecting a deuterium signal. For this to work, the solvent used MUST contain deuterium! Normally CDCl3 is used, but deuterated acetone or DMSO are also common, and "locking" the sample is normally the first operation actually performed on the spectrometer, and further the "lock signal" is also used to "shim" the spectrometer, ie adjust the homogeneity of Bo. Note that carbon tetrachloride should not be used as a solvent for this reason.

At the end of the short radio frequency pulse tp, the precession of all the nuclei in the magnetic field was effectively in phase. Provided measurement of the resultant induced signal in the y axis starts immediately afterwards, all the initial measured sine wave responses would also be in phase. However, no NMR spectrometer yet constructed can achieve this and for electronic reasons, a short delay between the end of t_p and start of measurement is required. The short delay means measurement begins when the sine waves are already out of phase. This so called first order phase error can be calculated from a suitable combination of the real and imaginary components of F(). Another phasing error due to technical imperfections in the spectrometer is often referred to as the zero order phase correction. These are both applied to F() after the FT is complete.

With the measurement of a single FID resulting from one pulse, followed by Fourier Transformation to give F(), one can achieve a spectrum approximately equivalent in its noise level to a CW spectrum which took 600 or more seconds to record! By adding n FID measurements together in the computer, one can reduce the noise by ˆn, ie 64 FIDs added together (and taking 3.41*64= 3.6 minutes) will reduce the noise by almost a factor of 10. It also turns out that one can multiply the whole of f(t) by a new function such as a decaying exponential prior to the FT operation. Surprisingly, this does NOT introduce any new frequencies, but can dramatically reduce the noise level at the expense of making the resulting peaks broader. This is because a faster f(t) decay corresponds to a shorter relaxation time T, a larger 1/T, and hence wider peaks (cf 14N discussed in a later lecture course).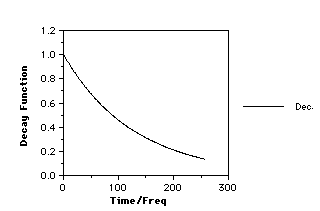

Other more complex functions (weighting functions) can actually decrease apparent peak width, this time at the expense of the noise level. The effects of such functions, as well as first order phase and non-Nyquist sampling errors etc are readily demonstrated using a relatively short computer program. Such a program is in fact described as one of the Fortran programming course projects, the output of which is shown below;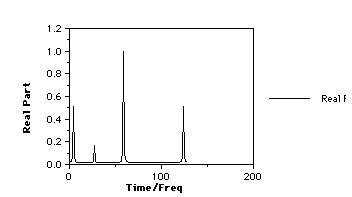

Summary

We have set out how a short pulse of electromagnetic radio frequency radiation can establish a resonance with precessing nuclei in an applied magnetic field, and in doing so establish a coherent phased precession which effectively tilts the precessing magnetisation vector away from the axis of the applied field by a certain angle called the pulse angle. This induces a response in a detector which is measured as a function of time and can be converted to a more readily interpreted frequency domain signal by digitisation and Fourier Transformation. A whole range of more sophisticated experiments can be derived from this simple one by varying the pulse angle, adding extra pulses and inserting time delays, the entire assemblage being called a pulse sequence. Description of these experiments is beyond the present scope of the lectures, but some will be described in third year lectures.

---