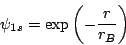The H atom

In this section you will calculate the wavefunction of an H atom by loading a CRYSTAL input file: H.inp

Starting DLVisualize

Open a terminal - right mouse click on the background, select Open Terminal
In the terminal run the command source /opt/chemistry/crystal/elec_str_setup
This sets up the environment you need to use DLViz
type dlv to start DLViz

Exercise 1: Run a CRYSTAL calculation:

Calculate->CRYSTAL->Run SCF Input file
Click on Browse
Select H.inp
Select OK
Select OK

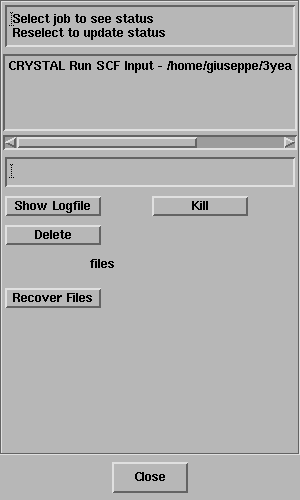
The Job List panel will open automatically and look something like this;

Select the job and the status line should report "Job has completed" - like this;

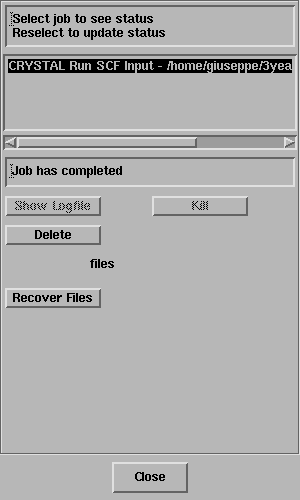
Click on Recover Files.

A model of H should have appeared in the DLV 3DView window.

Give the current model a suitable name. This will be used as the label for this model in subsequent CRYSTAL simulations.

Edit -> Model -> Name
Change "Model_1" to something suitable; say "H atom".

Note:

For the change to take effect you must press Return.
You'll see the name of the graphics window change to "DLV 3DView - H atom";

A second window will open displaying the output from the CRYSTAL calculation (the LogFile).

It should look something like H.out

Take some time to read through the output in order to answer to the following questions.

Questions:

What is the hamiltonian/method adopted in the calculation?
What is the energy of the hydrogen atom in Hartree?
In the output, the energy is given in atomic unit (Hartree).
Convert the energy in eV, in J and kcal/mol.
Compare this energy with the energy of the hydrogen atom.
What is the energy of the atomic orbital?
Hints: Look for the string "ORBITAL ENERGIES" in the output.

Optional questions::

What is the meaning of "minimal basis set"?
Are you using a "minimal basis set" in your calculation?
Plot the combination of gaussians given in the output?
Hints: Look for the string "NO. TYPE EXPONENT S COEF" in the output.
The exponent unit is Bohr²: 1 Bohr = 0.5291772083 Angstrom = a₀ = r_B
Compare the plotted atomic orbital with the exact 1s atomic orbital
obtained by solving analytically the Schoedinger's equation for the hydrogen atom:

$\begin{displaymath} \psi = \exp{\left(-\frac{r}{r_B} \right)} \end{displaymath}$

Is the contraction (combination) of gaussians able to describe the exponential decrease
of the amplitude of probability to find the electron at any points?