The H crystal
A cell with only a hydrogen atom
repeated by translation in three directions
will be considered.
The cell is described by six lattice parameters:
three lattice vectors,
a, b and c, and three angles
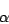 (between b and c),
(between b and c),
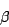 (between a and c) and
(between a and c) and
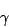 (between a and b);
in this case a=b=c
and all the angles are
(between a and b);
in this case a=b=c
and all the angles are
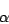 =
=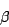 =
=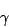 =90º.
=90º.
The infinite number of electronic states, that form a continuum in
energy, are grouped together in a band.
Each level in a band is labelled by a vector
k=(kx,ky,kz).
The quantity k belongs to a space called,
the reciprocal space; in this space a three dimentional cell
can be also defined, the reciprocal cell, and it is
useful and convenient, as the system is also periodic in
the reciprocal space.
The reciprocal lattice parameters a*, b*
and c*
are related to the lattice parameters of the cell in direct space
according to the following formula:
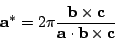
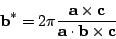
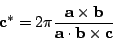 .
.
In this section you will calculate the wavefunction
and the band structure
for the hydrogen crystal.
Exercise 1: Start DLVisualize,
run a CRYSTAL calculation for the H crystal:
H_crystal.inp
Exercise 2: Run a CRYSTAL properties calculation
of the band structure for the H crystal.
In the CRYSTAL Bands panel,
note that the coordinates are expressed in unit of a*,
b* and c*.
Questions:
- How many atoms are there in the cell?
Look also the the output from the CRYSTAL
calculation (the LogFile).
- How many bands are visualised in the band structure?
- Where are the bonding and anti-bonding states?
Is there any non-bonding state?
Index
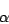 (between b and c),
(between b and c),
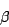 (between a and c) and
(between a and c) and
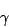 (between a and b);
in this case a=b=c
and all the angles are
(between a and b);
in this case a=b=c
and all the angles are
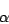 =
=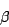 =
=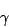 =90º.
=90º.
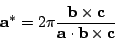
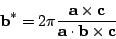
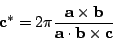 .
.