In this section you will calculate the wavefunction of a H2 molecule by loading a CRYSTAL input file: H2.inp
Exercise 1: Start DLVisualize and run a CRYSTAL calculation:
Calculate->CRYSTAL->Run SCF Input file
Click on Browse
Select H2.inp
Select OK
Select OK
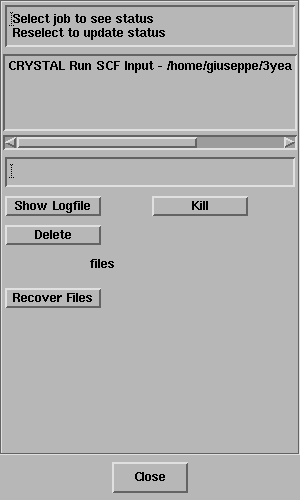
The Job List panel will open automatically and look something like this;

Select the job and the status line should
report "Job has completed" - like this;
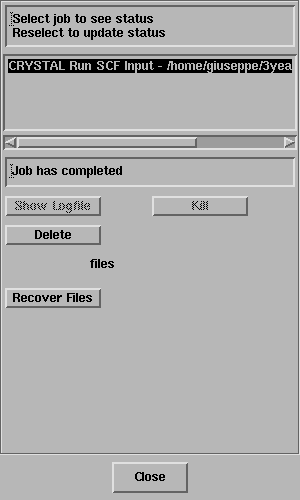
Click on Recover Files.
A model of H2 should have appeared in the DLV 3DView window.
On main panel the square icons are toggles which control how the 3D structure is displayed. A help message is displayed when you pass the mouse over each button. At first you are in rotate mode and can spin the structure by dragging with the right mouse button. Try changing to scale mode and translate mode etc.
Open the Structure Display panel
Display->Structure
Try out the controls on this panel - you can change the size of the atoms, display bonds etc etc.
Give the current model a suitable name. This will be used as the
label for this model in subsequent CRYSTAL simulations.
Edit -> Model -> Name
Change "Model_1" to something suitable; say "H2".
Note:
For the change to take effect you must press Return.
You'll see the name of the graphics window change to "DLV 3DView - H2";
In the DLV 3DView window, if the two hydrogen atoms are selected
(just left-click on them), the H-H distance will appear in the main window.
A second window will open displaying the output from the CRYSTAL calculation (the LogFile).
It should look something like H2.out
Take some time to read through the output in order to answer to the following questions.